カルマンフィルタ、状態推定装置、カルマンフィルタの制御方法、及びカルマンフィルタの制御プログラム
【課題】カルマンフィルタの計算量を低減する
【解決手段】カルマンフィルタKFは、姿勢q+k−1及びベクトルβ+k−1を要素とする状態ベクトルx+k−1を、状態遷移モデルに適用して、姿勢q−k及びベクトルβ−kを要素とする状態ベクトルx−kを算出する推定状態ベクトル算出部140と、状態ベクトルx−kの推定誤差の共分散P−kを算出する共分散算出部125とを備える。推定状態ベクトル算出部は、ベクトルβ−kをベクトルβ+k−1と等しい値に設定し、共分散算出部125は、共分散P−kのうち、ベクトルβ−kの推定誤差の共分散を表す成分P−ββ,kを、状態ベクトルx+k−1の推定誤差の共分散P+k−1のうち、ベクトルβ+k−1の推定誤差の共分散を表す成分P+ββ,k−1、及び、状態遷移モデルのプロセスノイズの共分散(Qk)のうち、ベクトルβ+k−1のプロセスノイズの共分散を表す成分Qββの和として算出する。
【解決手段】カルマンフィルタKFは、姿勢q+k−1及びベクトルβ+k−1を要素とする状態ベクトルx+k−1を、状態遷移モデルに適用して、姿勢q−k及びベクトルβ−kを要素とする状態ベクトルx−kを算出する推定状態ベクトル算出部140と、状態ベクトルx−kの推定誤差の共分散P−kを算出する共分散算出部125とを備える。推定状態ベクトル算出部は、ベクトルβ−kをベクトルβ+k−1と等しい値に設定し、共分散算出部125は、共分散P−kのうち、ベクトルβ−kの推定誤差の共分散を表す成分P−ββ,kを、状態ベクトルx+k−1の推定誤差の共分散P+k−1のうち、ベクトルβ+k−1の推定誤差の共分散を表す成分P+ββ,k−1、及び、状態遷移モデルのプロセスノイズの共分散(Qk)のうち、ベクトルβ+k−1のプロセスノイズの共分散を表す成分Qββの和として算出する。
【発明の詳細な説明】
【技術分野】
【0001】
本発明は、カルマンフィルタ、状態推定装置、カルマンフィルタの制御方法、及びカルマンフィルタの制御プログラムに関する。
【背景技術】
【0002】
近年、携帯機器の高性能化及び多用途化に伴い、地磁気の方向や携帯機器の姿勢等の推定機能を備える携帯機器の研究開発が盛んに行われている。地磁気の方向や携帯機器の姿勢等を推定する場合、地磁気センサ等の単体のセンサからの出力のみを利用して推定するよりも、異種の物理量を測定する複数のセンサからの出力を統合して推定する方が、より高速に正確な値を推定することができる。
【0003】
異種の物理量を測定する複数のセンサの出力を統合し、動的システムの状態を推定する方法として、拡張カルマンフィルタ(EKF)やシグマポイントカルマンフィルタ(SPKF)等の非線形カルマンフィルタを用いる方法が知られている。
例えば、特許文献1には、3軸の角速度センサ及び3軸の加速度センサと非線形カルマンフィルタとを実装した姿勢角計測装置が開示されている。また、非特許文献1には、3軸角速度センサ、3軸加速度センサ、及び3軸地磁気センサからの出力信号を、アンセンテッド変換を用いたシグマポイントカルマンフィルタによって統合し、姿勢を推定する方法が開示されている。シグマポイントカルマンフィルタは、他のカルマンフィルタに比べて、非線形システムのモデル化に適した演算方法であり、シグマポイントカルマンフィルタを用いることで、非線形な動的システムの状態を正確に推定することができる。
【先行技術文献】
【特許文献】
【0004】
【特許文献1】特開平9−5104号公報
【非特許文献】
【0005】
【非特許文献1】Wolfgang Gunthner, “Enhancing Cognitive Assistance Systems with Inertial Measurement Units”, Springer, 2008
【発明の概要】
【発明が解決しようとする課題】
【0006】
しかし、シグマポイントカルマンフィルタによる演算は計算量が多いため、シグマポイントカルマンフィルタが実装される機器には、大容量のメモリと高性能のCPUとを備えることが必要となる。そして、シグマポイントカルマンフィルタによる演算を行う場合、多くの電力が消費される。特に、シグマポイントカルマンフィルタを実装した機器が、バッテリーで給電される携帯機器の場合、機器の長時間使用が困難になるという課題が存在した。
本発明は、上述した点に鑑みてなされたものであり、シグマポイントカルマンフィルタの演算を簡素化し、高速且つ低消費電力な状態推定装置の実現を解決課題とする。
【課題を解決するための手段】
【0007】
以下、本発明について説明する。なお、本発明の理解を容易にするために本実施形態、変形例、及び添付図面の参照符号を括弧書きにて付記するが、それにより本発明が本実施形態に限定されるものではない。
【0008】
上記課題を解決するため、本発明に係るカルマンフィルタは、第1ベクトル(β+k−1)及び第2ベクトル(q+k−1)を要素とする状態ベクトル(x+k−1)と、前記状態ベクトルの推定誤差の共分散(P+k−1)と、に基づいて、状態遷移モデル(f)を用いて、推定第1ベクトル(β−k)及び推定第2ベクトル(q−k)を要素とする推定状態ベクトル(x−k)を算出する推定状態ベクトル算出部と、前記推定状態ベクトルの推定誤差の共分散(P−k)を算出する共分散算出部と、前記状態遷移モデル及び観測モデル(h)を用いて、前記状態ベクトルから、推定観測値ベクトル(y−k)を算出する推定観測値ベクトル算出部と、前記推定観測値ベクトルと、外部の複数のセンサから出力される観測値を要素とする観測値ベクトル(yk)とに基づいて、観測残差(ek)を算出する観測残差生成部と、前記観測残差と、前記推定状態ベクトルとに基づいて、前記状態ベクトルを更新したベクトルを算出する更新部と、を備え、前記推定状態ベクトル算出部は、前記推定第1ベクトルを、前記第1ベクトルと等しい値に設定し、前記共分散算出部は、前記状態ベクトルの推定誤差の共分散のうち、前記第1ベクトルの推定誤差の共分散を表す成分(P+ββ,k−1)、及び前記状態遷移モデルにおいて前記状態ベクトルに生じるプロセスノイズの共分散のうち、前記第1ベクトルに生じるプロセスノイズの共分散を表す成分(Qββ)を加算して、前記推定状態ベクトルの推定誤差の共分散のうち、前記推定第1ベクトルの推定誤差の共分散を表す成分(P−ββ,k)を算出する、ことを特徴とする。
【0009】
この発明によれば、共分散算出部は、推定状態ベクトルの推定誤差の共分散のうち推定第1ベクトルの推定誤差の共分散を表す成分を、2個の行列を加算することで算出する。
一般的に、あるベクトルの推定誤差の共分散は、まず、当該あるベクトルの推定誤差を表すベクトルを算出し、その後、推定誤差を表すベクトルと、推定誤差を表すベクトルを転置したベクトルとの積を算出することにより求められる。よって、あるベクトルの推定誤差の共分散を求めるためには、推定誤差を表すベクトルを算出する演算の他に、当該あるベクトルの次元を表す数の二乗に相当する回数の演算が必要になる。
シグマポイントカルマンフィルタは、複数のシグマポイントに基づいて、推定状態ベクトルの推定誤差を表すベクトルを複数生成し、生成した複数の推定誤差を表すベクトルを用いて、推定状態ベクトルの推定誤差の共分散を算出する。従って、推定状態ベクトルの推定誤差の共分散を求めるためには、推定状態ベクトルの次元を表す数の二乗に相当する回数の演算を、更に、シグマポイントの個数に相当する回数だけ繰り返すことが必要となる。このように、推定状態ベクトルの推定誤差の共分散を求める演算は、計算量が多く、シグマポイントカルマンフィルタの処理負荷を増大させる要因となっていた。
これに対して、この発明の共分散算出部は、推定状態ベクトルの推定誤差の共分散のうちの一部の成分を、2つの行列の加算という単純な演算により算出するため、従来の方法に従って計算した場合に比べて、推定状態ベクトルの推定誤差の共分散を求める演算に係る計算量の大幅な低減を可能とした。これにより、シグマポイントカルマンフィルタの演算の高速化と、シグマポイントカルマンフィルタの演算に必要な電力の低減が可能となった。
なお、この発明の推定状態ベクトル算出部は、推定第1ベクトルを第1ベクトルと等しい値に設定する。しかし、第1ベクトルは、カルマンフィルタの演算において、値を全く変化させない訳ではない。すなわち、推定第1ベクトルを要素として含む推定状態ベクトルは、更新部において観測残差による更新がなされ、カルマンフィルタの推定対象であるシステムの状態を正確に表す値(真値)へと更新される。これにより、この発明に係るカルマンフィルタは、システムの状態を正確に推定することができる。
【0010】
また、上述したカルマンフィルタにおいて、前記推定状態ベクトル算出部は、前記状態ベクトルと、前記状態ベクトルの推定誤差の共分散とに基づいて、複数のシグマポイント(χ+k−1)を生成するシグマポイント生成部と、前記状態遷移モデルを用いて、前記複数のシグマポイントから、複数の推定シグマポイント(χ−k)を算出する状態遷移モデル部と、前記推定状態ベクトル(x−k)を算出する平均算出部と、を備え、前記状態遷移モデル部は、前記推定シグマポイントのうち、前記推定第2ベクトル(q−k)を算出するために用いられる要素以外の要素を、前記シグマポイントのうち、前記第1ベクトル(β+k−1)に基づいて生成された要素と等しい値に設定し、前記平均算出部は、前記推定第1ベクトル(β−k)を、前記第1ベクトル(β+k−1)と等しい値に設定し、前記推定第2ベクトル(q−k)を、前記複数の推定シグマポイント(χ−k)に基づいて算出することが好ましい。
【0011】
この発明によれば、状態ベクトルの推定値を、複数のシグマポイントを用いて算出する。これにより、状態遷移モデルを用いた状態ベクトルの推定において、状態ベクトルが有する誤差による影響と、カルマンフィルタが推定対象とするシステムの非線形性による影響とを低減させることができ、状態遷移モデルにおける推定精度の低下を防止することができる。すなわち、この発明によれば、カルマンフィルタが、システムの状態を正確に推定することが可能となる。
また、この発明によれば、推定第1ベクトルを、第1ベクトルと等しい値に設定し、推定第2ベクトルのみを、複数の推定シグマポイントに基づいて算出するため、推定状態ベクトルの算出に係る計算負荷を低減させることが可能となる。
【0012】
次に、本発明に係る状態推定装置は、システムを観測して観測値を各々出力する複数のセンサと、上記のうちいずれかのカルマンフィルタとを備えることを特徴とする。
この発明によれば、高速なカルマンフィルタの演算が可能で、且つ低消費電力な状態推定装置が実現される。
【0013】
次に、本発明に係るカルマンフィルタの制御方法は、システムの状態を推定するカルマンフィルタの制御方法であって、第1ベクトル及び第2ベクトルを要素とする状態ベクトルと、前記状態ベクトルの推定誤差の共分散と、に基づいて、状態遷移モデルを用いて、推定第1ベクトル及び推定第2ベクトルを要素とする推定状態ベクトルを算出する工程と、前記推定状態ベクトルの推定誤差の共分散を算出する工程と、前記状態遷移モデル及び観測モデルを用いて、前記状態ベクトルから、推定観測値ベクトルを算出する工程と、前記推定観測値ベクトルと、外部の複数のセンサから出力される観測値を要素とする観測値ベクトルとに基づいて、観測残差を算出する工程と、前記観測残差と、前記推定状態ベクトルとに基づいて、前記状態ベクトルを更新したベクトルを算出する工程と、を備え、前記推定状態ベクトルを算出する工程は、前記推定第1ベクトルを、前記第1ベクトルと等しい値に設定し、前記推定状態ベクトルの推定誤差の共分散を算出する工程は、前記状態ベクトルの推定誤差の共分散のうち、前記第1ベクトルの推定誤差の共分散を表す成分、及び前記状態遷移モデルにおいて前記状態ベクトルに生じるプロセスノイズの共分散のうち、前記第1ベクトルに生じるプロセスノイズの共分散を表す成分を加算して、前記推定状態ベクトルの推定誤差の共分散のうち、前記推定第1ベクトルの推定誤差の共分散を表す成分を算出する、ことを特徴とする。
【0014】
この発明によれば、推定状態ベクトルの推定誤差の共分散を求める演算の計算量を、従来の方法に従って計算した場合に比べて大幅に低減することが可能となり、カルマンフィルタの演算の高速化と、カルマンフィルタの演算に必要な電力の低減が可能となった。
【0015】
次に、本発明に係るカルマンフィルタの制御プログラムは、システムの状態を推定するカルマンフィルタの制御プログラムであって、第1ベクトル及び第2ベクトルを要素とする状態ベクトルと、前記状態ベクトルの推定誤差の共分散と、に基づいて、状態遷移モデルを用いて、推定第1ベクトル及び推定第2ベクトルを要素とする推定状態ベクトルを算出する処理と、前記推定状態ベクトルの推定誤差の共分散を算出する処理と、前記状態遷移モデル及び観測モデルを用いて、前記状態ベクトルから、推定観測値ベクトルを算出する処理と、前記推定観測値ベクトルと、外部の複数のセンサから出力される観測値を要素とする観測値ベクトルとに基づいて、観測残差を算出する処理と、前記観測残差と、前記推定状態ベクトルとに基づいて、前記状態ベクトルを更新したベクトルを算出する処理と、をコンピュータに実行させ、前記推定状態ベクトルを算出する処理は、前記推定第1ベクトルを、前記第1ベクトルと等しい値に設定し、前記推定状態ベクトルの推定誤差の共分散を算出する処理は、前記状態ベクトルの推定誤差の共分散のうち、前記第1ベクトルの推定誤差の共分散を表す成分、及び前記状態遷移モデルにおいて前記状態ベクトルに生じるプロセスノイズの共分散のうち、前記第1ベクトルに生じるプロセスノイズの共分散を表す成分を加算して、前記推定状態ベクトルの推定誤差の共分散のうち、前記推定第1ベクトルの推定誤差の共分散を表す成分を算出する、ことを特徴とする。
【0016】
この発明によれば、推定状態ベクトルの推定誤差の共分散を求める演算の計算量を、従来の方法に従って計算した場合に比べて大幅に低減することが可能となり、カルマンフィルタの演算の高速化と、カルマンフィルタの演算に必要な電力の低減が可能となった。
【図面の簡単な説明】
【0017】
【図1】本発明の実施形態に係る携帯機器の構成を示すブロック図である。
【図2】携帯機器の外観を示す斜視図である。
【図3】本発明の実施形態に係るカルマンフィルタの機能ブロック図である。
【発明を実施するための形態】
【0018】
<A.実施形態>
本発明の実施の形態について図面を参照して説明する。
【0019】
[1. 機器構成及びソフトウェア構成]
図1は、本発明の実施形態に係る携帯機器のブロック図であり、図2は携帯機器の外観を示す斜視図である。携帯機器1は、携帯機器1の姿勢を変えることにより変化する画面の向く方向に応じて地図などの画像を回転させることによって、画像によって表される方位を、現実空間の方位に追従させる機能を備える。この機能は、各種センサの出力に基づいてカルマンフィルタの演算を行い、携帯機器1の姿勢等を推定することによって実現される。
【0020】
携帯機器1は、各種の構成要素とバスを介して接続され装置全体を制御するCPU10、CPU10の作業領域として機能するRAM20、各種のプログラムやデータを記憶したROM30、通信を実行する通信部40、画像を表示する表示部50、及びGPS部60を備える。GPS部60は、GPS衛星からの信号を受信して携帯機器1の位置情報(緯度、経度)を生成するものである。また、携帯機器1は、地磁気を検出して磁気データを出力する3次元磁気センサ70、加速度を検出して加速度データを出力する3次元加速度センサ80、及び角速度を検出して角速度データを出力する3次元角速度センサ90を備える。
【0021】
3次元磁気センサ70は、X軸磁気センサ71、Y軸磁気センサ72、及びZ軸磁気センサ73を備える。各センサは、MI素子(磁気インピーダンス素子)、MR素子(磁気抵抗効果素子)などを用いて構成することができる。磁気センサI/F74は、各センサからの出力信号をAD変換して磁気データmを出力する。この磁気データmは、x軸、y軸およびz軸の3成分によって表されるベクトルデータである。
【0022】
ところで、3次元磁気センサ70が搭載される携帯機器1は、着磁性を有する各種金属や、電気回路等、磁界を発生させる部品が備えられることが多い。このため、3次元磁気センサ70が出力する磁気データmは、磁極北に向かう水平成分と伏角方向の鉛直成分とを有する地磁気を表すベクトルの他に、機器に搭載された部品が発する磁界等を表すベクトルも含む値となる。従って、地磁気の値を正確に知るためには、3次元磁気センサが出力するベクトルデータ(磁気データm)から、携帯機器1の部品が発する内部磁界を表すベクトルを取り除く補正処理が必要となる。
このように、検出対象である地磁気の正確な値を得るために、補正処理において、3次元磁気センサ70から出力されるデータから取り除かれるべき内部磁界の値を3次元磁気センサ70のオフセットmOFFと呼ぶ。
なお、地磁気検出部70は、携帯機器1の外部にある外部物が発する磁界についても検出する。しかし、本実施形態では、外部物が発する磁界は無視できる程小さいものとする。
【0023】
3次元加速度センサ80は、X軸加速度センサ81、Y軸加速度センサ82、及びZ軸加速度センサ83を備える。各センサは、ピエゾ抵抗型、静電容量型、熱検知型などどのような検知方式であってもよい。加速度センサI/F84は、各センサからの出力信号をAD変換して加速度データaを出力する。この加速度データaは、携帯機器1に固定された座標系における慣性力と重力との合力を、x軸、y軸及びz軸の3成分を有するベクトルとして示すデータである。したがって、携帯機器1が静止状態または等速直線運動状態にあれば、加速度データaは携帯機器1に固定された座標系において重力加速度の大きさと方向とを示すベクトルデータとなる。
【0024】
3次元角速度センサ90は、X軸角速度センサ91、Y軸角速度センサ92、及びZ軸角速度センサ93を備える。角速度センサI/F94は、各センサからの出力信号をAD変換して角速度データgを出力する。角速度データgは、各軸の回りの角速度を示す3次元のベクトルデータである。なお、角速度データgには、3次元角速度センサ90のオフセットgOFFが重畳する。
【0025】
CPU10は、ROM30に格納されている状態推定プログラム100を実行することによって、動的システムの状態を表す複数の物理量、例えば、携帯機器1の姿勢、3次元磁気センサ70のオフセット、地磁気の強さや伏角等の物理量を推定する。すなわち、携帯機器1は、CPU10が状態推定プログラム100を実行することにより、状態推定装置として機能する。
【0026】
状態推定プログラム100は、初期値生成モジュール110と、カルマンフィルタモジュール120とを備える。カルマンフィルタモジュール120は、カルマンフィルタKFの演算を実行する。
【0027】
[2. カルマンフィルタの観測対象及び推定対象]
一般的に、カルマンフィルタは、動的システムの状態を表す複数の物理量の経時的な変化を推定する状態遷移モデルと、動的システムを観測する複数のセンサが計測する値(観測値)を推定する観測モデルと、を有する。そして、カルマンフィルタは、状態遷移モデルを用いて、ある時刻における動的システムの状態を表す複数の物理量(状態変数)を要素とする状態ベクトルから、単位時間が経過した後の状態ベクトルを推定する。次に、カルマンフィルタは、推定された状態ベクトルに基づいて、動的システムの状態を測定する複数のセンサの出力値を要素とする観測値ベクトルの値を推定する。さらに、推定された観測値ベクトルと、実際のセンサの出力値を要素とする観測値ベクトルとの差分として算出される観測残差に基づいて、推定された状態ベクトルを、実際の値(真値)に近い値へと更新し、更新後の状態ベクトルを出力する。
カルマンフィルタは、以上のような演算を繰り返すことにより、状態ベクトルを構成する複数の状態変数の各々を、実際の物理量を正確に表した値(真値)へと近付ける。
【0028】
本実施形態において、カルマンフィルタKFは、携帯機器1の姿勢q、地磁気の強さr、地磁気の伏角θ、携帯機器1の角速度ω、3次元角速度センサ90のオフセットgOFFの推定値gO、及び3次元磁気センサ70のオフセットmOFFの推定値mOを状態変数として採用し、これらを推定の対象とする。
これらの状態変数を要素とする時刻T=kにおける状態ベクトルxkは、以下の式(1)で表される。なお、各状態変数の右下に付された添え字「k」は、当該状態変数が時刻T=kにおける値であることを表す。
【数1】

【0029】
本実施形態では、姿勢qを、クォータニオンを用いて表現する。クォータニオンとは、物体の姿勢(回転状態)を表す4次元数である。具体的には、地上に固定された座標系(例えば、地上の任意の一点を原点とし、互いに直交する3つの方向、例えば、水平東、水平北、及び鉛直上向きを、それぞれx軸、y軸、及びz軸とする座標系)を定め、当該地上に固定された座標系の各軸と、携帯機器1に固定された座標系の各軸とが一致する姿勢qを基準姿勢と定義し、基準姿勢をq=(0、0、0、1)と表現する。このとき、携帯機器1の任意の姿勢qは、基準姿勢に対して単位ベクトルρの方向を回転軸として角度ψだけ回転した姿勢として表現できる。回転後の姿勢qは、式(2)で与えられる。
【数2】

【0030】
本実施形態におけるカルマンフィルタの観測対象は、3次元磁気センサ70から出力される磁気データm、3次元加速度センサ80から出力される加速度データa、及び3次元角速度センサ90から出力される角速度データgである。観測値ベクトルは、これら磁気データm、加速度データa、及び角速度データgを要素とする。時刻T=kにおける観測値ベクトルykは式(3)で与えられる。
【数3】

【0031】
初期値生成モジュール110は、時刻T=0における状態変数を要素とする初期値INIを算出する。初期値INIは、姿勢qの初期値q0、地磁気の強さrの初期値r0、地磁気の伏角θの初期値θ0、角速度ωの初期値ω0、3次元角速度センサ90のオフセット推定値gOの初期値gO,0、及び3次元磁気センサ70のオフセット推定値mOの初期値mO,0を要素として含む。
初期値INIは、カルマンフィルタの演算によって状態変数がなるべく早く正確な値に収束するような値に適宜設定すればよいが、例えば、以下のような値に設定してもよい。
【0032】
地磁気の強さrの初期値r0、及び地磁気の伏角θの初期値θ0は、例えば、GPS部60から供給される位置情報に基づいて生成することができる。これは、地球上の位置が特定できれば、その位置における地磁気の強さ及び伏角を知ることができるからである。具体的には、ROM30には、位置情報と地磁気の強さ及び伏角とを対応づけて記憶したルックアップテーブルLUT1が格納される。初期値生成モジュール110は、ルックアップテーブルLUT1を参照して、位置情報に対応する地磁気の強さ及び伏角を、地磁気の強さrの初期値r0及び地磁気の伏角θの初期値θ0として設定する。
なお、携帯機器1が衛星からの電波の届かない場所(例えば、地下街)にある場合には、GPS部60から位置情報が得られない。そのような場合には、携帯機器1が使われ得る地域の典型的な値を採用すればよい。その値もルックアップテーブルLUT1に格納されている。初期値生成モジュール110は、位置情報の取得が不能な場合には、典型的な値をルックアップテーブルLUT1から読み出す。例えば、日本で販売された携帯機器1については、明石市の地磁気の強さ及び伏角に基づいて、地磁気の強さrの初期値r0、及び地磁気の伏角θの初期値θ0を算出する。
【0033】
角速度ωの初期値ω0は、例えば、携帯機器1が静止していることを仮定して、「0」に設定する。3次元角速度センサ90のオフセット推定値gOの初期値gO,0は、通常「0」近辺に調整されているため、「0」に設定する。姿勢qの初期値q0に関しては、例えば、携帯機器1が一定方向に向いて静止していることを仮定して、実際の初期姿勢とのずれを小さくするような値を設定する。
【0034】
3次元磁気センサ70のオフセット推定値mOの初期値mO,0は、例えば、時刻T=0の3次元磁気センサ70の観測値m0、姿勢qの初期値q0、携帯機器1を使用する地域の地磁気ベクトルmtypical、及び、式(5)に示す行列B(q)を用いて、以下に示す式(4)で与えられる値に設定する。ここで、行列B(q)は、携帯機器1が姿勢qである場合に、地上に固定された座標系において表現されたベクトルを、携帯機器1に固定された座標系において表現するための座標変換行列である。なお、ROM30には、位置情報と地磁気ベクトルmtypicalとを対応づけて記憶したルックアップテーブルLUT2が記憶されている。初期値生成モジュール110は、GPS部60で生成される位置情報に基づいてルックアップテーブルLUT2を参照して地磁気ベクトルmtypicalを取得し、式(4)を演算することによって、オフセット推定値mOの初期値mO,0を得る。
【数4】

【0035】
初期値生成モジュール110は、以上のようにして生成された姿勢qの初期値q0、地磁気の強さrの初期値r0、地磁気の伏角θの初期値θ0、角速度ωの初期値ω0、3次元角速度センサ90のオフセット推定値gOの初期値gO,0、及び3次元磁気センサ70のオフセット推定値mOの初期値mO,0を要素とするベクトルである初期値INIを生成し、これを出力する。
【0036】
[3. カルマンフィルタによる演算]
次に、本実施形態に係るカルマンフィルタKFによる演算の概要について説明する。
カルマンフィルタKFは、動的システムの状態の経時的な変化を表す状態遷移モデルを用いて、ある時刻(時刻T=k−1)のシステムの状態を示す状態ベクトルxk−1から単位時間が経過した後(時刻T=k)の状態ベクトルxkを推定し、この推定値を、推定された状態ベクトル(推定状態ベクトル)x−kとして出力する。そして、カルマンフィルタKFは、各種センサからの出力を要素とする観測値ベクトルykと状態ベクトルxkとの関係を表す観測モデルを用いて、状態遷移モデルにより推定された状態ベクトルx−kに基づいて観測値ベクトルykを推定し、この推定値を、推定された観測値ベクトル(推定観測値ベクトル)y−kとして出力する。なお、本実施形態のカルマンフィルタKFは、非線形カルマンフィルタであるシグマポイントカルマンフィルタにより構成される。シグマポイントカルマンフィルタとは、状態ベクトルxk−1の周囲に複数のシグマポイントχk−1を設定し、これらの複数のシグマポイントχk−1を状態遷移モデルに適用することで、単位時間経過後のシグマポイントχ−kを推定し、シグマポイントの推定値(推定シグマポイント)χ−kの平均を算出することにより、推定された状態ベクトルx−kを求める演算である。従って、推定された観測値ベクトルy−kは、厳密には、推定された状態ベクトルx−kの周辺に存在する複数のシグマポイントの推定値χ−kに基づいて算出される。
その後、カルマンフィルタKFは、推定された観測値ベクトルy−kと、実際の観測値を要素とする観測値ベクトルykとの差分を観測残差ekとして算出する。また、カルマンフィルタKFは、推定された状態ベクトルx−kと、推定された観測値ベクトルy−kと、に基づいてカルマンゲインKkを算出する。そして、カルマンフィルタKFは、観測残差ekとカルマンゲインKkとを用いて推定された状態ベクトルx−kを更新し、更新後の状態ベクトル(状態ベクトルを更新したベクトル)x+kを算出する。
以上のような状態ベクトルxkの更新を繰り返すカルマンフィルタKFの演算により、状態ベクトルxkを実際の物理量を正確に表した値(真値)に近い正確な値へと近付けることができる。
【0037】
[3.1. カルマンフィルタ演算部の動作の概要]
本実施形態におけるカルマンフィルタKFの状態遷移モデルは以下に示す式(6)で与えられ、観測モデルは以下に示す式(7)で与えられる。本実施形態では、式(6)に現れる関数f及び式(7)に現れる関数hは、非線形の関数である。
【数5】

【0038】
ここで、状態ベクトルxkはn次元のベクトルであり、観測値ベクトルykはm次元のベクトルである。なお、本実施形態では、n=15であり、m=9である。また、式(6)に現れるプロセスノイズuk及び式(7)に現れる観測ノイズvkは0を中心とするガウスノイズである。
式(6)は、時刻T=kにおける状態ベクトルxkが、時刻T=k−1における状態ベクトルxk−1を関数fに代入して得られた値と、時刻T=k−1におけるプロセスノイズuk−1とを加算することにより推定されるものであることを示している。
また、式(7)は、時刻T=kにおける観測値ベクトルykが、時刻T=kにおける状態ベクトルxkを関数hに代入して得られる値と、時刻T=kにおける観測ノイズvkとを加算することにより推定されることを示している。
なお、プロセスノイズukの共分散をQ、観測ノイズvkの共分散をRと表す。
【0039】
時刻T=kにおける観測残差ekは、実際の観測値ベクトルykと、推定された観測値ベクトルy−kとに基づいて定められるベクトルであり、以下に示す式(8)で表される。カルマンフィルタKFは、観測残差ekと、式(9)に示すカルマンゲインKkとを用いて、以下の式(10)に示すように、推定された状態ベクトルx−kを更新し、更新後の状態ベクトルx+kを算出する。また、カルマンフィルタKFは、以下の式(11)に示すように、状態ベクトルxkの推定誤差の共分散Pkを更新する。
なお、P−kは、推定された状態ベクトルx−kの推定誤差の共分散であり、P+kは、更新後の状態ベクトルx+kの推定誤差の共分散である。
また、Pyykは、観測残差ekの共分散であり、Pxykは、推定された状態ベクトルx−kと、推定された観測値ベクトルy−kとの相互共分散行列である。
【数6】

【0040】
観測モデルを用いて推定された観測値ベクトルy−kは、式(7)に示すように、観測モデルを用いて推定された状態ベクトルx−kに基づいて算出される理論値である。よって、観測モデルを用いて推定された観測値ベクトルy−kと実際のセンサ出力に基づく観測値ベクトルykとの差分である観測残差ekは、推定された状態ベクトルx−kと実際の物理量を正確に表した値(真値)との近似度を示す値である。
カルマンフィルタKFは、式(10)に示すように、観測残差ekを用いて、推定された状態ベクトルx−kを、真値に近い更新後の状態ベクトルx+kへと更新する。
【0041】
[3.2. シグマポイントカルマンフィルタによる演算]
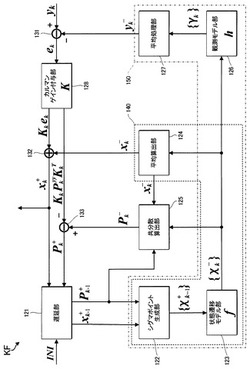
本実施形態において、カルマンフィルタKFは、アンセンテッド変換を用いたシグマポイントカルマンフィルタにより構成される。以下では、図3に示すカルマンフィルタKFの機能ブロック図を参照しつつ、カルマンフィルタKFによる演算の詳細を説明する。
【0042】
遅延部121は、加算器132から出力される更新後の状態ベクトルx+kを、単位時間(時刻T=k−1から時刻T=kに相当する時間)だけ遅延させることで、状態ベクトルx+k−1を生成し、これを、シグマポイント生成部122に対して出力する。なお、初回の演算(時刻T=0)では、遅延部121は、初期値生成モジュール110が出力する初期値INIを用いて、状態ベクトルx+k−1を生成する。
また、遅延部121は、減算器133から出力される更新後の状態ベクトルx+kの推定誤差の共分散P+kを単位時間遅延させることで、状態ベクトルx+k−1の推定誤差の共分散P+k−1を生成し、これを、シグマポイント生成部122及び共分散算出部125に対して出力する。
【0043】
シグマポイント生成部122は、状態ベクトルx+k−1に基づいて、a個のシグマポイントχ+k−1(i)(i=1,2,…a)を生成する(aは、2以上の自然数)。シグマポイントχ+k−1(i)の生成は、以下に示す公知の方法を適用する。
シグマポイント生成部122は、まず、状態ベクトルx+k−1の推定誤差の共分散P+k−1から、式(12)に示す共分散P+k−1の平方根を表すn行n列の行列を生成する。次に、シグマポイント生成部122は、共分散P+k−1の平方根を表す行列と、各種係数とに基づいて、a個のシグマポイント算出用ベクトルを定める。シグマポイント算出用ベクトルは、n次元のベクトルである。その後、シグマポイント生成部122は、状態ベクトルx+k−1と、a個のシグマポイント算出用ベクトルとに基づいて、a個のシグマポイントχ+k−1(i)を生成し、これを状態遷移モデル部123に対して出力する。
なお、a個のシグマポイントχ+k−1(i)の生成において用いられる各種係数は、後述する式(14)における重みwiの生成にも用いられる値であり、公知の方法により定められる。また、a個のシグマポイント算出用ベクトルには0ベクトルが含まれていても構わない。
【数7】

【0044】
状態遷移モデル部123は、式(13)に示すように、時刻T=k−1におけるa個のシグマポイントχ+k−1(i)の各々を、状態遷移モデルに適用することにより、時刻T=kにおけるa個のシグマポイントの推定値χ−k(i)を算出する。
【数8】

【0045】
次に、平均算出部124は、式(14)に示すように、時刻T=kにおけるa個のシグマポイントの推定値χ−k(i)の重み付き平均を計算することで、推定された状態ベクトルx−kを算出し、これを出力する。なお、式(14)に現れる重みwiは、シグマポイントχ+k−1(i)の生成において用いられた各種係数に基づいて定められる。
このように、シグマポイント生成部122、状態遷移モデル部123、及び平均算出部124は、状態ベクトルx+k−1から、推定された状態ベクトルx−kを算出する推定状態ベクトル算出部140として機能する。
【数9】

【0046】
共分散算出部125は、推定された状態ベクトルx−kの推定誤差の共分散P−kを算出する。推定された状態ベクトルx−kの推定誤差の共分散P−kは、式(15)に示すように、a個のシグマポイントの推定値χ−k(i)、推定された状態ベクトルx−k、重みwi、及びプロセスノイズuk−1の共分散Qに基づいて算出することができる。
但し、本実施形態では、処理負荷を削減する観点から、共分散P−kのうち一部の成分は、式(15)を用いずに、後述する式(30)に基づいて算出する。この点についての詳細は後述する。
【数10】

【0047】
一方、観測モデル部126は、式(16)に示すように、時刻T=kにおけるa個のシグマポイントの推定値χ−k(i)の各々を、観測モデルに適用することにより、a個の推定観測値γk(i)を算出する。
【数11】

【0048】
そして、平均処理部127は、式(17)に示すように、a個の推定観測値γk(i)の平均を演算することにより、推定された観測値ベクトルy−kを算出する。
このように、シグマポイント生成部122、状態遷移モデル部123、観測モデル部126、及び平均処理部127は、状態ベクトルx+k−1から、推定された観測値ベクトルy−kを算出する推定観測値ベクトル算出部150として機能する。
【数12】

【0049】
次に、平均処理部127は、式(18)に示す観測残差の共分散Pyykを算出する。
【数13】

【0050】
減算器(観測残差生成部)131は、式(8)に示したように、観測値ベクトルykと、推定された観測値ベクトルy−kとの差分として、観測残差ekを算出する。
カルマンゲイン付与部128は、式(19)に示す相互共分散行列Pxykを算出する。次に、カルマンゲイン付与部128は、式(9)に示したように、観測残差の共分散Pyykと、相互共分散行列Pxykとに基づいて、カルマンゲインKkを算出する。その後、カルマンゲイン付与部128は、式(10)の右辺第2項(Kkek)を演算し、その結果を加算器132に対して出力する。
また、カルマンゲイン付与部128は、観測残差の共分散PyykとカルマンゲインKkとに基づいて、式(11)の右辺第2項(KkPyykKTk)を演算し、その結果を減算器133に対して出力する。
【数14】

【0051】
加算器(更新部)132は、式(10)に示したように、推定された状態ベクトルx−kと、カルマンゲイン付与部128から出力される式(10)の右辺第2項(Kkek)と、を加算することにより、更新後の状態ベクトルx+kを算出する。
減算器133は、式(11)に示したように、推定された状態ベクトルx−kの推定誤差の共分散P−kと、カルマンゲイン付与部128から出力される式(11)の右辺第2項(KkPyykKTk)との差分として、更新後の状態ベクトルx+kの推定誤差の共分散P+kを算出する。
【0052】
[3.3. 状態遷移モデル]
次に、状態遷移モデル部123の演算で用いる状態遷移モデルについて説明する。
【0053】
本実施形態に係る状態遷移モデルにおいて、状態ベクトルxkを構成する状態変数のうち、姿勢qについての状態遷移は、式(21)に示す関数fq(q,ω)を用いて、式(20)により定義される。式(20)は、時刻T=kにおける推定された状態ベクトルx−kを構成する状態変数である姿勢q−kが、時刻T=k−1における状態ベクトルx+k−1を構成する状態変数である姿勢q+k−1及び角速度ω+k−1に基づいて推定されることを示している。
式(21)に示す関数fq(q,ω)は、式(6)に示した関数fのうち、姿勢qを算出する部分のみを表した関数である。式(21)の右辺の演算子Ωは、式(22)により定義される。ここで、I3×3は3行3列の単位行列を表し、3次元ベクトルl=(l1,l2,l3)に対して、[l×]という記号を式(23)で定義する。また、測定時間間隔(時刻T=k−1から時刻T=kまでの間隔)をΔtで表したとき、演算子Ωを構成する成分Ψを、式(24)で定義する。
【数15】

【0054】
姿勢qは、クォータニオンで表現されるため、正規化条件||q||=1が満たされる必要がある。しかし、シグマポイントカルマンフィルタを用いて状態ベクトルxkを更新する場合、更新後の状態ベクトルx+kは、式(14)に示すように、シグマポイントの推定値χ−k(i)に重みwiを付与した重み付き平均として算出されるため、(更新前の)状態ベクトルxk−1のノルムと、更新後の状態ベクトルx+kのノルムとは、異なる値となることがある。従って、シグマポイントカルマンフィルタの演算を行う場合、(更新前の)状態ベクトルxk−1の要素である姿勢qk−1のノルムと、更新後の状態ベクトルx+kの要素である姿勢qkのノルムとは、異なる値となる可能性が存在する。つまり、シグマポイントカルマンフィルタの演算を行う場合、姿勢qについての正規化条件が満たされなくなる可能性が存在する。
そこで、姿勢qに対して何らかの演算が行われるときには、演算後の結果をそのベクトル自身の大きさで正規化する。なお、より厳密に正規化条件を保つためには、状態ベクトルxkを構成する要素のうち姿勢qkについてはMRPs (modified Rodrigues parameters)を用いて前時刻との差分情報だけに限定し、カルマンフィルタの外部にある姿勢情報をカルマンフィルタから得られる差分情報に基づいて更新すればよい。
【0055】
地磁気の強さr及び地磁気の伏角θは、変化を予測することが難しい。そこで、本実施形態に係る状態遷移モデルでは、便宜上、時刻T=kにおける地磁気の強さrk及び伏角θkと、時刻T=k−1における地磁気の強さrk−1及び伏角θk−1とは等しい値であるという前提を置く。
同様に、3次元角速度センサ90のオフセット推定値gOも、変化を予測することが難しい。そこで、本実施形態に係る状態遷移モデルでは、便宜上、時刻T=kにおけるオフセット推定値gO,Kと、時刻T=k−1におけるオフセット推定値gO,K−1とは等しい値であるという前提を置く。
【0056】
携帯機器1の角速度ωは、携帯機器1の利用者による携帯機器1の動かし方に依存して変化するため、時刻T=k−1の角速度ωk−1を用いて、時刻T=kにおける角速度ωkを定式化することは難しい。そこで、本実施形態に係る状態遷移モデルでは、便宜上、時刻T=kにおける角速度ωkと、時刻T=k−1における角速度ωk−1とは等しいと仮定する。
【0057】
前述のとおり、3次元磁気センサ70のオフセットmOFFは、携帯機器1の部品が発する内部磁界である。従って、携帯機器1の内部状態が一定である間は、オフセットmOFFも変化しない。一方、携帯機器1の内部状態が変化した場合、例えば、携帯機器1に搭載された部品を流れる電流の大きさが変化した場合や、携帯機器1に搭載された部品の着磁状況が変化した場合には、オフセットmOFFも変化する。すなわち、携帯機器1の内部状態は、携帯機器1の利用者による携帯機器1の操作や、携帯機器1の外部の環境等に依存して変化する。従って、オフセットmOFFが変化するタイミングやオフセットmOFFの変化量を予測することは困難であり、時刻T=k−1におけるオフセット推定値mO,K−1を用いて、時刻T=kにおけるオフセット推定値mO,kを定式化することは難しい。
そこで、本実施形態に係る状態遷移モデルでは、便宜上、時刻T=kにおけるオフセット推定値mO,kと、時刻T=k−1におけるオフセット推定値mO,k−1とは等しいと仮定する。
【0058】
このように、本実施形態に係る状態遷移モデルでは、以下に示す式(25)のように、状態ベクトルxkを構成する状態変数のうち、姿勢q以外は、前の時刻から変化しないという前提を置く。
【数16】

【0059】
ここで、式(1)に示した状態ベクトルxkを、式(26)のように、姿勢qkと、姿勢qk以外の要素を表すベクトルβkとに分離して表現した場合、ベクトルβkについて、式(27)が成立する。すなわち、状態ベクトルx+k−1のうち、姿勢(第2ベクトル)q+k−1以外の要素を表すベクトル(第1ベクトル)β+k−1と、推定された状態ベクトルx−kのうち、姿勢(推定第2ベクトル)q−k以外の要素を表すベクトル(推定第1ベクトル)β−kとは等しい。
【数17】

【0060】
式(27)が成立する場合、式(13)から明らかなように、シグマポイントχ+k−1(i)のうちベクトルβ+k−1に相当する要素と、シグマポイントの推定値χ−k(i)のうちベクトルβ−kに相当する要素とは、等しくなる。
従って、式(27)が成立する場合、状態ベクトルx+k−1の推定誤差の共分散P+k−1のうち、ベクトルβ+k−1の推定誤差の共分散を表す成分と、推定された状態ベクトルx−kの推定誤差の共分散P−kのうち、ベクトルβ−kの推定誤差の共分散を表す成分とは、プロセスノイズuk−1の共分散Qを考慮しなければ、等しいものと看做すことができる(段落[0046]参照)。
【0061】
ここで、共分散Pkを、式(28)に示すように、行列Pqq,k、行列Pqβ,k、行列Pqβ,kT、及び行列Pββ,kの、4つの行列に分割する。行列Pqq,kは、姿勢qkに基づいて定められる、4行4列の行列である。行列Pqβ,kは、姿勢qkとベクトルβkとに基づいて定められる、4行11列の行列である。行列Pββ,kは、ベクトルβkに基づいて定められる、11行11列の行列である。具体的には、行列Pββ,kは、ベクトルβkの推定誤差の共分散を表す行列である。
【数18】

【0062】
また、プロセスノイズukの共分散Qを、式(29)のように、4行4列の行列Qqq、4行11列の行列Qqβ、及び11行11列の行列Qββを用いて表す。
式(6)に示したとおり、プロセスノイズukは、状態ベクトルxkを状態遷移モデルに適用する際に生じるプロセスノイズであり、式(29)に示す共分散Qは、当該プロセスノイズukの共分散を表す。従って、式(29)に現れる、行列Qββは、状態ベクトルxkを状態遷移モデルに適用する際に生じるプロセスノイズのうち、状態ベクトルxkの中で姿勢qk以外の要素を表すベクトルβkに生じるプロセスノイズの共分散を表す。
このとき、行列P−ββ,kは、式(30)に示すように、行列P+ββ,k−1と、行列Qββとの和として定められる。
【数19】

【0063】
共分散P−kの全ての成分を式(15)に基づいて求める場合、n行1列のベクトルと1行n列のベクトルとを乗算してn行n列の行列を求める演算を、a回繰り返すことが必要になる。
一方、式(30)を用いる場合、行列P−ββ,kは、1ステップ前に(時刻T=k−1において)既に算出されている行列P+ββ,k−1と、行列Qββとを単純に加算することにより算出される。そして、共分散P−kは、行列P−ββ,k以外の成分、すなわち、4行4列の行列P−qq,k及び4行11列の行列P−qβ,kのみを、式(15)による演算により求めればよい。この結果、15行15列の共分散P−kの全ての成分を、式(15)を用いて算出する場合に比べて、共分散算出部125における計算量を大幅に低減することが可能となる。
【0064】
なお、状態遷移モデルにおいて、式(25)及び式(27)に示すように、姿勢q以外は、前の時刻から変化しないという前提を置いた場合であっても、状態ベクトルxkは、カルマンフィルタの演算において観測残差ekに基づいて更新される。従って、姿勢qk以外の要素を表すベクトルβkも、カルマンフィルタの演算を繰り返す中で、観測残差ekに基づいて真値に近づくように更新される。
【0065】
[3.4. 観測モデル]
次に、観測モデル部126で行われる演算において用いられる観測モデルについて説明する。
【0066】
3次元角速度センサ90から出力される角速度データgの推定値γgyroは、角速度ωと、3次元角速度センサ90のオフセット推定値gOとを用いて、式(31)で与えられる。
【数20】

【0067】
また、地上に固定された座標系において、地磁気を表すベクトルは、式(32)で与えられる。従って、3次元磁気センサ70から出力される磁気データmの推定値γmagは、3次元磁気センサ70のオフセット推定値mOと、式(5)で示した行列B(q)とを用いて、式(33)で与えられる。
【数21】

【0068】
また、地上に固定された座標系において、重力を表すベクトルを重力加速度で正規化したベクトルは、式(34)で与えられる。従って、3次元加速度センサ80から出力される加速度データaの推定値γaccは、式(5)で示した行列B(q)を用いて、式(35)で与えられる。
【数22】

【0069】
従って、式(3)を式(8)の右辺第1項に代入し、式(31)、式(33)、及び式(35)を用いて式(8)の右辺第2項を表すことにより、式(8)を、以下の式(36)に変形することができる。このとき、観測残差ekは、式(36)により算出される。
【数23】

【0070】
[4. 結論]
以上に示したように、本実施形態に係る状態推定装置は、シグマポイントカルマンフィルタの演算において用いられる状態ベクトルxkを、姿勢qkと、ベクトルβkとに分離して表現し、状態ベクトルx+k−1を構成する要素の一部であるベクトルβ+k−1と、推定された状態ベクトルx−kを構成する要素の一部であるベクトルβ−kとが等しいという前提を置いた。
そして、本実施形態に係る状態推定装置は、推定された状態ベクトルx−kの推定誤差の共分散P−kのうちベクトルβ−kの推定誤差の共分散を表す成分を、状態ベクトルx+k−1の推定誤差の共分散P+k−1のうちベクトルβ+k−1の推定誤差の共分散を表す成分と、プロセスノイズuk−1の共分散Qのうちベクトルβ+k−1に生じるプロセスノイズの共分散を表す成分とを単純に加算することで算出した。
これにより、共分散P−kの全ての成分を式(15)に基づいて求める場合と比較して、シグマポイントカルマンフィルタの計算負荷を大幅に低減することが可能となり、状態推定装置の処理速度の向上、及び携帯機器1の低消費電力化が可能となった。
【0071】
<B.変形例>
本発明は上述した実施形態に限定されるものではなく、例えば、以下の変形が可能である。また、以下に示す変形例のうちの2以上の変形例を組み合わせることもできる。
【0072】
(1)変形例1
上述した実施形態では、状態ベクトルxを構成する要素して、携帯機器1の姿勢q、地磁気の強さr、地磁気の伏角θ、携帯機器1の角速度ω、3次元角速度センサ90のオフセット推定値gO、及び3次元磁気センサ70のオフセット推定値mOを採用し、これら6個の状態変数をカルマンフィルタの演算における推定の対象としたが、本発明はこれに限定されるものでは無い。例えば、状態ベクトルxを、これら6個の状態変数のうちの一部の状態変数により構成し、当該一部の状態変数をカルマンフィルタの演算における推定の対象とするものであってもよい。
【0073】
(2)変形例2
上述した実施形態では、観測値ベクトルyを、3次元磁気センサ70から出力される磁気データm、3次元加速度センサ80から出力される加速度データa、及び3次元角速度センサ90から出力される角速度データgを要素とするベクトルとしたが、本発明はこれに限定されるものでは無く、磁気データm、加速度データa、及び角速度データgのうちの一部のみを利用して観測値ベクトルyを生成してもよい。
【0074】
(3)変形例3
上述した実施形態では、平均算出部124は、式(14)に示すように、推定された状態ベクトルx−kを、a個のシグマポイントの推定値χ−k(i)の重み付き平均として算出したが、本発明はこれに限定されるものではない。
例えば、平均算出部124は、推定された状態ベクトルx−kを構成する要素の一部であるベクトルβ−kを、式(14)を用いず、単純に、状態ベクトルx+k−1を構成する要素の一部であるベクトルβ+k−1と等しい値に設定してもよい。この場合、平均算出部124は、推定された状態ベクトルx−kのうち、姿勢q−kについてのみ、式(14)の重み付き平均を算出する演算により算出する。これにより、15次元のベクトルである推定された状態ベクトルx−kのうち、11次元のベクトルβ−kについては、単純な値の代入により算出することが可能となるため、推定された状態ベクトルx−kの算出に係る処理負荷を、大幅に低減することができる。
【符号の説明】
【0075】
1…携帯機器、KF…カルマンフィルタ、121…遅延部、122…シグマポイント生成部、123…状態遷移モデル部、124…平均算出部、125…共分散算出部、126…観測モデル部、127…平均処理部、127…推定観測値ベクトル算出部、128…カルマンゲイン付与部、131…減算器、132…加算器、133…減算器、140…推定状態ベクトル算出部、150…推定観測値ベクトル算出部、K…カルマンゲイン、xk…状態ベクトル、x−k…推定された状態ベクトル、qk…姿勢、βk…ベクトル、Pk…状態ベクトルの推定誤差の共分散、Q…プロセスノイズの共分散、ek…観測残差、yk…観測値ベクトル、y−k…推定された観測値ベクトル。
【技術分野】
【0001】
本発明は、カルマンフィルタ、状態推定装置、カルマンフィルタの制御方法、及びカルマンフィルタの制御プログラムに関する。
【背景技術】
【0002】
近年、携帯機器の高性能化及び多用途化に伴い、地磁気の方向や携帯機器の姿勢等の推定機能を備える携帯機器の研究開発が盛んに行われている。地磁気の方向や携帯機器の姿勢等を推定する場合、地磁気センサ等の単体のセンサからの出力のみを利用して推定するよりも、異種の物理量を測定する複数のセンサからの出力を統合して推定する方が、より高速に正確な値を推定することができる。
【0003】
異種の物理量を測定する複数のセンサの出力を統合し、動的システムの状態を推定する方法として、拡張カルマンフィルタ(EKF)やシグマポイントカルマンフィルタ(SPKF)等の非線形カルマンフィルタを用いる方法が知られている。
例えば、特許文献1には、3軸の角速度センサ及び3軸の加速度センサと非線形カルマンフィルタとを実装した姿勢角計測装置が開示されている。また、非特許文献1には、3軸角速度センサ、3軸加速度センサ、及び3軸地磁気センサからの出力信号を、アンセンテッド変換を用いたシグマポイントカルマンフィルタによって統合し、姿勢を推定する方法が開示されている。シグマポイントカルマンフィルタは、他のカルマンフィルタに比べて、非線形システムのモデル化に適した演算方法であり、シグマポイントカルマンフィルタを用いることで、非線形な動的システムの状態を正確に推定することができる。
【先行技術文献】
【特許文献】
【0004】
【特許文献1】特開平9−5104号公報
【非特許文献】
【0005】
【非特許文献1】Wolfgang Gunthner, “Enhancing Cognitive Assistance Systems with Inertial Measurement Units”, Springer, 2008
【発明の概要】
【発明が解決しようとする課題】
【0006】
しかし、シグマポイントカルマンフィルタによる演算は計算量が多いため、シグマポイントカルマンフィルタが実装される機器には、大容量のメモリと高性能のCPUとを備えることが必要となる。そして、シグマポイントカルマンフィルタによる演算を行う場合、多くの電力が消費される。特に、シグマポイントカルマンフィルタを実装した機器が、バッテリーで給電される携帯機器の場合、機器の長時間使用が困難になるという課題が存在した。
本発明は、上述した点に鑑みてなされたものであり、シグマポイントカルマンフィルタの演算を簡素化し、高速且つ低消費電力な状態推定装置の実現を解決課題とする。
【課題を解決するための手段】
【0007】
以下、本発明について説明する。なお、本発明の理解を容易にするために本実施形態、変形例、及び添付図面の参照符号を括弧書きにて付記するが、それにより本発明が本実施形態に限定されるものではない。
【0008】
上記課題を解決するため、本発明に係るカルマンフィルタは、第1ベクトル(β+k−1)及び第2ベクトル(q+k−1)を要素とする状態ベクトル(x+k−1)と、前記状態ベクトルの推定誤差の共分散(P+k−1)と、に基づいて、状態遷移モデル(f)を用いて、推定第1ベクトル(β−k)及び推定第2ベクトル(q−k)を要素とする推定状態ベクトル(x−k)を算出する推定状態ベクトル算出部と、前記推定状態ベクトルの推定誤差の共分散(P−k)を算出する共分散算出部と、前記状態遷移モデル及び観測モデル(h)を用いて、前記状態ベクトルから、推定観測値ベクトル(y−k)を算出する推定観測値ベクトル算出部と、前記推定観測値ベクトルと、外部の複数のセンサから出力される観測値を要素とする観測値ベクトル(yk)とに基づいて、観測残差(ek)を算出する観測残差生成部と、前記観測残差と、前記推定状態ベクトルとに基づいて、前記状態ベクトルを更新したベクトルを算出する更新部と、を備え、前記推定状態ベクトル算出部は、前記推定第1ベクトルを、前記第1ベクトルと等しい値に設定し、前記共分散算出部は、前記状態ベクトルの推定誤差の共分散のうち、前記第1ベクトルの推定誤差の共分散を表す成分(P+ββ,k−1)、及び前記状態遷移モデルにおいて前記状態ベクトルに生じるプロセスノイズの共分散のうち、前記第1ベクトルに生じるプロセスノイズの共分散を表す成分(Qββ)を加算して、前記推定状態ベクトルの推定誤差の共分散のうち、前記推定第1ベクトルの推定誤差の共分散を表す成分(P−ββ,k)を算出する、ことを特徴とする。
【0009】
この発明によれば、共分散算出部は、推定状態ベクトルの推定誤差の共分散のうち推定第1ベクトルの推定誤差の共分散を表す成分を、2個の行列を加算することで算出する。
一般的に、あるベクトルの推定誤差の共分散は、まず、当該あるベクトルの推定誤差を表すベクトルを算出し、その後、推定誤差を表すベクトルと、推定誤差を表すベクトルを転置したベクトルとの積を算出することにより求められる。よって、あるベクトルの推定誤差の共分散を求めるためには、推定誤差を表すベクトルを算出する演算の他に、当該あるベクトルの次元を表す数の二乗に相当する回数の演算が必要になる。
シグマポイントカルマンフィルタは、複数のシグマポイントに基づいて、推定状態ベクトルの推定誤差を表すベクトルを複数生成し、生成した複数の推定誤差を表すベクトルを用いて、推定状態ベクトルの推定誤差の共分散を算出する。従って、推定状態ベクトルの推定誤差の共分散を求めるためには、推定状態ベクトルの次元を表す数の二乗に相当する回数の演算を、更に、シグマポイントの個数に相当する回数だけ繰り返すことが必要となる。このように、推定状態ベクトルの推定誤差の共分散を求める演算は、計算量が多く、シグマポイントカルマンフィルタの処理負荷を増大させる要因となっていた。
これに対して、この発明の共分散算出部は、推定状態ベクトルの推定誤差の共分散のうちの一部の成分を、2つの行列の加算という単純な演算により算出するため、従来の方法に従って計算した場合に比べて、推定状態ベクトルの推定誤差の共分散を求める演算に係る計算量の大幅な低減を可能とした。これにより、シグマポイントカルマンフィルタの演算の高速化と、シグマポイントカルマンフィルタの演算に必要な電力の低減が可能となった。
なお、この発明の推定状態ベクトル算出部は、推定第1ベクトルを第1ベクトルと等しい値に設定する。しかし、第1ベクトルは、カルマンフィルタの演算において、値を全く変化させない訳ではない。すなわち、推定第1ベクトルを要素として含む推定状態ベクトルは、更新部において観測残差による更新がなされ、カルマンフィルタの推定対象であるシステムの状態を正確に表す値(真値)へと更新される。これにより、この発明に係るカルマンフィルタは、システムの状態を正確に推定することができる。
【0010】
また、上述したカルマンフィルタにおいて、前記推定状態ベクトル算出部は、前記状態ベクトルと、前記状態ベクトルの推定誤差の共分散とに基づいて、複数のシグマポイント(χ+k−1)を生成するシグマポイント生成部と、前記状態遷移モデルを用いて、前記複数のシグマポイントから、複数の推定シグマポイント(χ−k)を算出する状態遷移モデル部と、前記推定状態ベクトル(x−k)を算出する平均算出部と、を備え、前記状態遷移モデル部は、前記推定シグマポイントのうち、前記推定第2ベクトル(q−k)を算出するために用いられる要素以外の要素を、前記シグマポイントのうち、前記第1ベクトル(β+k−1)に基づいて生成された要素と等しい値に設定し、前記平均算出部は、前記推定第1ベクトル(β−k)を、前記第1ベクトル(β+k−1)と等しい値に設定し、前記推定第2ベクトル(q−k)を、前記複数の推定シグマポイント(χ−k)に基づいて算出することが好ましい。
【0011】
この発明によれば、状態ベクトルの推定値を、複数のシグマポイントを用いて算出する。これにより、状態遷移モデルを用いた状態ベクトルの推定において、状態ベクトルが有する誤差による影響と、カルマンフィルタが推定対象とするシステムの非線形性による影響とを低減させることができ、状態遷移モデルにおける推定精度の低下を防止することができる。すなわち、この発明によれば、カルマンフィルタが、システムの状態を正確に推定することが可能となる。
また、この発明によれば、推定第1ベクトルを、第1ベクトルと等しい値に設定し、推定第2ベクトルのみを、複数の推定シグマポイントに基づいて算出するため、推定状態ベクトルの算出に係る計算負荷を低減させることが可能となる。
【0012】
次に、本発明に係る状態推定装置は、システムを観測して観測値を各々出力する複数のセンサと、上記のうちいずれかのカルマンフィルタとを備えることを特徴とする。
この発明によれば、高速なカルマンフィルタの演算が可能で、且つ低消費電力な状態推定装置が実現される。
【0013】
次に、本発明に係るカルマンフィルタの制御方法は、システムの状態を推定するカルマンフィルタの制御方法であって、第1ベクトル及び第2ベクトルを要素とする状態ベクトルと、前記状態ベクトルの推定誤差の共分散と、に基づいて、状態遷移モデルを用いて、推定第1ベクトル及び推定第2ベクトルを要素とする推定状態ベクトルを算出する工程と、前記推定状態ベクトルの推定誤差の共分散を算出する工程と、前記状態遷移モデル及び観測モデルを用いて、前記状態ベクトルから、推定観測値ベクトルを算出する工程と、前記推定観測値ベクトルと、外部の複数のセンサから出力される観測値を要素とする観測値ベクトルとに基づいて、観測残差を算出する工程と、前記観測残差と、前記推定状態ベクトルとに基づいて、前記状態ベクトルを更新したベクトルを算出する工程と、を備え、前記推定状態ベクトルを算出する工程は、前記推定第1ベクトルを、前記第1ベクトルと等しい値に設定し、前記推定状態ベクトルの推定誤差の共分散を算出する工程は、前記状態ベクトルの推定誤差の共分散のうち、前記第1ベクトルの推定誤差の共分散を表す成分、及び前記状態遷移モデルにおいて前記状態ベクトルに生じるプロセスノイズの共分散のうち、前記第1ベクトルに生じるプロセスノイズの共分散を表す成分を加算して、前記推定状態ベクトルの推定誤差の共分散のうち、前記推定第1ベクトルの推定誤差の共分散を表す成分を算出する、ことを特徴とする。
【0014】
この発明によれば、推定状態ベクトルの推定誤差の共分散を求める演算の計算量を、従来の方法に従って計算した場合に比べて大幅に低減することが可能となり、カルマンフィルタの演算の高速化と、カルマンフィルタの演算に必要な電力の低減が可能となった。
【0015】
次に、本発明に係るカルマンフィルタの制御プログラムは、システムの状態を推定するカルマンフィルタの制御プログラムであって、第1ベクトル及び第2ベクトルを要素とする状態ベクトルと、前記状態ベクトルの推定誤差の共分散と、に基づいて、状態遷移モデルを用いて、推定第1ベクトル及び推定第2ベクトルを要素とする推定状態ベクトルを算出する処理と、前記推定状態ベクトルの推定誤差の共分散を算出する処理と、前記状態遷移モデル及び観測モデルを用いて、前記状態ベクトルから、推定観測値ベクトルを算出する処理と、前記推定観測値ベクトルと、外部の複数のセンサから出力される観測値を要素とする観測値ベクトルとに基づいて、観測残差を算出する処理と、前記観測残差と、前記推定状態ベクトルとに基づいて、前記状態ベクトルを更新したベクトルを算出する処理と、をコンピュータに実行させ、前記推定状態ベクトルを算出する処理は、前記推定第1ベクトルを、前記第1ベクトルと等しい値に設定し、前記推定状態ベクトルの推定誤差の共分散を算出する処理は、前記状態ベクトルの推定誤差の共分散のうち、前記第1ベクトルの推定誤差の共分散を表す成分、及び前記状態遷移モデルにおいて前記状態ベクトルに生じるプロセスノイズの共分散のうち、前記第1ベクトルに生じるプロセスノイズの共分散を表す成分を加算して、前記推定状態ベクトルの推定誤差の共分散のうち、前記推定第1ベクトルの推定誤差の共分散を表す成分を算出する、ことを特徴とする。
【0016】
この発明によれば、推定状態ベクトルの推定誤差の共分散を求める演算の計算量を、従来の方法に従って計算した場合に比べて大幅に低減することが可能となり、カルマンフィルタの演算の高速化と、カルマンフィルタの演算に必要な電力の低減が可能となった。
【図面の簡単な説明】
【0017】
【図1】本発明の実施形態に係る携帯機器の構成を示すブロック図である。
【図2】携帯機器の外観を示す斜視図である。
【図3】本発明の実施形態に係るカルマンフィルタの機能ブロック図である。
【発明を実施するための形態】
【0018】
<A.実施形態>
本発明の実施の形態について図面を参照して説明する。
【0019】
[1. 機器構成及びソフトウェア構成]
図1は、本発明の実施形態に係る携帯機器のブロック図であり、図2は携帯機器の外観を示す斜視図である。携帯機器1は、携帯機器1の姿勢を変えることにより変化する画面の向く方向に応じて地図などの画像を回転させることによって、画像によって表される方位を、現実空間の方位に追従させる機能を備える。この機能は、各種センサの出力に基づいてカルマンフィルタの演算を行い、携帯機器1の姿勢等を推定することによって実現される。
【0020】
携帯機器1は、各種の構成要素とバスを介して接続され装置全体を制御するCPU10、CPU10の作業領域として機能するRAM20、各種のプログラムやデータを記憶したROM30、通信を実行する通信部40、画像を表示する表示部50、及びGPS部60を備える。GPS部60は、GPS衛星からの信号を受信して携帯機器1の位置情報(緯度、経度)を生成するものである。また、携帯機器1は、地磁気を検出して磁気データを出力する3次元磁気センサ70、加速度を検出して加速度データを出力する3次元加速度センサ80、及び角速度を検出して角速度データを出力する3次元角速度センサ90を備える。
【0021】
3次元磁気センサ70は、X軸磁気センサ71、Y軸磁気センサ72、及びZ軸磁気センサ73を備える。各センサは、MI素子(磁気インピーダンス素子)、MR素子(磁気抵抗効果素子)などを用いて構成することができる。磁気センサI/F74は、各センサからの出力信号をAD変換して磁気データmを出力する。この磁気データmは、x軸、y軸およびz軸の3成分によって表されるベクトルデータである。
【0022】
ところで、3次元磁気センサ70が搭載される携帯機器1は、着磁性を有する各種金属や、電気回路等、磁界を発生させる部品が備えられることが多い。このため、3次元磁気センサ70が出力する磁気データmは、磁極北に向かう水平成分と伏角方向の鉛直成分とを有する地磁気を表すベクトルの他に、機器に搭載された部品が発する磁界等を表すベクトルも含む値となる。従って、地磁気の値を正確に知るためには、3次元磁気センサが出力するベクトルデータ(磁気データm)から、携帯機器1の部品が発する内部磁界を表すベクトルを取り除く補正処理が必要となる。
このように、検出対象である地磁気の正確な値を得るために、補正処理において、3次元磁気センサ70から出力されるデータから取り除かれるべき内部磁界の値を3次元磁気センサ70のオフセットmOFFと呼ぶ。
なお、地磁気検出部70は、携帯機器1の外部にある外部物が発する磁界についても検出する。しかし、本実施形態では、外部物が発する磁界は無視できる程小さいものとする。
【0023】
3次元加速度センサ80は、X軸加速度センサ81、Y軸加速度センサ82、及びZ軸加速度センサ83を備える。各センサは、ピエゾ抵抗型、静電容量型、熱検知型などどのような検知方式であってもよい。加速度センサI/F84は、各センサからの出力信号をAD変換して加速度データaを出力する。この加速度データaは、携帯機器1に固定された座標系における慣性力と重力との合力を、x軸、y軸及びz軸の3成分を有するベクトルとして示すデータである。したがって、携帯機器1が静止状態または等速直線運動状態にあれば、加速度データaは携帯機器1に固定された座標系において重力加速度の大きさと方向とを示すベクトルデータとなる。
【0024】
3次元角速度センサ90は、X軸角速度センサ91、Y軸角速度センサ92、及びZ軸角速度センサ93を備える。角速度センサI/F94は、各センサからの出力信号をAD変換して角速度データgを出力する。角速度データgは、各軸の回りの角速度を示す3次元のベクトルデータである。なお、角速度データgには、3次元角速度センサ90のオフセットgOFFが重畳する。
【0025】
CPU10は、ROM30に格納されている状態推定プログラム100を実行することによって、動的システムの状態を表す複数の物理量、例えば、携帯機器1の姿勢、3次元磁気センサ70のオフセット、地磁気の強さや伏角等の物理量を推定する。すなわち、携帯機器1は、CPU10が状態推定プログラム100を実行することにより、状態推定装置として機能する。
【0026】
状態推定プログラム100は、初期値生成モジュール110と、カルマンフィルタモジュール120とを備える。カルマンフィルタモジュール120は、カルマンフィルタKFの演算を実行する。
【0027】
[2. カルマンフィルタの観測対象及び推定対象]
一般的に、カルマンフィルタは、動的システムの状態を表す複数の物理量の経時的な変化を推定する状態遷移モデルと、動的システムを観測する複数のセンサが計測する値(観測値)を推定する観測モデルと、を有する。そして、カルマンフィルタは、状態遷移モデルを用いて、ある時刻における動的システムの状態を表す複数の物理量(状態変数)を要素とする状態ベクトルから、単位時間が経過した後の状態ベクトルを推定する。次に、カルマンフィルタは、推定された状態ベクトルに基づいて、動的システムの状態を測定する複数のセンサの出力値を要素とする観測値ベクトルの値を推定する。さらに、推定された観測値ベクトルと、実際のセンサの出力値を要素とする観測値ベクトルとの差分として算出される観測残差に基づいて、推定された状態ベクトルを、実際の値(真値)に近い値へと更新し、更新後の状態ベクトルを出力する。
カルマンフィルタは、以上のような演算を繰り返すことにより、状態ベクトルを構成する複数の状態変数の各々を、実際の物理量を正確に表した値(真値)へと近付ける。
【0028】
本実施形態において、カルマンフィルタKFは、携帯機器1の姿勢q、地磁気の強さr、地磁気の伏角θ、携帯機器1の角速度ω、3次元角速度センサ90のオフセットgOFFの推定値gO、及び3次元磁気センサ70のオフセットmOFFの推定値mOを状態変数として採用し、これらを推定の対象とする。
これらの状態変数を要素とする時刻T=kにおける状態ベクトルxkは、以下の式(1)で表される。なお、各状態変数の右下に付された添え字「k」は、当該状態変数が時刻T=kにおける値であることを表す。
【数1】

【0029】
本実施形態では、姿勢qを、クォータニオンを用いて表現する。クォータニオンとは、物体の姿勢(回転状態)を表す4次元数である。具体的には、地上に固定された座標系(例えば、地上の任意の一点を原点とし、互いに直交する3つの方向、例えば、水平東、水平北、及び鉛直上向きを、それぞれx軸、y軸、及びz軸とする座標系)を定め、当該地上に固定された座標系の各軸と、携帯機器1に固定された座標系の各軸とが一致する姿勢qを基準姿勢と定義し、基準姿勢をq=(0、0、0、1)と表現する。このとき、携帯機器1の任意の姿勢qは、基準姿勢に対して単位ベクトルρの方向を回転軸として角度ψだけ回転した姿勢として表現できる。回転後の姿勢qは、式(2)で与えられる。
【数2】

【0030】
本実施形態におけるカルマンフィルタの観測対象は、3次元磁気センサ70から出力される磁気データm、3次元加速度センサ80から出力される加速度データa、及び3次元角速度センサ90から出力される角速度データgである。観測値ベクトルは、これら磁気データm、加速度データa、及び角速度データgを要素とする。時刻T=kにおける観測値ベクトルykは式(3)で与えられる。
【数3】

【0031】
初期値生成モジュール110は、時刻T=0における状態変数を要素とする初期値INIを算出する。初期値INIは、姿勢qの初期値q0、地磁気の強さrの初期値r0、地磁気の伏角θの初期値θ0、角速度ωの初期値ω0、3次元角速度センサ90のオフセット推定値gOの初期値gO,0、及び3次元磁気センサ70のオフセット推定値mOの初期値mO,0を要素として含む。
初期値INIは、カルマンフィルタの演算によって状態変数がなるべく早く正確な値に収束するような値に適宜設定すればよいが、例えば、以下のような値に設定してもよい。
【0032】
地磁気の強さrの初期値r0、及び地磁気の伏角θの初期値θ0は、例えば、GPS部60から供給される位置情報に基づいて生成することができる。これは、地球上の位置が特定できれば、その位置における地磁気の強さ及び伏角を知ることができるからである。具体的には、ROM30には、位置情報と地磁気の強さ及び伏角とを対応づけて記憶したルックアップテーブルLUT1が格納される。初期値生成モジュール110は、ルックアップテーブルLUT1を参照して、位置情報に対応する地磁気の強さ及び伏角を、地磁気の強さrの初期値r0及び地磁気の伏角θの初期値θ0として設定する。
なお、携帯機器1が衛星からの電波の届かない場所(例えば、地下街)にある場合には、GPS部60から位置情報が得られない。そのような場合には、携帯機器1が使われ得る地域の典型的な値を採用すればよい。その値もルックアップテーブルLUT1に格納されている。初期値生成モジュール110は、位置情報の取得が不能な場合には、典型的な値をルックアップテーブルLUT1から読み出す。例えば、日本で販売された携帯機器1については、明石市の地磁気の強さ及び伏角に基づいて、地磁気の強さrの初期値r0、及び地磁気の伏角θの初期値θ0を算出する。
【0033】
角速度ωの初期値ω0は、例えば、携帯機器1が静止していることを仮定して、「0」に設定する。3次元角速度センサ90のオフセット推定値gOの初期値gO,0は、通常「0」近辺に調整されているため、「0」に設定する。姿勢qの初期値q0に関しては、例えば、携帯機器1が一定方向に向いて静止していることを仮定して、実際の初期姿勢とのずれを小さくするような値を設定する。
【0034】
3次元磁気センサ70のオフセット推定値mOの初期値mO,0は、例えば、時刻T=0の3次元磁気センサ70の観測値m0、姿勢qの初期値q0、携帯機器1を使用する地域の地磁気ベクトルmtypical、及び、式(5)に示す行列B(q)を用いて、以下に示す式(4)で与えられる値に設定する。ここで、行列B(q)は、携帯機器1が姿勢qである場合に、地上に固定された座標系において表現されたベクトルを、携帯機器1に固定された座標系において表現するための座標変換行列である。なお、ROM30には、位置情報と地磁気ベクトルmtypicalとを対応づけて記憶したルックアップテーブルLUT2が記憶されている。初期値生成モジュール110は、GPS部60で生成される位置情報に基づいてルックアップテーブルLUT2を参照して地磁気ベクトルmtypicalを取得し、式(4)を演算することによって、オフセット推定値mOの初期値mO,0を得る。
【数4】

【0035】
初期値生成モジュール110は、以上のようにして生成された姿勢qの初期値q0、地磁気の強さrの初期値r0、地磁気の伏角θの初期値θ0、角速度ωの初期値ω0、3次元角速度センサ90のオフセット推定値gOの初期値gO,0、及び3次元磁気センサ70のオフセット推定値mOの初期値mO,0を要素とするベクトルである初期値INIを生成し、これを出力する。
【0036】
[3. カルマンフィルタによる演算]
次に、本実施形態に係るカルマンフィルタKFによる演算の概要について説明する。
カルマンフィルタKFは、動的システムの状態の経時的な変化を表す状態遷移モデルを用いて、ある時刻(時刻T=k−1)のシステムの状態を示す状態ベクトルxk−1から単位時間が経過した後(時刻T=k)の状態ベクトルxkを推定し、この推定値を、推定された状態ベクトル(推定状態ベクトル)x−kとして出力する。そして、カルマンフィルタKFは、各種センサからの出力を要素とする観測値ベクトルykと状態ベクトルxkとの関係を表す観測モデルを用いて、状態遷移モデルにより推定された状態ベクトルx−kに基づいて観測値ベクトルykを推定し、この推定値を、推定された観測値ベクトル(推定観測値ベクトル)y−kとして出力する。なお、本実施形態のカルマンフィルタKFは、非線形カルマンフィルタであるシグマポイントカルマンフィルタにより構成される。シグマポイントカルマンフィルタとは、状態ベクトルxk−1の周囲に複数のシグマポイントχk−1を設定し、これらの複数のシグマポイントχk−1を状態遷移モデルに適用することで、単位時間経過後のシグマポイントχ−kを推定し、シグマポイントの推定値(推定シグマポイント)χ−kの平均を算出することにより、推定された状態ベクトルx−kを求める演算である。従って、推定された観測値ベクトルy−kは、厳密には、推定された状態ベクトルx−kの周辺に存在する複数のシグマポイントの推定値χ−kに基づいて算出される。
その後、カルマンフィルタKFは、推定された観測値ベクトルy−kと、実際の観測値を要素とする観測値ベクトルykとの差分を観測残差ekとして算出する。また、カルマンフィルタKFは、推定された状態ベクトルx−kと、推定された観測値ベクトルy−kと、に基づいてカルマンゲインKkを算出する。そして、カルマンフィルタKFは、観測残差ekとカルマンゲインKkとを用いて推定された状態ベクトルx−kを更新し、更新後の状態ベクトル(状態ベクトルを更新したベクトル)x+kを算出する。
以上のような状態ベクトルxkの更新を繰り返すカルマンフィルタKFの演算により、状態ベクトルxkを実際の物理量を正確に表した値(真値)に近い正確な値へと近付けることができる。
【0037】
[3.1. カルマンフィルタ演算部の動作の概要]
本実施形態におけるカルマンフィルタKFの状態遷移モデルは以下に示す式(6)で与えられ、観測モデルは以下に示す式(7)で与えられる。本実施形態では、式(6)に現れる関数f及び式(7)に現れる関数hは、非線形の関数である。
【数5】

【0038】
ここで、状態ベクトルxkはn次元のベクトルであり、観測値ベクトルykはm次元のベクトルである。なお、本実施形態では、n=15であり、m=9である。また、式(6)に現れるプロセスノイズuk及び式(7)に現れる観測ノイズvkは0を中心とするガウスノイズである。
式(6)は、時刻T=kにおける状態ベクトルxkが、時刻T=k−1における状態ベクトルxk−1を関数fに代入して得られた値と、時刻T=k−1におけるプロセスノイズuk−1とを加算することにより推定されるものであることを示している。
また、式(7)は、時刻T=kにおける観測値ベクトルykが、時刻T=kにおける状態ベクトルxkを関数hに代入して得られる値と、時刻T=kにおける観測ノイズvkとを加算することにより推定されることを示している。
なお、プロセスノイズukの共分散をQ、観測ノイズvkの共分散をRと表す。
【0039】
時刻T=kにおける観測残差ekは、実際の観測値ベクトルykと、推定された観測値ベクトルy−kとに基づいて定められるベクトルであり、以下に示す式(8)で表される。カルマンフィルタKFは、観測残差ekと、式(9)に示すカルマンゲインKkとを用いて、以下の式(10)に示すように、推定された状態ベクトルx−kを更新し、更新後の状態ベクトルx+kを算出する。また、カルマンフィルタKFは、以下の式(11)に示すように、状態ベクトルxkの推定誤差の共分散Pkを更新する。
なお、P−kは、推定された状態ベクトルx−kの推定誤差の共分散であり、P+kは、更新後の状態ベクトルx+kの推定誤差の共分散である。
また、Pyykは、観測残差ekの共分散であり、Pxykは、推定された状態ベクトルx−kと、推定された観測値ベクトルy−kとの相互共分散行列である。
【数6】

【0040】
観測モデルを用いて推定された観測値ベクトルy−kは、式(7)に示すように、観測モデルを用いて推定された状態ベクトルx−kに基づいて算出される理論値である。よって、観測モデルを用いて推定された観測値ベクトルy−kと実際のセンサ出力に基づく観測値ベクトルykとの差分である観測残差ekは、推定された状態ベクトルx−kと実際の物理量を正確に表した値(真値)との近似度を示す値である。
カルマンフィルタKFは、式(10)に示すように、観測残差ekを用いて、推定された状態ベクトルx−kを、真値に近い更新後の状態ベクトルx+kへと更新する。
【0041】
[3.2. シグマポイントカルマンフィルタによる演算]
本実施形態において、カルマンフィルタKFは、アンセンテッド変換を用いたシグマポイントカルマンフィルタにより構成される。以下では、図3に示すカルマンフィルタKFの機能ブロック図を参照しつつ、カルマンフィルタKFによる演算の詳細を説明する。
【0042】
遅延部121は、加算器132から出力される更新後の状態ベクトルx+kを、単位時間(時刻T=k−1から時刻T=kに相当する時間)だけ遅延させることで、状態ベクトルx+k−1を生成し、これを、シグマポイント生成部122に対して出力する。なお、初回の演算(時刻T=0)では、遅延部121は、初期値生成モジュール110が出力する初期値INIを用いて、状態ベクトルx+k−1を生成する。
また、遅延部121は、減算器133から出力される更新後の状態ベクトルx+kの推定誤差の共分散P+kを単位時間遅延させることで、状態ベクトルx+k−1の推定誤差の共分散P+k−1を生成し、これを、シグマポイント生成部122及び共分散算出部125に対して出力する。
【0043】
シグマポイント生成部122は、状態ベクトルx+k−1に基づいて、a個のシグマポイントχ+k−1(i)(i=1,2,…a)を生成する(aは、2以上の自然数)。シグマポイントχ+k−1(i)の生成は、以下に示す公知の方法を適用する。
シグマポイント生成部122は、まず、状態ベクトルx+k−1の推定誤差の共分散P+k−1から、式(12)に示す共分散P+k−1の平方根を表すn行n列の行列を生成する。次に、シグマポイント生成部122は、共分散P+k−1の平方根を表す行列と、各種係数とに基づいて、a個のシグマポイント算出用ベクトルを定める。シグマポイント算出用ベクトルは、n次元のベクトルである。その後、シグマポイント生成部122は、状態ベクトルx+k−1と、a個のシグマポイント算出用ベクトルとに基づいて、a個のシグマポイントχ+k−1(i)を生成し、これを状態遷移モデル部123に対して出力する。
なお、a個のシグマポイントχ+k−1(i)の生成において用いられる各種係数は、後述する式(14)における重みwiの生成にも用いられる値であり、公知の方法により定められる。また、a個のシグマポイント算出用ベクトルには0ベクトルが含まれていても構わない。
【数7】

【0044】
状態遷移モデル部123は、式(13)に示すように、時刻T=k−1におけるa個のシグマポイントχ+k−1(i)の各々を、状態遷移モデルに適用することにより、時刻T=kにおけるa個のシグマポイントの推定値χ−k(i)を算出する。
【数8】

【0045】
次に、平均算出部124は、式(14)に示すように、時刻T=kにおけるa個のシグマポイントの推定値χ−k(i)の重み付き平均を計算することで、推定された状態ベクトルx−kを算出し、これを出力する。なお、式(14)に現れる重みwiは、シグマポイントχ+k−1(i)の生成において用いられた各種係数に基づいて定められる。
このように、シグマポイント生成部122、状態遷移モデル部123、及び平均算出部124は、状態ベクトルx+k−1から、推定された状態ベクトルx−kを算出する推定状態ベクトル算出部140として機能する。
【数9】

【0046】
共分散算出部125は、推定された状態ベクトルx−kの推定誤差の共分散P−kを算出する。推定された状態ベクトルx−kの推定誤差の共分散P−kは、式(15)に示すように、a個のシグマポイントの推定値χ−k(i)、推定された状態ベクトルx−k、重みwi、及びプロセスノイズuk−1の共分散Qに基づいて算出することができる。
但し、本実施形態では、処理負荷を削減する観点から、共分散P−kのうち一部の成分は、式(15)を用いずに、後述する式(30)に基づいて算出する。この点についての詳細は後述する。
【数10】

【0047】
一方、観測モデル部126は、式(16)に示すように、時刻T=kにおけるa個のシグマポイントの推定値χ−k(i)の各々を、観測モデルに適用することにより、a個の推定観測値γk(i)を算出する。
【数11】

【0048】
そして、平均処理部127は、式(17)に示すように、a個の推定観測値γk(i)の平均を演算することにより、推定された観測値ベクトルy−kを算出する。
このように、シグマポイント生成部122、状態遷移モデル部123、観測モデル部126、及び平均処理部127は、状態ベクトルx+k−1から、推定された観測値ベクトルy−kを算出する推定観測値ベクトル算出部150として機能する。
【数12】

【0049】
次に、平均処理部127は、式(18)に示す観測残差の共分散Pyykを算出する。
【数13】

【0050】
減算器(観測残差生成部)131は、式(8)に示したように、観測値ベクトルykと、推定された観測値ベクトルy−kとの差分として、観測残差ekを算出する。
カルマンゲイン付与部128は、式(19)に示す相互共分散行列Pxykを算出する。次に、カルマンゲイン付与部128は、式(9)に示したように、観測残差の共分散Pyykと、相互共分散行列Pxykとに基づいて、カルマンゲインKkを算出する。その後、カルマンゲイン付与部128は、式(10)の右辺第2項(Kkek)を演算し、その結果を加算器132に対して出力する。
また、カルマンゲイン付与部128は、観測残差の共分散PyykとカルマンゲインKkとに基づいて、式(11)の右辺第2項(KkPyykKTk)を演算し、その結果を減算器133に対して出力する。
【数14】

【0051】
加算器(更新部)132は、式(10)に示したように、推定された状態ベクトルx−kと、カルマンゲイン付与部128から出力される式(10)の右辺第2項(Kkek)と、を加算することにより、更新後の状態ベクトルx+kを算出する。
減算器133は、式(11)に示したように、推定された状態ベクトルx−kの推定誤差の共分散P−kと、カルマンゲイン付与部128から出力される式(11)の右辺第2項(KkPyykKTk)との差分として、更新後の状態ベクトルx+kの推定誤差の共分散P+kを算出する。
【0052】
[3.3. 状態遷移モデル]
次に、状態遷移モデル部123の演算で用いる状態遷移モデルについて説明する。
【0053】
本実施形態に係る状態遷移モデルにおいて、状態ベクトルxkを構成する状態変数のうち、姿勢qについての状態遷移は、式(21)に示す関数fq(q,ω)を用いて、式(20)により定義される。式(20)は、時刻T=kにおける推定された状態ベクトルx−kを構成する状態変数である姿勢q−kが、時刻T=k−1における状態ベクトルx+k−1を構成する状態変数である姿勢q+k−1及び角速度ω+k−1に基づいて推定されることを示している。
式(21)に示す関数fq(q,ω)は、式(6)に示した関数fのうち、姿勢qを算出する部分のみを表した関数である。式(21)の右辺の演算子Ωは、式(22)により定義される。ここで、I3×3は3行3列の単位行列を表し、3次元ベクトルl=(l1,l2,l3)に対して、[l×]という記号を式(23)で定義する。また、測定時間間隔(時刻T=k−1から時刻T=kまでの間隔)をΔtで表したとき、演算子Ωを構成する成分Ψを、式(24)で定義する。
【数15】

【0054】
姿勢qは、クォータニオンで表現されるため、正規化条件||q||=1が満たされる必要がある。しかし、シグマポイントカルマンフィルタを用いて状態ベクトルxkを更新する場合、更新後の状態ベクトルx+kは、式(14)に示すように、シグマポイントの推定値χ−k(i)に重みwiを付与した重み付き平均として算出されるため、(更新前の)状態ベクトルxk−1のノルムと、更新後の状態ベクトルx+kのノルムとは、異なる値となることがある。従って、シグマポイントカルマンフィルタの演算を行う場合、(更新前の)状態ベクトルxk−1の要素である姿勢qk−1のノルムと、更新後の状態ベクトルx+kの要素である姿勢qkのノルムとは、異なる値となる可能性が存在する。つまり、シグマポイントカルマンフィルタの演算を行う場合、姿勢qについての正規化条件が満たされなくなる可能性が存在する。
そこで、姿勢qに対して何らかの演算が行われるときには、演算後の結果をそのベクトル自身の大きさで正規化する。なお、より厳密に正規化条件を保つためには、状態ベクトルxkを構成する要素のうち姿勢qkについてはMRPs (modified Rodrigues parameters)を用いて前時刻との差分情報だけに限定し、カルマンフィルタの外部にある姿勢情報をカルマンフィルタから得られる差分情報に基づいて更新すればよい。
【0055】
地磁気の強さr及び地磁気の伏角θは、変化を予測することが難しい。そこで、本実施形態に係る状態遷移モデルでは、便宜上、時刻T=kにおける地磁気の強さrk及び伏角θkと、時刻T=k−1における地磁気の強さrk−1及び伏角θk−1とは等しい値であるという前提を置く。
同様に、3次元角速度センサ90のオフセット推定値gOも、変化を予測することが難しい。そこで、本実施形態に係る状態遷移モデルでは、便宜上、時刻T=kにおけるオフセット推定値gO,Kと、時刻T=k−1におけるオフセット推定値gO,K−1とは等しい値であるという前提を置く。
【0056】
携帯機器1の角速度ωは、携帯機器1の利用者による携帯機器1の動かし方に依存して変化するため、時刻T=k−1の角速度ωk−1を用いて、時刻T=kにおける角速度ωkを定式化することは難しい。そこで、本実施形態に係る状態遷移モデルでは、便宜上、時刻T=kにおける角速度ωkと、時刻T=k−1における角速度ωk−1とは等しいと仮定する。
【0057】
前述のとおり、3次元磁気センサ70のオフセットmOFFは、携帯機器1の部品が発する内部磁界である。従って、携帯機器1の内部状態が一定である間は、オフセットmOFFも変化しない。一方、携帯機器1の内部状態が変化した場合、例えば、携帯機器1に搭載された部品を流れる電流の大きさが変化した場合や、携帯機器1に搭載された部品の着磁状況が変化した場合には、オフセットmOFFも変化する。すなわち、携帯機器1の内部状態は、携帯機器1の利用者による携帯機器1の操作や、携帯機器1の外部の環境等に依存して変化する。従って、オフセットmOFFが変化するタイミングやオフセットmOFFの変化量を予測することは困難であり、時刻T=k−1におけるオフセット推定値mO,K−1を用いて、時刻T=kにおけるオフセット推定値mO,kを定式化することは難しい。
そこで、本実施形態に係る状態遷移モデルでは、便宜上、時刻T=kにおけるオフセット推定値mO,kと、時刻T=k−1におけるオフセット推定値mO,k−1とは等しいと仮定する。
【0058】
このように、本実施形態に係る状態遷移モデルでは、以下に示す式(25)のように、状態ベクトルxkを構成する状態変数のうち、姿勢q以外は、前の時刻から変化しないという前提を置く。
【数16】

【0059】
ここで、式(1)に示した状態ベクトルxkを、式(26)のように、姿勢qkと、姿勢qk以外の要素を表すベクトルβkとに分離して表現した場合、ベクトルβkについて、式(27)が成立する。すなわち、状態ベクトルx+k−1のうち、姿勢(第2ベクトル)q+k−1以外の要素を表すベクトル(第1ベクトル)β+k−1と、推定された状態ベクトルx−kのうち、姿勢(推定第2ベクトル)q−k以外の要素を表すベクトル(推定第1ベクトル)β−kとは等しい。
【数17】

【0060】
式(27)が成立する場合、式(13)から明らかなように、シグマポイントχ+k−1(i)のうちベクトルβ+k−1に相当する要素と、シグマポイントの推定値χ−k(i)のうちベクトルβ−kに相当する要素とは、等しくなる。
従って、式(27)が成立する場合、状態ベクトルx+k−1の推定誤差の共分散P+k−1のうち、ベクトルβ+k−1の推定誤差の共分散を表す成分と、推定された状態ベクトルx−kの推定誤差の共分散P−kのうち、ベクトルβ−kの推定誤差の共分散を表す成分とは、プロセスノイズuk−1の共分散Qを考慮しなければ、等しいものと看做すことができる(段落[0046]参照)。
【0061】
ここで、共分散Pkを、式(28)に示すように、行列Pqq,k、行列Pqβ,k、行列Pqβ,kT、及び行列Pββ,kの、4つの行列に分割する。行列Pqq,kは、姿勢qkに基づいて定められる、4行4列の行列である。行列Pqβ,kは、姿勢qkとベクトルβkとに基づいて定められる、4行11列の行列である。行列Pββ,kは、ベクトルβkに基づいて定められる、11行11列の行列である。具体的には、行列Pββ,kは、ベクトルβkの推定誤差の共分散を表す行列である。
【数18】

【0062】
また、プロセスノイズukの共分散Qを、式(29)のように、4行4列の行列Qqq、4行11列の行列Qqβ、及び11行11列の行列Qββを用いて表す。
式(6)に示したとおり、プロセスノイズukは、状態ベクトルxkを状態遷移モデルに適用する際に生じるプロセスノイズであり、式(29)に示す共分散Qは、当該プロセスノイズukの共分散を表す。従って、式(29)に現れる、行列Qββは、状態ベクトルxkを状態遷移モデルに適用する際に生じるプロセスノイズのうち、状態ベクトルxkの中で姿勢qk以外の要素を表すベクトルβkに生じるプロセスノイズの共分散を表す。
このとき、行列P−ββ,kは、式(30)に示すように、行列P+ββ,k−1と、行列Qββとの和として定められる。
【数19】

【0063】
共分散P−kの全ての成分を式(15)に基づいて求める場合、n行1列のベクトルと1行n列のベクトルとを乗算してn行n列の行列を求める演算を、a回繰り返すことが必要になる。
一方、式(30)を用いる場合、行列P−ββ,kは、1ステップ前に(時刻T=k−1において)既に算出されている行列P+ββ,k−1と、行列Qββとを単純に加算することにより算出される。そして、共分散P−kは、行列P−ββ,k以外の成分、すなわち、4行4列の行列P−qq,k及び4行11列の行列P−qβ,kのみを、式(15)による演算により求めればよい。この結果、15行15列の共分散P−kの全ての成分を、式(15)を用いて算出する場合に比べて、共分散算出部125における計算量を大幅に低減することが可能となる。
【0064】
なお、状態遷移モデルにおいて、式(25)及び式(27)に示すように、姿勢q以外は、前の時刻から変化しないという前提を置いた場合であっても、状態ベクトルxkは、カルマンフィルタの演算において観測残差ekに基づいて更新される。従って、姿勢qk以外の要素を表すベクトルβkも、カルマンフィルタの演算を繰り返す中で、観測残差ekに基づいて真値に近づくように更新される。
【0065】
[3.4. 観測モデル]
次に、観測モデル部126で行われる演算において用いられる観測モデルについて説明する。
【0066】
3次元角速度センサ90から出力される角速度データgの推定値γgyroは、角速度ωと、3次元角速度センサ90のオフセット推定値gOとを用いて、式(31)で与えられる。
【数20】

【0067】
また、地上に固定された座標系において、地磁気を表すベクトルは、式(32)で与えられる。従って、3次元磁気センサ70から出力される磁気データmの推定値γmagは、3次元磁気センサ70のオフセット推定値mOと、式(5)で示した行列B(q)とを用いて、式(33)で与えられる。
【数21】

【0068】
また、地上に固定された座標系において、重力を表すベクトルを重力加速度で正規化したベクトルは、式(34)で与えられる。従って、3次元加速度センサ80から出力される加速度データaの推定値γaccは、式(5)で示した行列B(q)を用いて、式(35)で与えられる。
【数22】

【0069】
従って、式(3)を式(8)の右辺第1項に代入し、式(31)、式(33)、及び式(35)を用いて式(8)の右辺第2項を表すことにより、式(8)を、以下の式(36)に変形することができる。このとき、観測残差ekは、式(36)により算出される。
【数23】

【0070】
[4. 結論]
以上に示したように、本実施形態に係る状態推定装置は、シグマポイントカルマンフィルタの演算において用いられる状態ベクトルxkを、姿勢qkと、ベクトルβkとに分離して表現し、状態ベクトルx+k−1を構成する要素の一部であるベクトルβ+k−1と、推定された状態ベクトルx−kを構成する要素の一部であるベクトルβ−kとが等しいという前提を置いた。
そして、本実施形態に係る状態推定装置は、推定された状態ベクトルx−kの推定誤差の共分散P−kのうちベクトルβ−kの推定誤差の共分散を表す成分を、状態ベクトルx+k−1の推定誤差の共分散P+k−1のうちベクトルβ+k−1の推定誤差の共分散を表す成分と、プロセスノイズuk−1の共分散Qのうちベクトルβ+k−1に生じるプロセスノイズの共分散を表す成分とを単純に加算することで算出した。
これにより、共分散P−kの全ての成分を式(15)に基づいて求める場合と比較して、シグマポイントカルマンフィルタの計算負荷を大幅に低減することが可能となり、状態推定装置の処理速度の向上、及び携帯機器1の低消費電力化が可能となった。
【0071】
<B.変形例>
本発明は上述した実施形態に限定されるものではなく、例えば、以下の変形が可能である。また、以下に示す変形例のうちの2以上の変形例を組み合わせることもできる。
【0072】
(1)変形例1
上述した実施形態では、状態ベクトルxを構成する要素して、携帯機器1の姿勢q、地磁気の強さr、地磁気の伏角θ、携帯機器1の角速度ω、3次元角速度センサ90のオフセット推定値gO、及び3次元磁気センサ70のオフセット推定値mOを採用し、これら6個の状態変数をカルマンフィルタの演算における推定の対象としたが、本発明はこれに限定されるものでは無い。例えば、状態ベクトルxを、これら6個の状態変数のうちの一部の状態変数により構成し、当該一部の状態変数をカルマンフィルタの演算における推定の対象とするものであってもよい。
【0073】
(2)変形例2
上述した実施形態では、観測値ベクトルyを、3次元磁気センサ70から出力される磁気データm、3次元加速度センサ80から出力される加速度データa、及び3次元角速度センサ90から出力される角速度データgを要素とするベクトルとしたが、本発明はこれに限定されるものでは無く、磁気データm、加速度データa、及び角速度データgのうちの一部のみを利用して観測値ベクトルyを生成してもよい。
【0074】
(3)変形例3
上述した実施形態では、平均算出部124は、式(14)に示すように、推定された状態ベクトルx−kを、a個のシグマポイントの推定値χ−k(i)の重み付き平均として算出したが、本発明はこれに限定されるものではない。
例えば、平均算出部124は、推定された状態ベクトルx−kを構成する要素の一部であるベクトルβ−kを、式(14)を用いず、単純に、状態ベクトルx+k−1を構成する要素の一部であるベクトルβ+k−1と等しい値に設定してもよい。この場合、平均算出部124は、推定された状態ベクトルx−kのうち、姿勢q−kについてのみ、式(14)の重み付き平均を算出する演算により算出する。これにより、15次元のベクトルである推定された状態ベクトルx−kのうち、11次元のベクトルβ−kについては、単純な値の代入により算出することが可能となるため、推定された状態ベクトルx−kの算出に係る処理負荷を、大幅に低減することができる。
【符号の説明】
【0075】
1…携帯機器、KF…カルマンフィルタ、121…遅延部、122…シグマポイント生成部、123…状態遷移モデル部、124…平均算出部、125…共分散算出部、126…観測モデル部、127…平均処理部、127…推定観測値ベクトル算出部、128…カルマンゲイン付与部、131…減算器、132…加算器、133…減算器、140…推定状態ベクトル算出部、150…推定観測値ベクトル算出部、K…カルマンゲイン、xk…状態ベクトル、x−k…推定された状態ベクトル、qk…姿勢、βk…ベクトル、Pk…状態ベクトルの推定誤差の共分散、Q…プロセスノイズの共分散、ek…観測残差、yk…観測値ベクトル、y−k…推定された観測値ベクトル。
【特許請求の範囲】
【請求項1】
第1ベクトル及び第2ベクトルを要素とする状態ベクトルと、前記状態ベクトルの推定誤差の共分散と、に基づいて、状態遷移モデルを用いて、推定第1ベクトル及び推定第2ベクトルを要素とする推定状態ベクトルを算出する推定状態ベクトル算出部と、
前記推定状態ベクトルの推定誤差の共分散を算出する共分散算出部と、
前記状態遷移モデル及び観測モデルを用いて、前記状態ベクトルから、推定観測値ベクトルを算出する推定観測値ベクトル算出部と、
前記推定観測値ベクトルと、外部の複数のセンサから出力される観測値を要素とする観測値ベクトルとに基づいて、観測残差を算出する観測残差生成部と、
前記観測残差と、前記推定状態ベクトルとに基づいて、前記状態ベクトルを更新したベクトルを算出する更新部と、を備え、
前記推定状態ベクトル算出部は、前記推定第1ベクトルを、前記第1ベクトルと等しい値に設定し、
前記共分散算出部は、前記状態ベクトルの推定誤差の共分散のうち、前記第1ベクトルの推定誤差の共分散を表す成分、及び前記状態遷移モデルにおいて前記状態ベクトルに生じるプロセスノイズの共分散のうち、前記第1ベクトルに生じるプロセスノイズの共分散を表す成分を加算して、前記推定状態ベクトルの推定誤差の共分散のうち、前記推定第1ベクトルの推定誤差の共分散を表す成分を算出する、ことを特徴とするカルマンフィルタ。
【請求項2】
前記推定状態ベクトル算出部は、
前記状態ベクトルと、前記状態ベクトルの推定誤差の共分散とに基づいて、複数のシグマポイントを生成するシグマポイント生成部と、
前記状態遷移モデルを用いて、前記複数のシグマポイントから、複数の推定シグマポイントを算出する状態遷移モデル部と、
前記推定状態ベクトルを算出する平均算出部と、を備え、
前記状態遷移モデル部は、
前記推定シグマポイントのうち、前記推定第2ベクトルを算出するために用いられる要素以外の要素を、前記シグマポイントのうち、前記第1ベクトルに基づいて生成された要素と等しい値に設定し、
前記平均算出部は、
前記推定第1ベクトルを、前記第1ベクトルと等しい値に設定し、前記推定第2ベクトルを、前記複数の推定シグマポイントに基づいて算出することを特徴とする、
請求項1に記載のカルマンフィルタ。
【請求項3】
システムを観測して観測値を各々出力する複数のセンサと、請求項1または2に記載のカルマンフィルタとを備えることを特徴とする、状態推定装置。
【請求項4】
システムの状態を推定するカルマンフィルタの制御方法であって、
第1ベクトル及び第2ベクトルを要素とする状態ベクトルと、前記状態ベクトルの推定誤差の共分散と、に基づいて、状態遷移モデルを用いて、推定第1ベクトル及び推定第2ベクトルを要素とする推定状態ベクトルを算出する工程と、
前記推定状態ベクトルの推定誤差の共分散を算出する工程と、
前記状態遷移モデル及び観測モデルを用いて、前記状態ベクトルから、推定観測値ベクトルを算出する工程と、
前記推定観測値ベクトルと、外部の複数のセンサから出力される観測値を要素とする観測値ベクトルとに基づいて、観測残差を算出する工程と、
前記観測残差と、前記推定状態ベクトルとに基づいて、前記状態ベクトルを更新したベクトルを算出する工程と、を備え、
前記推定状態ベクトルを算出する工程は、前記推定第1ベクトルを、前記第1ベクトルと等しい値に設定し、
前記推定状態ベクトルの推定誤差の共分散を算出する工程は、前記状態ベクトルの推定誤差の共分散のうち、前記第1ベクトルの推定誤差の共分散を表す成分、及び前記状態遷移モデルにおいて前記状態ベクトルに生じるプロセスノイズの共分散のうち、前記第1ベクトルに生じるプロセスノイズの共分散を表す成分を加算して、前記推定状態ベクトルの推定誤差の共分散のうち、前記推定第1ベクトルの推定誤差の共分散を表す成分を算出する、ことを特徴とするカルマンフィルタの制御方法。
【請求項5】
システムの状態を推定するカルマンフィルタの制御プログラムであって、
第1ベクトル及び第2ベクトルを要素とする状態ベクトルと、前記状態ベクトルの推定誤差の共分散と、に基づいて、状態遷移モデルを用いて、推定第1ベクトル及び推定第2ベクトルを要素とする推定状態ベクトルを算出する処理と、
前記推定状態ベクトルの推定誤差の共分散を算出する処理と、
前記状態遷移モデル及び観測モデルを用いて、前記状態ベクトルから、推定観測値ベクトルを算出する処理と、
前記推定観測値ベクトルと、外部の複数のセンサから出力される観測値を要素とする観測値ベクトルとに基づいて、観測残差を算出する処理と、
前記観測残差と、前記推定状態ベクトルとに基づいて、前記状態ベクトルを更新したベクトルを算出する処理と、をコンピュータに実行させ、
前記推定状態ベクトルを算出する処理は、前記推定第1ベクトルを、前記第1ベクトルと等しい値に設定し、
前記推定状態ベクトルの推定誤差の共分散を算出する処理は、前記状態ベクトルの推定誤差の共分散のうち、前記第1ベクトルの推定誤差の共分散を表す成分、及び前記状態遷移モデルにおいて前記状態ベクトルに生じるプロセスノイズの共分散のうち、前記第1ベクトルに生じるプロセスノイズの共分散を表す成分を加算して、前記推定状態ベクトルの推定誤差の共分散のうち、前記推定第1ベクトルの推定誤差の共分散を表す成分を算出する、ことを特徴とするカルマンフィルタの制御プログラム。
【請求項1】
第1ベクトル及び第2ベクトルを要素とする状態ベクトルと、前記状態ベクトルの推定誤差の共分散と、に基づいて、状態遷移モデルを用いて、推定第1ベクトル及び推定第2ベクトルを要素とする推定状態ベクトルを算出する推定状態ベクトル算出部と、
前記推定状態ベクトルの推定誤差の共分散を算出する共分散算出部と、
前記状態遷移モデル及び観測モデルを用いて、前記状態ベクトルから、推定観測値ベクトルを算出する推定観測値ベクトル算出部と、
前記推定観測値ベクトルと、外部の複数のセンサから出力される観測値を要素とする観測値ベクトルとに基づいて、観測残差を算出する観測残差生成部と、
前記観測残差と、前記推定状態ベクトルとに基づいて、前記状態ベクトルを更新したベクトルを算出する更新部と、を備え、
前記推定状態ベクトル算出部は、前記推定第1ベクトルを、前記第1ベクトルと等しい値に設定し、
前記共分散算出部は、前記状態ベクトルの推定誤差の共分散のうち、前記第1ベクトルの推定誤差の共分散を表す成分、及び前記状態遷移モデルにおいて前記状態ベクトルに生じるプロセスノイズの共分散のうち、前記第1ベクトルに生じるプロセスノイズの共分散を表す成分を加算して、前記推定状態ベクトルの推定誤差の共分散のうち、前記推定第1ベクトルの推定誤差の共分散を表す成分を算出する、ことを特徴とするカルマンフィルタ。
【請求項2】
前記推定状態ベクトル算出部は、
前記状態ベクトルと、前記状態ベクトルの推定誤差の共分散とに基づいて、複数のシグマポイントを生成するシグマポイント生成部と、
前記状態遷移モデルを用いて、前記複数のシグマポイントから、複数の推定シグマポイントを算出する状態遷移モデル部と、
前記推定状態ベクトルを算出する平均算出部と、を備え、
前記状態遷移モデル部は、
前記推定シグマポイントのうち、前記推定第2ベクトルを算出するために用いられる要素以外の要素を、前記シグマポイントのうち、前記第1ベクトルに基づいて生成された要素と等しい値に設定し、
前記平均算出部は、
前記推定第1ベクトルを、前記第1ベクトルと等しい値に設定し、前記推定第2ベクトルを、前記複数の推定シグマポイントに基づいて算出することを特徴とする、
請求項1に記載のカルマンフィルタ。
【請求項3】
システムを観測して観測値を各々出力する複数のセンサと、請求項1または2に記載のカルマンフィルタとを備えることを特徴とする、状態推定装置。
【請求項4】
システムの状態を推定するカルマンフィルタの制御方法であって、
第1ベクトル及び第2ベクトルを要素とする状態ベクトルと、前記状態ベクトルの推定誤差の共分散と、に基づいて、状態遷移モデルを用いて、推定第1ベクトル及び推定第2ベクトルを要素とする推定状態ベクトルを算出する工程と、
前記推定状態ベクトルの推定誤差の共分散を算出する工程と、
前記状態遷移モデル及び観測モデルを用いて、前記状態ベクトルから、推定観測値ベクトルを算出する工程と、
前記推定観測値ベクトルと、外部の複数のセンサから出力される観測値を要素とする観測値ベクトルとに基づいて、観測残差を算出する工程と、
前記観測残差と、前記推定状態ベクトルとに基づいて、前記状態ベクトルを更新したベクトルを算出する工程と、を備え、
前記推定状態ベクトルを算出する工程は、前記推定第1ベクトルを、前記第1ベクトルと等しい値に設定し、
前記推定状態ベクトルの推定誤差の共分散を算出する工程は、前記状態ベクトルの推定誤差の共分散のうち、前記第1ベクトルの推定誤差の共分散を表す成分、及び前記状態遷移モデルにおいて前記状態ベクトルに生じるプロセスノイズの共分散のうち、前記第1ベクトルに生じるプロセスノイズの共分散を表す成分を加算して、前記推定状態ベクトルの推定誤差の共分散のうち、前記推定第1ベクトルの推定誤差の共分散を表す成分を算出する、ことを特徴とするカルマンフィルタの制御方法。
【請求項5】
システムの状態を推定するカルマンフィルタの制御プログラムであって、
第1ベクトル及び第2ベクトルを要素とする状態ベクトルと、前記状態ベクトルの推定誤差の共分散と、に基づいて、状態遷移モデルを用いて、推定第1ベクトル及び推定第2ベクトルを要素とする推定状態ベクトルを算出する処理と、
前記推定状態ベクトルの推定誤差の共分散を算出する処理と、
前記状態遷移モデル及び観測モデルを用いて、前記状態ベクトルから、推定観測値ベクトルを算出する処理と、
前記推定観測値ベクトルと、外部の複数のセンサから出力される観測値を要素とする観測値ベクトルとに基づいて、観測残差を算出する処理と、
前記観測残差と、前記推定状態ベクトルとに基づいて、前記状態ベクトルを更新したベクトルを算出する処理と、をコンピュータに実行させ、
前記推定状態ベクトルを算出する処理は、前記推定第1ベクトルを、前記第1ベクトルと等しい値に設定し、
前記推定状態ベクトルの推定誤差の共分散を算出する処理は、前記状態ベクトルの推定誤差の共分散のうち、前記第1ベクトルの推定誤差の共分散を表す成分、及び前記状態遷移モデルにおいて前記状態ベクトルに生じるプロセスノイズの共分散のうち、前記第1ベクトルに生じるプロセスノイズの共分散を表す成分を加算して、前記推定状態ベクトルの推定誤差の共分散のうち、前記推定第1ベクトルの推定誤差の共分散を表す成分を算出する、ことを特徴とするカルマンフィルタの制御プログラム。
【図1】


【図2】


【図3】




【図2】


【図3】


【公開番号】特開2013−61309(P2013−61309A)
【公開日】平成25年4月4日(2013.4.4)
【国際特許分類】
【出願番号】特願2011−201544(P2011−201544)
【出願日】平成23年9月15日(2011.9.15)
【出願人】(000004075)ヤマハ株式会社 (5,930)
【Fターム(参考)】
【公開日】平成25年4月4日(2013.4.4)
【国際特許分類】
【出願日】平成23年9月15日(2011.9.15)
【出願人】(000004075)ヤマハ株式会社 (5,930)
【Fターム(参考)】
[ Back to top ]

