ルートi(√i)演算の保持を特徴とする基数8固定小数点FFT論理回路
【課題】 高速フーリエ変換(FFT)演算の丸め誤差を軽減させること。
【解決手段】 バタフライ演算(8p)に含まれる複素平面上の回転因子のうちで、無理数(√、平方根)として現れるデータを意図的に計算することなく、多段にパイプライン化されているFFTの複数の段のうちの1つの段に設けられているメモリに保持(preserve)しておき、後段において再度現れたきたら、2つの回転因子を掛け合わせる演算を行う。このことによって、基数8 (radix-8)のバタフライ演算8p中の丸め誤差を無くすることができる。基数2 (radix-s)または基数4 (radix-4)のバタフライ演算によって、さらなる段を被せるように応用することもできる。
【解決手段】 バタフライ演算(8p)に含まれる複素平面上の回転因子のうちで、無理数(√、平方根)として現れるデータを意図的に計算することなく、多段にパイプライン化されているFFTの複数の段のうちの1つの段に設けられているメモリに保持(preserve)しておき、後段において再度現れたきたら、2つの回転因子を掛け合わせる演算を行う。このことによって、基数8 (radix-8)のバタフライ演算8p中の丸め誤差を無くすることができる。基数2 (radix-s)または基数4 (radix-4)のバタフライ演算によって、さらなる段を被せるように応用することもできる。
【発明の詳細な説明】
【技術分野】
【0001】
本発明は、高速フーリエ変換(FFT)処理の技術に関する。
【背景技術】
【0002】
通信の広帯域化に伴い、より多くの情報に対する複雑な信号処理が必要となっている。例として、OFDM(Orthogonal Frequency Division Multiplexing: 直交周波数分割多重方式)や、FDE(Frequency Domain Equalization: 周波数領域等価)があり、これらの実現にはハードウエアを用いた高スループットのFFTが必要となる。
【0003】
高スループットのFFTのハードウエア実装には、多量のハードウエアリソースが必要となる。また、このFFTの入出力にはADC、DACが用いられるが、広帯域化にともなう動作速度の向上によってADC、DACの有効ビット数ENoB(Effective number of bits)に限りがある。現状求められるFFTの次数、スループット、ADC/DAC のENoB数を記す。
【0004】
・ 512-point(次数N=512)FFT for IEEE802.15.3c ( mmWave )
・ 2.5G symbol per second
・ 8-bit ADC/DAC for 2.5G sps
【0005】
上記の要求を満たし、かつ、回路規模を抑えたFFTの実装を可能とするためには、従来用いられている基数2や基数4より高い基数の基数8 (radix-8)を用いつつ、さらに、演算は固定小数点(jビット、jは自然数)で実装するといった工夫が必要となる。しかし、固定小数点 FFT は演算の際の丸め誤差が増加してしまう問題がある。
【0006】
特許文献1では、その背景に、ローパワー&安価な実装を目的として固定小数点のFFTを考えた場合、量子化誤差が生じることがある。その量子化誤差は、FFT内部でのrotationによって局所的に大きくなり、その大きくなった誤差が 時間領域でのOFDM のCyclic Prefex部分に現れた場合は、送受信したい符号のノイズ元にはなりずらいが、逆にそれ以外の部分に乗るとノイズ元となる。
【0007】
この特許文献1では、周波数領域においては、DC成分にこの誤差が乗った場合エラーが大きくなるが、サブキャリア側であればエラーの影響は少ない。そこで、IFFTしたのちにシンボルをシフトして、量子化誤差の生まれる場所をずらすことで、送受信したい符号へのエラーの影響を少なくする技術を開示している。
【0008】
これに対して、本願発明は、FFT, IFFT内部での量子化誤差を下げる方法であるので、特許文献1の技術とは異なっている。
【0009】
特許文献2では、その背景に、FFTの次数が増えるにつれて、SQNR( signal to quantization noise ratio)が下がって悪影響を及ぼすことがある。悪影響を減らすためには、高次のFFTでは、FFT内部の演算ビット数として長い word長が必要になる。 また、FFT processor では、隣接する複数の入力データの値の有効桁を、隣接する値間で共通の有効桁となるように、隣接する複数のデータ全体で一つの有効桁を持つように実装するblock-floating point が使われる。
【0010】
この特許文献2では、block-floating point を用いて複素乗算回路を減らすために、radix-8 を3ステージに分割(実質 radix-2に展開) してパイプライン動作させる方法を開示している。このことにより回路量は減るが、演算に要するレイテンシは3倍に伸びる。さらに、prefetch buffer と呼ばれる値をキャッシュするバッファを用いて、乗算回数をへらすように(3rd stage) スケジューリングをする方法を開示し、このprefetch buffer を生かして block-floating の正規化を効率よく実装している。
【0011】
しかし、radix-8 での45度回転部分を保持するといった本願発明に相当する技術的思想は無い。
【0012】
特許文献3は、FFTの内部バタフライ演算単位で出力値をオーバーフローしない程度に最大の値を持つようにスケールさせる方法について開示している。比較的一般的な方法と思われるが、本願発明の方式とは異なる部分に関するものである。
【0013】
特許文献4は、UWB用 128ビットFFT の演算を行うハードウエアアーキテクチャであって、butterfly-2のユニット と、radix-8を3-stage化(実質radix-2の組み合わせ)により実現したアーキテクチャが開示されている。非常に特定されたアーキテクチャの開示であって、本願発明の技術的思想は含まれていない。
【0014】
特許文献5は、基数2のバタフライ演算を内部に有する FFT のパイプライン型FFTのアーキテクチャとその動作に関して開示されている。本願発明の基数8に関する特徴とはまったく異なるものである。
【0015】
非特許文献1は、FFTアルゴリズムの代表的なものとして、Cooley-Tukey FFTとして知られているものである。
【先行技術文献】
【特許文献】
【0016】
【特許文献1】WO 2009/142563 A1 METHOD FOR MOVING QUANTIZATION NOISE INTRODUCED IN FIXED-POINT CALCULATION OF FAST FOURIER TRANSFORMS (国際公開公報)
【特許文献2】US 2005/0289207 A1 FAST FOURIER TRANSFORM PROCESSOR, DYNAMIC SCALING METHOD AND FAST FOURIER TRANSFORM WITH RADIX-8 ALGORITHM (米国特許公開公報)
【特許文献3】US 2004/0111227 A1 METHOD AND SYSTEM FOR FIXED POINT FAST FOURIER TRANSFORM WITH IMPROVED SNR (米国特許公開公報)
【特許文献4】US 2006/0282764 A1 HIGH-THROUGHPUT PIPELINED FFT PROCESSOR (米国特許公開公報)
【特許文献5】WO 2007/115329 A2 FFT ARCHITECTURE AND METHOD (国際公開公報)(日本国への国内段階移行後の(日本語による)国内公表 特表2009-535678号公報 パイプラインFFTのアーキテクチャおよび方法)
【非特許文献】
【0017】
【非特許文献1】Cooley, James W., and John W. Tukey, “An algorithm for the machine calculation of complex Fourier series,” Math. Comput. 19, 297?301, 1965
【発明の概要】
【発明が解決しようとする課題】
【0018】
本発明の目的は、FFT演算の丸め誤差を軽減させることにある。
【課題を解決するための手段】
【0019】
基数8 (radix-8)のFFT において、バタフライ演算に含まれる回転の項
【数1】

と
【数2】

を分離し、この数2に含まれる
【数3】

の項をFFT内部で保持して演算を回避することによって、限られた回路で演算誤差を軽減する演算方式および回路構成を実現する。
【0020】
FFT/IFFT の演算の際に入出力間でのpowerの均等化が必要となる状況で、FFTの次数が2の奇数乗
【数4】

の場合には均等化のために
【数5】

倍という演算が必要になる。このFFT/IFFT の振幅変更の際のこの√2(ルート2)倍の演算を本願発明の構成を用いて誤差を軽減して求める。
【0021】
上記の演算方式を用いることによって45度の座標回転の演算や振幅を√2(ルート2)倍にする演算の誤差を軽減可能となるため、その特徴を生かし、通常軸上の constellation として出力する点を、45度回転して振幅を√2 倍することで、座標平面を効率的に利用する。
【発明の効果】
【0022】
本発明により、FFT演算の丸め誤差が軽減される。
【図面の簡単な説明】
【0023】
【図1】図1は、基数2、次数N=8の場合のFFTのバタフライ演算の様子を示す図である。
【図2】図2は、基数8のバタフライ演算(8pと記述)がFFT全体でどのような順番で処理されるかを図示したものである。
【図3】図3は、kが奇数となる回転因子の演算を保持(preserve)する場合の、基数8のバタフライ演算式を示す図である。
【図4】図4は図3で示した式が具体的にどのように構成されるかを示した図である。
【図5】図5は、軸上のシンボルの回転と振幅変更による ADC/DAC無変更での振幅拡大例を示す図である。
【図6】図6は、誤差のヒストグラムを示す図である。
【図7】図7は、S/N比を示す図である。
【発明を実施するための形態】
【0024】
[FFTとDFTの計算誤差]
高速フーリエ変換(FFT: Fast Fourier Transform)とは、離散フーリエ変換(DFT: Discrete Fourier Transform)を高速に演算するアルゴリズムである。次数NのDFTは、
入力を 、
【数6】

出力を
【数7】

とした場合、次の数8で表される。
【数8】

【0025】
この数8のうちの
【数9】

は「回転因子」であり、次数Nの離散フーリエ変換では、入力と回転因子の複素乗算をN回行い、それらN個の複素加算を行う。
【0026】
DFTの計算誤差は、この複素乗算と複素加算によって生じる。Xkを計算するためには、DFTの式をそのまま演算した場合、N回の複素乗算とN回の複素加算が必要となる。
【0027】
浮動小数点演算でDFTを求める場合、仮数部の有効桁数によって乗算、加算のいずれの場合でも丸めによる計算誤差が発生する。固定小数点演算でも同様で、有効桁より小さな値は丸められ、また、有効桁を越える演算結果となった場合はオーバーフローとなり演算結果は最大値に固定され正確な値は得られない。この丸め誤差の最大値は、演算結果を再度演算に用いる回数に比例して増加する。
【0028】
[基数2(radix-2)のFFTおよび計算誤差]
FFTアルゴリズムの代表的なものとしてCooley-Tukey FFT(非特許文献1)が知られており。それは次数NのDFTを
【数10】

の演算量で行う高速化アルゴリズムである。次数の大きなFFTを計算する際に、演算をいくつかの集合に分割して行う方法がとられ、演算の際の集合の入出力数を「基数」と呼び、共通な演算部分を適切に選ぶことで演算の効率化が可能となる。
【0029】
例として、基数2の場合はFFTの演算対象のある2点
【数11】

に対し、数14で示されるバタフライ演算を
【数12】

の段数にわたって繰り返し行うことで演算が行われる。
【0030】
図1は、基数2、次数N=8の場合のFFTのバタフライ演算の様子を示す図である。
【0031】
図の網掛けの部分が以下の数14であらわされるバタフライ演算部であり共通の演算である。
【0032】
バタフライ演算間に現れる
【数13】

は「回転因子」と呼ばれ、入力値を複素平面上で回転する演算を表す。
【数14】

【0033】
FFTの計算誤差は、このバタフライ演算の複素加算と乗算、および回転因子による回転によって生じる。FFTの次数がNの基数2のFFTの場合、あるXk の計算には数11で表した回数のバタフライ演算、および回転因子の回転が行われる。これらの演算は複素加減算、乗算であるため、固定小数点の場合、演算のたびに計算誤差や有効桁操作による丸めが生じる。
【0034】
[基数8(radix-8)のFFTおよび計算誤差]
FFT内部での演算回数(とくに乗算)を減らす方法として、基数をより大きなものにする方法が一般的に知られている。例として、基数8の場合のバタフライ演算に相当する演算を次の数15に示す。基数8のため、一度の演算に扱う入出力は8次元となり、バタフライ演算はマトリックスに回転因子を含むものとして表示される。
【数15】

【0035】
図2は、基数8のバタフライ演算(8pと記述)がFFT全体でどのような順番で処理されるかを図示したものである。図2はFFTの次数 N=512 の場合について図示しており、左側の x がFFTへの入力であり、右側のX が出力である。8pは基数8の演算であるため、配列の次数Nが8のべき乗であり、パイプライン化された配列に、多段の
【数16】

が割り当てられている場合には、k回の8pの演算を行う必要がある。よって、次数N=512のFFTを行うためには、図2のようにある入力xに対して8pが3回適用される。8p演算の間の rotation & bit swap は、回転因子とビットの置換部分である。
【0036】
ここで、8p演算の中の
【数17】

は複素平面上の回転であり、特にkが奇数の場合は無理数となるため丸めの誤差が生じる。N=512 の例では3回の8p演算が行われるため、3回の演算の丸めの誤差が累積することになる。
【0037】
[ルートi(√i)演算保持基数8(radix-8)固定小数点FFT]
本願発明では、この基数8のバタフライ演算の丸め誤差を軽減する方法を開示する。前節において、
【数18】

のkが奇数の場合に無理数となり丸め誤差が生じると述べた。ここでnを整数とした場合、無理数となる数18は
【数19】

で表すことができる。ここで、別の無理数となる数18として
【数20】

を考える。
【0038】
この奇数同士の回転因子の乗算は、次の数21のように変形できる。
【数21】

この数21は、
【数22】

のいずれかの値となり、この演算においては丸め誤差を生じない。
【0039】
この特性を利用して、kが奇数となる 数18を意図的に計算せず、FFTの後段で再度kが奇数となる数18が現れた段階でこれら2つの回転因子を掛け合わせて演算を行うことによって、基数8のバタフライ演算8p中の丸め誤差を無くすというのが、本願発明の方法である。
【0040】
図3は、kが奇数となる回転因子の演算を保持(preserve)する場合の、基数8のバタフライ演算式を示す図である。
【数23】

はkが偶数となる数18(回転因子)によって構成され、
【数24】

はkが奇数となる数18(回転因子)によって構成されている。
【0041】
この数23 、数24(保持しておくもの)が基数8のバタフライ演算のたびに交互に作用し値を交換することで演算が行われる。
【0042】
次に示す、数25、数26のように表現される。
【数25】

【数26】

【0043】
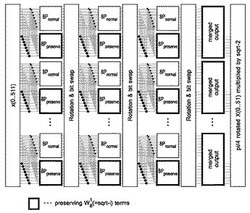
図4は図3で示した式が具体的にどのように構成されるかを示した図である。
【0044】
数23、数24が並列に配置され入力値をそれぞれ処理し、後段へと値を伝播させる。図4の最後にある merged output は、数24はkが奇数となる数18が未処理のまま保持された値を出力しているため、merged output 部分でその未処理の演算を行って数23と適切に足し合わせることにより、最終的なFFTの演算結果を得る。
【0045】
このような構成は、コンピュータに実行させるシステムまたは方法として実現されるが、ハードウエア資源としてのメモリが、または、ハードウエア資源とソフトウエア資源とが協働するソフトウエアとしての配列要素の(仮想)メモリが、「保持」しておくことに利用することができる。
【0046】
[本願発明の応用例(その1)]
本願発明は、基数8のFFTの丸め誤差を減らすものであるが、この構成の特徴を生かす応用例も考えられる。
【0047】
一つ目の応用例として、FFT/IFFT のpowerの均等化がある。FFT/IFFT では、以下の数30のPerseval’s law で示されるような入出力のpower の関係が成り立つ。以下の数30は、入出力の power を均等化する場合、FFTの演算結果の振幅を次数のルートで割る必要があることを意味している。N=512 の場合は、
【数27】

となる。
【数28】

の除算は無理数の演算となるため、通常の演算ではここでも丸め誤差が生じる。
【0048】
本手法ではkが奇数となる数18(回転因子)を保持した構成となっていると述べた。kが奇数の数18(回転因子)は具体的には、実部、虚部がそれぞれ
【数29】

の複素乗算が未処理で保持していることを意味する。
【0049】
よって、上記の power の均等化を行う場合、本方式の数24の出力はすでに 無理数√2で序されていることになる。すなわち、√2の除算を省くことが可能となり、通常のFFT実装に比べ、丸め誤差を軽減できることとなる。
【数30】

【0050】
[本願発明の応用例(その2)]
二つ目の応用例として、BPSKやQPSK等の変調でシンボルを実軸、虚軸に出力する送受信器を考えた場合、意図的にシンボルを45度回転し、振幅を√2倍することによって、ADC/DACの変更無しにシンボルの振幅を大きくすることが出来る。
【0051】
図5は、軸上のシンボルの回転と振幅変更による ADC/DAC無変更での振幅拡大例を示す図である。
【0052】
図5の左の図が軸上にシンボルが配置された場合を表し、ADC・DACの領域の最大間隔Lにシンボルは置かれている。右側は45度回転し振幅を√2(ルート2)倍したものである。振幅が√2倍になっているが ADC/DAC の領域内部にシンボルは配置されている。
【0053】
この45度回転、および振幅√2倍の演算は、第一の例で述べたものと同じ理由から、本手法を用いることによって、回転と振幅√2倍の計算を省くことができる項がある。
【0054】
以上のように、本手法を用いることによって、FFT内部の丸め誤差を軽減するだけではなく、FFTの入出力に関連する45度回転や振幅の√2倍といった演算を除外することができる場合があり、その際の計算誤差を軽減することが可能となる。
【0055】
[本願発明の応用例(その3)]
たとえ次数Nが増えた場合であっても、次数N=512の場合の本願発明を基本に含めれば、基数2(radix-2)のバタフライ演算、または基数4(radix-4)のバタフライ演算を、以下のように被せる形にして応用することができる。
N=1024の場合は、radix-8 - radix-8 - radix-8 - radix-2 の4段構成
N=2048の場合は、radix-8 - radix-8 - radix-8 - radix-2 - radix-2 の5段構成
N=2048の場合は、radix-8 - radix-8 - radix-8 - radix-4 の4段構成
N=4096の場合は、radix-8 - radix-8 - radix-8 - radix-8 の4段構成
すなわち、次数Nが、2のべき乗であるが8のべき乗ではないという場合であっても、演算処理ができる。
【0056】
[本願発明による効果]
本願発明を適用することで、どの程度丸め誤差が軽減されるかに関して検証を行った。比較対象は、十分な精度をもつ浮動小数点演算でFFTを行った場合とし、固定小数点(8ビット)でFFTした場合に生じる誤差に関して、そのヒストグラムとS/N比を求めた。
【0057】
図6は、誤差のヒストグラムを示す図である。
【0058】
図7は、S/N比を示す図である。
【0059】
図6のヒストグラムの横軸は、期待値に対する誤差のベクトル距離であり、例として、期待値が(127,127)に対して得られた値が(130,131) のように誤差を持つ場合、そのベクトル距離は
【数31】

となる。
【0060】
縦軸は、実験により得られた誤差の頻度が全体の何% を占めるかを取ったものである。これらの結果から、本特許を用いない通常の基数8のFFT(図2)では、誤差のベクトル距離の最大が12であるのに比べ、本願発明を用いた場合は5となっていることがわかる。図7はこの結果をS/N比で表したものであり、本願発明を用いることで約6dBの改善が得られる。
【技術分野】
【0001】
本発明は、高速フーリエ変換(FFT)処理の技術に関する。
【背景技術】
【0002】
通信の広帯域化に伴い、より多くの情報に対する複雑な信号処理が必要となっている。例として、OFDM(Orthogonal Frequency Division Multiplexing: 直交周波数分割多重方式)や、FDE(Frequency Domain Equalization: 周波数領域等価)があり、これらの実現にはハードウエアを用いた高スループットのFFTが必要となる。
【0003】
高スループットのFFTのハードウエア実装には、多量のハードウエアリソースが必要となる。また、このFFTの入出力にはADC、DACが用いられるが、広帯域化にともなう動作速度の向上によってADC、DACの有効ビット数ENoB(Effective number of bits)に限りがある。現状求められるFFTの次数、スループット、ADC/DAC のENoB数を記す。
【0004】
・ 512-point(次数N=512)FFT for IEEE802.15.3c ( mmWave )
・ 2.5G symbol per second
・ 8-bit ADC/DAC for 2.5G sps
【0005】
上記の要求を満たし、かつ、回路規模を抑えたFFTの実装を可能とするためには、従来用いられている基数2や基数4より高い基数の基数8 (radix-8)を用いつつ、さらに、演算は固定小数点(jビット、jは自然数)で実装するといった工夫が必要となる。しかし、固定小数点 FFT は演算の際の丸め誤差が増加してしまう問題がある。
【0006】
特許文献1では、その背景に、ローパワー&安価な実装を目的として固定小数点のFFTを考えた場合、量子化誤差が生じることがある。その量子化誤差は、FFT内部でのrotationによって局所的に大きくなり、その大きくなった誤差が 時間領域でのOFDM のCyclic Prefex部分に現れた場合は、送受信したい符号のノイズ元にはなりずらいが、逆にそれ以外の部分に乗るとノイズ元となる。
【0007】
この特許文献1では、周波数領域においては、DC成分にこの誤差が乗った場合エラーが大きくなるが、サブキャリア側であればエラーの影響は少ない。そこで、IFFTしたのちにシンボルをシフトして、量子化誤差の生まれる場所をずらすことで、送受信したい符号へのエラーの影響を少なくする技術を開示している。
【0008】
これに対して、本願発明は、FFT, IFFT内部での量子化誤差を下げる方法であるので、特許文献1の技術とは異なっている。
【0009】
特許文献2では、その背景に、FFTの次数が増えるにつれて、SQNR( signal to quantization noise ratio)が下がって悪影響を及ぼすことがある。悪影響を減らすためには、高次のFFTでは、FFT内部の演算ビット数として長い word長が必要になる。 また、FFT processor では、隣接する複数の入力データの値の有効桁を、隣接する値間で共通の有効桁となるように、隣接する複数のデータ全体で一つの有効桁を持つように実装するblock-floating point が使われる。
【0010】
この特許文献2では、block-floating point を用いて複素乗算回路を減らすために、radix-8 を3ステージに分割(実質 radix-2に展開) してパイプライン動作させる方法を開示している。このことにより回路量は減るが、演算に要するレイテンシは3倍に伸びる。さらに、prefetch buffer と呼ばれる値をキャッシュするバッファを用いて、乗算回数をへらすように(3rd stage) スケジューリングをする方法を開示し、このprefetch buffer を生かして block-floating の正規化を効率よく実装している。
【0011】
しかし、radix-8 での45度回転部分を保持するといった本願発明に相当する技術的思想は無い。
【0012】
特許文献3は、FFTの内部バタフライ演算単位で出力値をオーバーフローしない程度に最大の値を持つようにスケールさせる方法について開示している。比較的一般的な方法と思われるが、本願発明の方式とは異なる部分に関するものである。
【0013】
特許文献4は、UWB用 128ビットFFT の演算を行うハードウエアアーキテクチャであって、butterfly-2のユニット と、radix-8を3-stage化(実質radix-2の組み合わせ)により実現したアーキテクチャが開示されている。非常に特定されたアーキテクチャの開示であって、本願発明の技術的思想は含まれていない。
【0014】
特許文献5は、基数2のバタフライ演算を内部に有する FFT のパイプライン型FFTのアーキテクチャとその動作に関して開示されている。本願発明の基数8に関する特徴とはまったく異なるものである。
【0015】
非特許文献1は、FFTアルゴリズムの代表的なものとして、Cooley-Tukey FFTとして知られているものである。
【先行技術文献】
【特許文献】
【0016】
【特許文献1】WO 2009/142563 A1 METHOD FOR MOVING QUANTIZATION NOISE INTRODUCED IN FIXED-POINT CALCULATION OF FAST FOURIER TRANSFORMS (国際公開公報)
【特許文献2】US 2005/0289207 A1 FAST FOURIER TRANSFORM PROCESSOR, DYNAMIC SCALING METHOD AND FAST FOURIER TRANSFORM WITH RADIX-8 ALGORITHM (米国特許公開公報)
【特許文献3】US 2004/0111227 A1 METHOD AND SYSTEM FOR FIXED POINT FAST FOURIER TRANSFORM WITH IMPROVED SNR (米国特許公開公報)
【特許文献4】US 2006/0282764 A1 HIGH-THROUGHPUT PIPELINED FFT PROCESSOR (米国特許公開公報)
【特許文献5】WO 2007/115329 A2 FFT ARCHITECTURE AND METHOD (国際公開公報)(日本国への国内段階移行後の(日本語による)国内公表 特表2009-535678号公報 パイプラインFFTのアーキテクチャおよび方法)
【非特許文献】
【0017】
【非特許文献1】Cooley, James W., and John W. Tukey, “An algorithm for the machine calculation of complex Fourier series,” Math. Comput. 19, 297?301, 1965
【発明の概要】
【発明が解決しようとする課題】
【0018】
本発明の目的は、FFT演算の丸め誤差を軽減させることにある。
【課題を解決するための手段】
【0019】
基数8 (radix-8)のFFT において、バタフライ演算に含まれる回転の項
【数1】

と
【数2】

を分離し、この数2に含まれる
【数3】

の項をFFT内部で保持して演算を回避することによって、限られた回路で演算誤差を軽減する演算方式および回路構成を実現する。
【0020】
FFT/IFFT の演算の際に入出力間でのpowerの均等化が必要となる状況で、FFTの次数が2の奇数乗
【数4】

の場合には均等化のために
【数5】

倍という演算が必要になる。このFFT/IFFT の振幅変更の際のこの√2(ルート2)倍の演算を本願発明の構成を用いて誤差を軽減して求める。
【0021】
上記の演算方式を用いることによって45度の座標回転の演算や振幅を√2(ルート2)倍にする演算の誤差を軽減可能となるため、その特徴を生かし、通常軸上の constellation として出力する点を、45度回転して振幅を√2 倍することで、座標平面を効率的に利用する。
【発明の効果】
【0022】
本発明により、FFT演算の丸め誤差が軽減される。
【図面の簡単な説明】
【0023】
【図1】図1は、基数2、次数N=8の場合のFFTのバタフライ演算の様子を示す図である。
【図2】図2は、基数8のバタフライ演算(8pと記述)がFFT全体でどのような順番で処理されるかを図示したものである。
【図3】図3は、kが奇数となる回転因子の演算を保持(preserve)する場合の、基数8のバタフライ演算式を示す図である。
【図4】図4は図3で示した式が具体的にどのように構成されるかを示した図である。
【図5】図5は、軸上のシンボルの回転と振幅変更による ADC/DAC無変更での振幅拡大例を示す図である。
【図6】図6は、誤差のヒストグラムを示す図である。
【図7】図7は、S/N比を示す図である。
【発明を実施するための形態】
【0024】
[FFTとDFTの計算誤差]
高速フーリエ変換(FFT: Fast Fourier Transform)とは、離散フーリエ変換(DFT: Discrete Fourier Transform)を高速に演算するアルゴリズムである。次数NのDFTは、
入力を 、
【数6】

出力を
【数7】

とした場合、次の数8で表される。
【数8】

【0025】
この数8のうちの
【数9】

は「回転因子」であり、次数Nの離散フーリエ変換では、入力と回転因子の複素乗算をN回行い、それらN個の複素加算を行う。
【0026】
DFTの計算誤差は、この複素乗算と複素加算によって生じる。Xkを計算するためには、DFTの式をそのまま演算した場合、N回の複素乗算とN回の複素加算が必要となる。
【0027】
浮動小数点演算でDFTを求める場合、仮数部の有効桁数によって乗算、加算のいずれの場合でも丸めによる計算誤差が発生する。固定小数点演算でも同様で、有効桁より小さな値は丸められ、また、有効桁を越える演算結果となった場合はオーバーフローとなり演算結果は最大値に固定され正確な値は得られない。この丸め誤差の最大値は、演算結果を再度演算に用いる回数に比例して増加する。
【0028】
[基数2(radix-2)のFFTおよび計算誤差]
FFTアルゴリズムの代表的なものとしてCooley-Tukey FFT(非特許文献1)が知られており。それは次数NのDFTを
【数10】

の演算量で行う高速化アルゴリズムである。次数の大きなFFTを計算する際に、演算をいくつかの集合に分割して行う方法がとられ、演算の際の集合の入出力数を「基数」と呼び、共通な演算部分を適切に選ぶことで演算の効率化が可能となる。
【0029】
例として、基数2の場合はFFTの演算対象のある2点
【数11】

に対し、数14で示されるバタフライ演算を
【数12】

の段数にわたって繰り返し行うことで演算が行われる。
【0030】
図1は、基数2、次数N=8の場合のFFTのバタフライ演算の様子を示す図である。
【0031】
図の網掛けの部分が以下の数14であらわされるバタフライ演算部であり共通の演算である。
【0032】
バタフライ演算間に現れる
【数13】

は「回転因子」と呼ばれ、入力値を複素平面上で回転する演算を表す。
【数14】

【0033】
FFTの計算誤差は、このバタフライ演算の複素加算と乗算、および回転因子による回転によって生じる。FFTの次数がNの基数2のFFTの場合、あるXk の計算には数11で表した回数のバタフライ演算、および回転因子の回転が行われる。これらの演算は複素加減算、乗算であるため、固定小数点の場合、演算のたびに計算誤差や有効桁操作による丸めが生じる。
【0034】
[基数8(radix-8)のFFTおよび計算誤差]
FFT内部での演算回数(とくに乗算)を減らす方法として、基数をより大きなものにする方法が一般的に知られている。例として、基数8の場合のバタフライ演算に相当する演算を次の数15に示す。基数8のため、一度の演算に扱う入出力は8次元となり、バタフライ演算はマトリックスに回転因子を含むものとして表示される。
【数15】

【0035】
図2は、基数8のバタフライ演算(8pと記述)がFFT全体でどのような順番で処理されるかを図示したものである。図2はFFTの次数 N=512 の場合について図示しており、左側の x がFFTへの入力であり、右側のX が出力である。8pは基数8の演算であるため、配列の次数Nが8のべき乗であり、パイプライン化された配列に、多段の
【数16】

が割り当てられている場合には、k回の8pの演算を行う必要がある。よって、次数N=512のFFTを行うためには、図2のようにある入力xに対して8pが3回適用される。8p演算の間の rotation & bit swap は、回転因子とビットの置換部分である。
【0036】
ここで、8p演算の中の
【数17】

は複素平面上の回転であり、特にkが奇数の場合は無理数となるため丸めの誤差が生じる。N=512 の例では3回の8p演算が行われるため、3回の演算の丸めの誤差が累積することになる。
【0037】
[ルートi(√i)演算保持基数8(radix-8)固定小数点FFT]
本願発明では、この基数8のバタフライ演算の丸め誤差を軽減する方法を開示する。前節において、
【数18】

のkが奇数の場合に無理数となり丸め誤差が生じると述べた。ここでnを整数とした場合、無理数となる数18は
【数19】

で表すことができる。ここで、別の無理数となる数18として
【数20】

を考える。
【0038】
この奇数同士の回転因子の乗算は、次の数21のように変形できる。
【数21】

この数21は、
【数22】

のいずれかの値となり、この演算においては丸め誤差を生じない。
【0039】
この特性を利用して、kが奇数となる 数18を意図的に計算せず、FFTの後段で再度kが奇数となる数18が現れた段階でこれら2つの回転因子を掛け合わせて演算を行うことによって、基数8のバタフライ演算8p中の丸め誤差を無くすというのが、本願発明の方法である。
【0040】
図3は、kが奇数となる回転因子の演算を保持(preserve)する場合の、基数8のバタフライ演算式を示す図である。
【数23】

はkが偶数となる数18(回転因子)によって構成され、
【数24】

はkが奇数となる数18(回転因子)によって構成されている。
【0041】
この数23 、数24(保持しておくもの)が基数8のバタフライ演算のたびに交互に作用し値を交換することで演算が行われる。
【0042】
次に示す、数25、数26のように表現される。
【数25】

【数26】

【0043】
図4は図3で示した式が具体的にどのように構成されるかを示した図である。
【0044】
数23、数24が並列に配置され入力値をそれぞれ処理し、後段へと値を伝播させる。図4の最後にある merged output は、数24はkが奇数となる数18が未処理のまま保持された値を出力しているため、merged output 部分でその未処理の演算を行って数23と適切に足し合わせることにより、最終的なFFTの演算結果を得る。
【0045】
このような構成は、コンピュータに実行させるシステムまたは方法として実現されるが、ハードウエア資源としてのメモリが、または、ハードウエア資源とソフトウエア資源とが協働するソフトウエアとしての配列要素の(仮想)メモリが、「保持」しておくことに利用することができる。
【0046】
[本願発明の応用例(その1)]
本願発明は、基数8のFFTの丸め誤差を減らすものであるが、この構成の特徴を生かす応用例も考えられる。
【0047】
一つ目の応用例として、FFT/IFFT のpowerの均等化がある。FFT/IFFT では、以下の数30のPerseval’s law で示されるような入出力のpower の関係が成り立つ。以下の数30は、入出力の power を均等化する場合、FFTの演算結果の振幅を次数のルートで割る必要があることを意味している。N=512 の場合は、
【数27】

となる。
【数28】

の除算は無理数の演算となるため、通常の演算ではここでも丸め誤差が生じる。
【0048】
本手法ではkが奇数となる数18(回転因子)を保持した構成となっていると述べた。kが奇数の数18(回転因子)は具体的には、実部、虚部がそれぞれ
【数29】

の複素乗算が未処理で保持していることを意味する。
【0049】
よって、上記の power の均等化を行う場合、本方式の数24の出力はすでに 無理数√2で序されていることになる。すなわち、√2の除算を省くことが可能となり、通常のFFT実装に比べ、丸め誤差を軽減できることとなる。
【数30】

【0050】
[本願発明の応用例(その2)]
二つ目の応用例として、BPSKやQPSK等の変調でシンボルを実軸、虚軸に出力する送受信器を考えた場合、意図的にシンボルを45度回転し、振幅を√2倍することによって、ADC/DACの変更無しにシンボルの振幅を大きくすることが出来る。
【0051】
図5は、軸上のシンボルの回転と振幅変更による ADC/DAC無変更での振幅拡大例を示す図である。
【0052】
図5の左の図が軸上にシンボルが配置された場合を表し、ADC・DACの領域の最大間隔Lにシンボルは置かれている。右側は45度回転し振幅を√2(ルート2)倍したものである。振幅が√2倍になっているが ADC/DAC の領域内部にシンボルは配置されている。
【0053】
この45度回転、および振幅√2倍の演算は、第一の例で述べたものと同じ理由から、本手法を用いることによって、回転と振幅√2倍の計算を省くことができる項がある。
【0054】
以上のように、本手法を用いることによって、FFT内部の丸め誤差を軽減するだけではなく、FFTの入出力に関連する45度回転や振幅の√2倍といった演算を除外することができる場合があり、その際の計算誤差を軽減することが可能となる。
【0055】
[本願発明の応用例(その3)]
たとえ次数Nが増えた場合であっても、次数N=512の場合の本願発明を基本に含めれば、基数2(radix-2)のバタフライ演算、または基数4(radix-4)のバタフライ演算を、以下のように被せる形にして応用することができる。
N=1024の場合は、radix-8 - radix-8 - radix-8 - radix-2 の4段構成
N=2048の場合は、radix-8 - radix-8 - radix-8 - radix-2 - radix-2 の5段構成
N=2048の場合は、radix-8 - radix-8 - radix-8 - radix-4 の4段構成
N=4096の場合は、radix-8 - radix-8 - radix-8 - radix-8 の4段構成
すなわち、次数Nが、2のべき乗であるが8のべき乗ではないという場合であっても、演算処理ができる。
【0056】
[本願発明による効果]
本願発明を適用することで、どの程度丸め誤差が軽減されるかに関して検証を行った。比較対象は、十分な精度をもつ浮動小数点演算でFFTを行った場合とし、固定小数点(8ビット)でFFTした場合に生じる誤差に関して、そのヒストグラムとS/N比を求めた。
【0057】
図6は、誤差のヒストグラムを示す図である。
【0058】
図7は、S/N比を示す図である。
【0059】
図6のヒストグラムの横軸は、期待値に対する誤差のベクトル距離であり、例として、期待値が(127,127)に対して得られた値が(130,131) のように誤差を持つ場合、そのベクトル距離は
【数31】

となる。
【0060】
縦軸は、実験により得られた誤差の頻度が全体の何% を占めるかを取ったものである。これらの結果から、本特許を用いない通常の基数8のFFT(図2)では、誤差のベクトル距離の最大が12であるのに比べ、本願発明を用いた場合は5となっていることがわかる。図7はこの結果をS/N比で表したものであり、本願発明を用いることで約6dBの改善が得られる。
【特許請求の範囲】
【請求項1】
配列の次数Nが8のべき乗である、パイプライン化された配列に、多段の
【数1】

段が割り当てられており、多段のうちの1つの段において処理結果を保持しておくメモリが設けられており、メモリの入力値を基数8(radix−8)のDFTで演算を行い出力値を得て、入力値および出力値の各々が固定小数点型(jビット、jは自然数)で表現されている、離散フーリエ変換(DFT)論理の処理をする計算システムであって、
パイプライン化された配列中の所定の段において、8つの入力(x0〜x7)から処理されるバタフライ演算(8p)に含まれる(複素平面上の)回転因子のうちで無理数として現れるデータを、多段のうちの1つの段に設けられているメモリに保持しておくステップと、
パイプライン化された配列中の(1つの段よりも)後の段において、8つの入力(x0〜x7)から処理されるバタフライ演算(8p)に含まれる(複素平面上の)回転因子のうちで無理数として現れるデータを、前記メモリに保持しておいたデータと掛け合わせることによって、無理数でない(有理数としての)計算データを得るステップとを
コンピュータに実行させる、
前記システム。
【請求項2】
前記無理数が、√(平方根)であることを特徴とする
請求項1に記載のシステム。
【請求項3】
基数8のバタフライ演算(8p)に含まれる複素平面上の回転因子が、
【数2】

であって、kが奇数の場合である
請求項1に記載のシステム。
【請求項4】
前記バタフライ演算(8p)が、
【数3】

である、
請求項1に記載のシステム。
【請求項5】
次数Nが、2のべき乗であるが8のべき乗ではない場合に、さらに基数2(radix−2)または基数4(radix−4)のバタフライ演算による段が被せられる、
請求項1に記載のシステム。
【請求項6】
配列の次数Nが8のべき乗である、パイプライン化された配列に、多段の
【数4】

段が割り当てられており、多段のうちの1つの段において処理結果を保持しておくメモリが設けられており、メモリの入力値を基数8(radix−8)のDFTで演算を行い出力値を得て、入力値および出力値の各々が固定小数点型(jビット、jは自然数)で表現されている、離散フーリエ変換(DFT)論理の処理をする計算の方法であって、
パイプライン化された配列中の所定の段において、8つの入力(x0〜x7)から処理されるバタフライ演算(8p)に含まれる(複素平面上の)回転因子のうちで無理数として現れるデータを、多段のうちの1つの段に設けられているメモリに保持しておくステップと、
パイプライン化された配列中の(1つの段よりも)後の段において、8つの入力(x0〜x7)から処理されるバタフライ演算(8p)に含まれる(複素平面上の)回転因子のうちで無理数として現れるデータを、前記メモリに保持しておいたデータと掛け合わせることによって、無理数でない(有理数としての)計算データを得るステップとを
コンピュータに実行させる、
前記方法。
【請求項7】
前記無理数が、√(平方根)であることを特徴とする
請求項6に記載の方法。
【請求項8】
基数8のバタフライ演算(8p)に含まれる複素平面上の回転因子が、
【数5】

であって、kが奇数の場合である
請求項6に記載の方法。
【請求項9】
前記バタフライ演算(8p)が、
【数6】

である、
請求項6に記載の方法。
【請求項10】
次数Nが、2のべき乗であるが8のべき乗ではない場合に、さらに基数2(radix−2)または基数4(radix−4)のバタフライ演算による段が被せられる、
請求項6に記載の方法。
【請求項1】
配列の次数Nが8のべき乗である、パイプライン化された配列に、多段の
【数1】

段が割り当てられており、多段のうちの1つの段において処理結果を保持しておくメモリが設けられており、メモリの入力値を基数8(radix−8)のDFTで演算を行い出力値を得て、入力値および出力値の各々が固定小数点型(jビット、jは自然数)で表現されている、離散フーリエ変換(DFT)論理の処理をする計算システムであって、
パイプライン化された配列中の所定の段において、8つの入力(x0〜x7)から処理されるバタフライ演算(8p)に含まれる(複素平面上の)回転因子のうちで無理数として現れるデータを、多段のうちの1つの段に設けられているメモリに保持しておくステップと、
パイプライン化された配列中の(1つの段よりも)後の段において、8つの入力(x0〜x7)から処理されるバタフライ演算(8p)に含まれる(複素平面上の)回転因子のうちで無理数として現れるデータを、前記メモリに保持しておいたデータと掛け合わせることによって、無理数でない(有理数としての)計算データを得るステップとを
コンピュータに実行させる、
前記システム。
【請求項2】
前記無理数が、√(平方根)であることを特徴とする
請求項1に記載のシステム。
【請求項3】
基数8のバタフライ演算(8p)に含まれる複素平面上の回転因子が、
【数2】

であって、kが奇数の場合である
請求項1に記載のシステム。
【請求項4】
前記バタフライ演算(8p)が、
【数3】

である、
請求項1に記載のシステム。
【請求項5】
次数Nが、2のべき乗であるが8のべき乗ではない場合に、さらに基数2(radix−2)または基数4(radix−4)のバタフライ演算による段が被せられる、
請求項1に記載のシステム。
【請求項6】
配列の次数Nが8のべき乗である、パイプライン化された配列に、多段の
【数4】

段が割り当てられており、多段のうちの1つの段において処理結果を保持しておくメモリが設けられており、メモリの入力値を基数8(radix−8)のDFTで演算を行い出力値を得て、入力値および出力値の各々が固定小数点型(jビット、jは自然数)で表現されている、離散フーリエ変換(DFT)論理の処理をする計算の方法であって、
パイプライン化された配列中の所定の段において、8つの入力(x0〜x7)から処理されるバタフライ演算(8p)に含まれる(複素平面上の)回転因子のうちで無理数として現れるデータを、多段のうちの1つの段に設けられているメモリに保持しておくステップと、
パイプライン化された配列中の(1つの段よりも)後の段において、8つの入力(x0〜x7)から処理されるバタフライ演算(8p)に含まれる(複素平面上の)回転因子のうちで無理数として現れるデータを、前記メモリに保持しておいたデータと掛け合わせることによって、無理数でない(有理数としての)計算データを得るステップとを
コンピュータに実行させる、
前記方法。
【請求項7】
前記無理数が、√(平方根)であることを特徴とする
請求項6に記載の方法。
【請求項8】
基数8のバタフライ演算(8p)に含まれる複素平面上の回転因子が、
【数5】

であって、kが奇数の場合である
請求項6に記載の方法。
【請求項9】
前記バタフライ演算(8p)が、
【数6】

である、
請求項6に記載の方法。
【請求項10】
次数Nが、2のべき乗であるが8のべき乗ではない場合に、さらに基数2(radix−2)または基数4(radix−4)のバタフライ演算による段が被せられる、
請求項6に記載の方法。
【図4】


【図6】


【図7】


【図1】


【図2】


【図3】


【図5】




【図6】


【図7】


【図1】


【図2】


【図3】


【図5】


【公開番号】特開2012−123561(P2012−123561A)
【公開日】平成24年6月28日(2012.6.28)
【国際特許分類】
【出願番号】特願2010−272947(P2010−272947)
【出願日】平成22年12月7日(2010.12.7)
【出願人】(390009531)インターナショナル・ビジネス・マシーンズ・コーポレーション (4,084)
【氏名又は名称原語表記】INTERNATIONAL BUSINESS MASCHINES CORPORATION
【Fターム(参考)】
【公開日】平成24年6月28日(2012.6.28)
【国際特許分類】
【出願日】平成22年12月7日(2010.12.7)
【出願人】(390009531)インターナショナル・ビジネス・マシーンズ・コーポレーション (4,084)
【氏名又は名称原語表記】INTERNATIONAL BUSINESS MASCHINES CORPORATION
【Fターム(参考)】
[ Back to top ]

