位相情報を用いた高分解能距離測定方法及び距離測定装置
【課題】FFT演算におけるデータ長に依存することなく、高い分解能で効率よく距離測定することができ、コストアップを避けることが可能となり、省電力化や装置の小型化も実現できる高分解能距離測定方法及び距離測定装置を提供せんとする。
【解決手段】周波数解析手段が、定在波又は混合波を周波数の変化分の関数としてフーリエ変換を行うことにより、距離変数を含まない位相項を有する距離スペクトルを算出し、距離スペクトルのピーク付近の位相(位相差)が一定であり、ターゲットの距離に比例した値とした。周波数解析は、複数の異なる中心周波数に基づいてそれぞれ距離スペクトルを算出し、その位相差に基づき、ターゲットまでの距離を求める。
【解決手段】周波数解析手段が、定在波又は混合波を周波数の変化分の関数としてフーリエ変換を行うことにより、距離変数を含まない位相項を有する距離スペクトルを算出し、距離スペクトルのピーク付近の位相(位相差)が一定であり、ターゲットの距離に比例した値とした。周波数解析は、複数の異なる中心周波数に基づいてそれぞれ距離スペクトルを算出し、その位相差に基づき、ターゲットまでの距離を求める。
【発明の詳細な説明】
【技術分野】
【0001】
本発明は、ターゲット(測定対象)までの距離を非接触で測定できる距離測定方法及び装置に関するものである。
【背景技術】
【0002】
この種の非接触距離測定方法としては、例えばマイクロ波、ミリ波レーダの方式としてパルス、FMCW、周波数拡散などのタイプがこれまで研究開発されてきた。特に、FMCWレーダは、比較的簡素な構成で実用的な距離測定性能が実現できることから様々な用途に使用されている。一方、これらとは別のタイプのレーダとして、送信波と受信波を分離せずその干渉により生ずる定在波を利用して距離測定を行うレーダがある(例えば、特許文献1、2参照。)。このレーダは非常に簡素な構成でありながら比較的精度のよい距離測定が可能であり、0mからの距離測定も可能となっている。更に、定在波を利用することなく送信波と受信波の混合波を解析して算出方法も提案されている(特許文献3)。
【0003】
上記特許文献1乃至3に記載の従来の手法において、距離スペクトルはフーリエ変換など周波数スペクトル解析手段によって求めるものとなっている。現実の装置においてフーリエ変換は、FFT(高速フーリエ変換)演算によって実行される。よってレーダの分解能は、距離スペクトル算出前の検出波電力値のデータサンプル数、つまり被変換データ長と、FFT演算におけるデータ長に依存するが、レベル計などの用途においては、数ミリ単位の分解能が要求される。上記特許文献1乃至3に記載の従来の手法においては、位相が距離変数xに依存し、特に特許文献1の手法においては、位相差が距離スペクトルのピーク付近で距離に対して変化し、ターゲットの距離で零となる。これにより、零クロス点を探索する手法となる。しかしながら、零クロス点を正確に探すためには距離スペクトルを細かく計算する必要があり、そのためにはFFT演算におけるデータ長を大きくする必要がある。その結果、計算量が増え、処理速度が遅くなってしまう。あるいは、高価な演算装置の使用が避けられず、コストアップになり、省電力化や装置の小型化への要求にも十分応えられない。
【0004】
高価な演算装置の使用を避け、現実的なコストや処理速度の範囲で算出するとなると、分解能を上げることができず、測定精度を出すことができない。例えば、周波数範囲fw=75MHz、被変換データ長が256点に対してFFT演算におけるデータ長が1024点の場合、分解能は0.5mとなる。同条件で1mmの分解能を得るためには、FFT演算におけるデータ長が512000点以上必要となり、上記のとおりコストアップが避けられず、このような距離測定装置を提供することは現実的には不可能であった。
【先行技術文献】
【特許文献】
【0005】
【特許文献1】国際公開第03/104841号パンフレット
【特許文献2】特開2002−357656号公報
【特許文献3】特開2007−93576号公報
【発明の概要】
【発明が解決しようとする課題】
【0006】
そこで、本発明が前述の状況に鑑み、解決しようとするところは、高い分解能で効率よく距離測定することができ、コストアップを避けることが可能となり、省電力化や装置の小型化も実現できる高分解能距離測定方法及び距離測定装置を提供する点にある。
【課題を解決するための手段】
【0007】
本発明者は、前述の課題解決のため、鋭意検討を重ねた結果、従来の手法は距離スペクトルを求めるときに位相が距離変数xに依存し、位相差が距離スペクトルのピーク付近で距離に対して変化し、このためターゲットの距離で零となる零クロス点を探索する必要があるのであり、この零クロス点を正確に探すために、FFT演算におけるデータ長を大きくし、距離スペクトルを細かく計算する必要が生じていたという点に着眼し、このような零クロス点の探索を不要とし、より高い分解能で効率よく算出できる新たな手法を見い出し、本発明を完成するに至ったものである。
【0008】
すなわち本発明は、信号源から進行波を発生させる手順と、進行波と進行波がターゲットで反射した反射波とが干渉して発生する定在波、或いは進行波と反射波との混合波を検出する手順と、当該定在波又は混合波の周波数解析により、距離スペクトルを算出する手順と、該距離スペクトルの位相情報から、ターゲットまでの距離を求める手順とを備える距離測定方法であって、前記周波数解析が、定在波又は混合波を周波数の変化分の関数としてフーリエ変換を行うことにより、距離変数を含まない位相項を有する距離スペクトルを算出してなることを特徴とする位相情報を用いた高分解能距離測定方法を提供する。
【0009】
ここで、前記周波数解析が、複数の異なる中心周波数に基づいてそれぞれ距離スペクトルを算出し、その位相差に基づき、ターゲットまでの距離を求めることが好ましい。
【0010】
また本発明は、信号源から進行波を発生させる進行波発生手段と、進行波と進行波がターゲットで反射した反射波とが干渉して発生する定在波、或いは進行波と反射波との混合波を検出する検出手段と、当該定在波又は混合波の周波数解析により、距離スペクトルを算出する周波数解析手段と、該距離スペクトルの位相情報から、ターゲットまでの距離を求める距離算出手段とを備え、前記周波数解析手段が、定在波又は混合波を周波数の変化分の関数としてフーリエ変換を行い、距離変数を含まない位相項を有する距離スペクトルを算出してなることを特徴とする位相情報を用いた高分解能距離測定装置をも提供する。
【発明の効果】
【0011】
以上にしてなる本願発明に係る高分解能距離測定方法及び装置によれば、周波数解析のときに定在波又は混合波を周波数の変化分の関数としてフーリエ変換を行うことにより、距離変数を含まない位相項を有する距離スペクトルを算出したので、算出される距離スペクトルのピーク付近の位相(位相差)が一定となり、かつ、ターゲットの距離に比例した値となることから、従来のようにFFT演算におけるデータ長を大きくし、距離スペクトルを細かく計算し、零クロス点を探索するといった処理を経ることなく、位相情報から直接、高分解能で精度よく距離が算出される。したがって、計算量も少なくて済み、算出速度が向上するので、コストアップを避け、省電力化や装置の小型化を実現することもできる。
【0012】
また、周波数解析として、複数の異なる中心周波数に基づいてそれぞれ距離スペクトルを算出し、その位相差に基づき、ターゲットまでの距離を求めたので、計測レンジを測りたい距離にあわせて距離を測定することができる。
【図面の簡単な説明】
【0013】
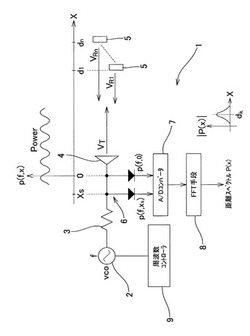
【図1】本発明に係る高分解能距離測定装置の構成を示す概略説明図。
【図2】第2実施形態における送信波であるリニアFM信号を示す説明図。
【図3】解析信号pa(fd)を示す説明図。
【図4】同じく解析信号pa(fd)を示す説明図。
【図5】実施例1のシングルターゲットのシミュレーション結果を示すグラフ
【図6】図5の0m〜5mの間を拡大したグラフ。
【図7】比較例1のシングルターゲットのシミュレーション結果を示すグラフ。
【図8】図7の0m〜5mの間を拡大したグラフ。
【図9】実施例1の複数ターゲットのシミュレーション結果を示す説明図。
【図10】比較例1の複数ターゲットのシミュレーション結果を示す説明図。
【発明を実施するための形態】
【0014】
次に、本発明の実施形態を添付図面に基づき詳細に説明する。
【0015】
尚、以下の説明においては、進行波と反射波が干渉してなる定在波を検出し、これに基づき距離を測定する方法を代表例(第1実施形態)として、その算出原理などについて述べるが、第2実施形態として説明するように、進行波と反射波の混合波を検出してこれに基づき距離を算出する方法も同様に採用できる。また、ターゲット5が複数の場合について説明したが、勿論一つのみの場合であっても同様である。
【0016】
本発明に係る高分解能距離測定装置1は、図1に示すように、信号源から進行波VTを発生させる進行波発生手段として、高周波の電気信号を発生する電圧制御発振器2(VOC(Voltage Controlled Oscillator))、これを電力増幅やインピーダンス整合を行う伝送系3、周波数コントローラ9、及びアンテナ4が設けられている。電圧制御発振器2の発振周波数は、周波数コントローラ9から与えられる制御電圧で変化させられる。本例では、送信波(進行波)の周波数は段階的に切り替えられる。またアンテナ4は、供給される高周波の電気信号を電磁波に変換して周囲の空間に進行波VTを送信する。
【0017】
本例では、アンテナ4から送信される電磁波の進行方向でd1,d2,…,dnの距離に、測定対象となるターゲット5,…が複数存在しており、各ターゲットに入射する進行波VTと、各ターゲットからの反射波VR1,VR2,…,VRNの干渉により定在波が生じる。進行波VTと、進行波VTがターゲット5,…で反射した反射波VR1,VR2,…,VRNとが干渉して発生する定在波を検出する検出手段として、同じくアンテナ4と検波器(Power Detector)6が設けられており、アンテナ4で定在波に対応する電気信号を受信し、検波器6では、定在波が信号電圧の2乗値であるパワーp(f,xs)として検出される。
【0018】
また、パワーp(f,xs)を解析して距離スペクトルを算出する周波数解析手段として、A/Dコンバータ7及びFFT手段8が設けられており、検波器6により検出された信号のパワーp(f,xs)が、A/Dコンバータ7を経て距離スペクトル算出手段であるFFT手段8によって、距離スペクトルP(x)に変換される。本発明では特に、信号のパワーを周波数の変化分fdの関数として、つまり、p(fd,xs)とし、これを周波数解析手段のFFT手段8により周波数解析することによって、距離変数を含まない位相項を有する距離スペクトルを算出することを特徴としている。
【0019】
さらに、図示しないが前記周波数解析手段により算出された距離スペクトルの位相情報に基づき、ターゲットまでの距離を求める距離算出手段が設けられている。フーリエ変換手段8や距離算出手段は、汎用の中央演算装置(CPU)のプログラム処理によって動作する信号処理部により処理させることができる。また、このような信号処理部はデジタル信号プロセッサ(DSP)を用いて高速化させることもできる。
【0020】
本発明の特徴である上記した周波数解析手段、及びその後の距離算出手段を除いて、周波数解析手段による処理までの内容については、特許文献2として挙げた従来の距離測定装置と同様に構成することができる。
【0021】
以下、本例に係る距離測定装置の測定原理に基づいて説明する。
【0022】
信号源の振幅をA、周波数をf、光速をcとして、進行波が次式で表されるものとする。
【数1】

ただし、x軸上の任意の一点をx=0としている。k番目のターゲットの距離をdk、反射係数の大きさと位相をそれぞれγk、φkとすれば、そのターゲットからの反射波は次のように表すことができる。
【数2】

【0023】
進行波と反射波との干渉により定在波が発生するように、周波数コントローラ9で周波数fを段階的に,かつ,少なくとも信号がレーダとターゲット間を往復する時間以上の間隔をもって周波数の切り替えを行なう。このとき,送信波(進行波)と受信波(反射波)の周波数が一致するタイミングが生じ、この時点で定在波が発生する。送受信波の周波数が一致する時点において,x=xsの位置に置いた検波器6で観測される信号の電力(パワー)は、次のように表される。
【数3】

【0024】
周波数fの範囲は有限であるから、その中心をf0、幅fWとおいて、f=f0+fd、−fW/2<fd<+fW/2とする。ここで、中心周波数f0は定数であり、fdは周波数の変化分を表す変数である。通常、反射波の大きさは非常に小さくγk≪1と考えられる。以上より、p(f,xs)はfdの関数として次のように表すことができる。
【数4】

【0025】
(4)式において、
【数5】

とおけば、(4)式は次のように表すことができる。
【数6】

ここで,f0≫fdとすれば、f0+fd=f0と近似することができ,
【数7】

と表すことができる。
【0026】
(6)式の第1項は送信波(進行波)の電力、第2項は反射波の電力、第3項が定在波の発生によって生じた成分である。一般のレーダは反射波の電力γk2を受信し信号処理を行うが、本発明および特許文献1乃至3に記載の手法では第3項を用いる。第3項の振幅は2γkである。γk≪1であれば、明らかに2γk≫γk2であるので、送信電力や環境が同じ場合、一般のレーダよりもSN比のよい信号を得ることができる。これは、レーダ断面積の小さなターゲットや遠距離のターゲットに対して有効な性質である。
【0027】
ここで、X=0、X=π/2となるような2ヶ所を検出点とすれば、以下のように互いに直交する2つの信号が得られる。
X=0のとき
【数8】

(6)式に代入すると
【数9】

となる。
X=π/2のとき
【数10】

ただし、λ=c/f0である。(6)式に代入すると
【数11】

となる。
【0028】
p(fd,0)、p(fd,−λ/8)に対して、直流成分の除去のためfdで微分を行う。
【数12】

【数13】

2つの信号は直交関係にあるため、−pdiff(fd,−λ/8)を実数部、−pdiff(fd,0)を虚数部として構築される解析信号pa(fd)は、
【数14】

となる。
【0029】
図3は、距離dのところにターゲットがひとつ存在する場合に観測されるpa(fd)の実数部、および虚数部を示したものである。このようにpa(fd)は周期関数であり、その周期はターゲットとの距離に逆比例の関係にあるので、pa(fd)をフーリエ変換することによって距離dを求めることができる。
【0030】
すなわち、フーリエ変換公式
【数15】

において、ω/2πを2x/cに、tをfdに、f(t)をpa(fd)に置き換え、距離スペクトルP(x)を求める。
【数16】

ただし、
【数17】

である。これにより距離変数を含まない位相項を有する距離スペクトルが算出される。
【0031】
FFT手段8による距離スペクトルP(x)の算出において、M点FFTで求められる距離スペクトルは離散的、すなわち、x=mΔx(m=0,1,2,…,M−1)となり
、
【数18】

で与えられる。Δxは、Mと被変換データPa(fd)のデータ長Lに依存し
【数19】

で表される。
【0032】
P(mΔx)の絶対値のピーク位置がm=mpeakであれば、ターゲットの距離はmpeak
Δxで与えられる。つまり、距離の分解能はΔxである。Mを大きくすればΔxは小さく
なり分解能は高くなるが、高い分解能を得るには計算時間の増大がネックとなる場合が考えられる。しかしながら、本発明では、このMを大きくすることなく高い分解能で距離を求めることができる。
【0033】
本実施形態においては、距離算出手段により、2つの距離スペクトルの位相差からの距離を測定する。図4は、図3と同様に距離dのところにターゲットがひとつ存在する場合に観測されるpa(fd)の実部、及び虚部を示したものである。2つの異なる中心周波数f01,f02(f01<f02)に振り幅fWを与えれば、各中心周波数に対応してそれぞれ距離スペクトルが得られる。
【0034】
中心周波数がf01のときの距離スペクトルは、
【数20】

中心周波数がf02のときの距離スペクトルは
【数21】

である。距離スペクトル間の位相差をΔΨkとすると,
【数22】

で与えられる。これから,距離dkは次式で求められる。
【数23】

【0035】
ΔΨkは、0〜2πの範囲にラップされており、したがって求められる距離もある範囲
に制限される。この範囲をDとし、これを計測レンジとよぶ。Dは、ΔΨk=2πに対応
する距離であり、
【数24】

したがって、位相差ΔΨkから求められる距離の範囲は、
【数25】

である。この式からわかるように、距離測定範囲は中心周波数の差により、任意に設定することができる。もちろん、中心周波数の差の異なる複数の条件から距離を求めることも好ましい。
【0036】
次に、第2実施形態について説明する。
【0037】
本実施形態は、進行波と反射波との混合波を用いて算出する方法であり、定在波を形成させるものではない。したがって、送信波(進行波)の周波数についても、段階的に切り替える必要がなく、連続的に変化させることができる。基本構成は、上記第1実施形態と同じく図1のとおりである。
【0038】
例として、瞬時周波数fが次式、および図2で表されるリニアFM信号を送信波として用いる場合について述べる。
【数26】

【数27】

送信波を
【数28】

とすれば、反射波は次式で表すことができる。
【数29】

送信波と反射波の混合波のパワーは、
【数30】

γk≪1、fW≪f0、dk/c≪tWとすれば、送信波の周波数を段階的に切り替える場合(第1実施形態)と同じく、
【数31】

を得る。したがって、これ以降の周波数解析手段、及びその後の距離算出手段の処理については、上記第1実施形態と同様となり、その説明は省略する。
【0039】
次に、第3実施形態について説明する。
【0040】
上記第1および第2実施形態では、周波数解析手段により、複数の異なる中心周波数に基づいてそれぞれ距離スペクトルを算出し、その位相差に基づき、ターゲットまでの距離を求めたが、本実施形態ではこのような位相差を用いるのではなく、位相から距離を求めるものである。
【0041】
上記の(18)式の位相項は、真の距離dkにより一意に決まるので、位相から距離dkを求めることができる。すなわち、(18)式の位相をΨkとおけば、
【数32】

よって,
【数33】

ただし、φkは既知でなければならない。位相Ψk+φkは、0〜2πの範囲にラップされている。この位相から得られる距離は,0〜計測レンジDまでの限られた範囲の値となる。計測レンジDは、Ψk+φk=2πに対応する距離であり、この場合、
【数34】

に対応する。距離dkが計測レンジを越えた場合、(32)式は、真の距離dkとは異なるものとなる。これをdk’とすれば,真の距離dkは、
【数35】

で求めることができる。このときαは、
【数36】

である。
【数37】

は実数xに対してxを超えない最大の整数を表す。
【0042】
(34)式から明らかなように、αは連続の値をとらなければならない。よって、(35)式より、次の条件が得られる。
【数38】

つまり、Δx≦Dでなければならない。この条件を成立させるために、上記第1実施形
態に基づき(24)式により、計測レンジDを設定してもよい。
【0043】
以上、本発明の実施形態について説明したが、本発明はこうした実施例に何ら限定されるものではなく、本発明の要旨を逸脱しない範囲において種々なる形態で実施し得ることは勿論である。
【実施例】
【0044】
(シミュレーション)
以下の条件に基づき、実施例1として位相差から距離を求めた(上記第1実施形態の計算手法)。また、本手法の実施例1との比較のため、比較例1として距離スペクトルのピーク位置から距離を推定するシミュレーション(特許文献3に記載の手法)も行った。
【0045】
(実施例1の条件)
中心周波数f01=24.029GHz、f02=24.047GHz
周波数範囲fW=56.25MHz
光速c=3×108
被変換信号データ長L=192
FFT演算データ長M=256
検出位置xs=0、xs=−1.56mm
送信波の振幅A=1.0
反射係数rk=0.01,φk=π
【0046】
f01=24.029GHzを中心にfW=±28.125の振り幅をもつ。同様に、f02=24.047GHzを中心にfW=±28.125の振り幅をもつ。被変換信号のデータ長Lは192であるが、0埋めによりFFT演算データ長M=256としてFFT演算を行なう。これらの異なる2つの中心周波数に対応した距離スペクトルを算出し、その位相差を求める。
【0047】
(比較例1の条件)
中心周波数f01=24.038GHz
周波数範囲fW=75MHz
光速c=3×108
被変換信号データ長L=256
FFT演算のデータ長M=256
検出位置xs=0、xs=−1.56mm
送信波の振幅A=1.0
反射係数rk=0.01,φk=π
【0048】
(結果)
シミュレーションは、上記条件でシングルターゲット、複数ターゲットで行い、ターゲットは1mmずつ0m〜127mまで移動させた。
図5〜8はシングルターゲットでシミュレーションを行った結果であり、図5、6は実施例1により距離を算出した結果、図7、8は比較例1により距離スペクトルのピーク位置から距離を推定した結果である。図6は図5の0m〜5mの間を拡大したもの、図8は図7の0m〜5mの間を拡大したものである。
図9、10は複数ターゲットでシミュレーションを行った結果であり、図9は実施例1による結果、図10は比較例1による結果である。複数ターゲットのシミュレーションでは、それぞれのターゲット位置、推定距離、誤差を示す。
【0049】
図5、6に示すように、実施例1では、算出距離と真値がほぼ重なっている。この結果から、実施例1では、FFTのデータポイントを増やすことなくミリ単位で距離を求めることが可能であることがわかる。実施例1の場合、真値との差は0.8mm程度とごく小さい値であり、少なくとも1mmの分解能が得られることを確認することができた。実施例1では、位相差ΔΨから距離を算出するため、距離の分解能はΔΨの分解能に依存する
。つまり、理論上は位相差ΔΨの分解能に限界はない。比較例1では、真値との差は分解
能に依存しており、当然ながら分解能に相当する±1m以内で差が生じていることが確認できた。また、複数ターゲットの場合においても、実施例1は、図9に示すように高い分解能で距離を求めることが可能であり、真値との差(誤差)は数センチ以内と極めて真値(ターゲット位置)に近いことがわかる。比較例1によりFFTのピーク位置から距離を推定した場合は、図10に示すように推定距離は分解能に依存しており、真値の差(誤差)は数十センチと提案手法に比べて大きいことがわかる。
【符号の説明】
【0050】
1 距離測定装置
2 電圧制御発振器
3 伝送系
4 アンテナ
5 ターゲット
6 検波器
7 コンバータ
8 FFT手段
9 周波数コントローラ
【技術分野】
【0001】
本発明は、ターゲット(測定対象)までの距離を非接触で測定できる距離測定方法及び装置に関するものである。
【背景技術】
【0002】
この種の非接触距離測定方法としては、例えばマイクロ波、ミリ波レーダの方式としてパルス、FMCW、周波数拡散などのタイプがこれまで研究開発されてきた。特に、FMCWレーダは、比較的簡素な構成で実用的な距離測定性能が実現できることから様々な用途に使用されている。一方、これらとは別のタイプのレーダとして、送信波と受信波を分離せずその干渉により生ずる定在波を利用して距離測定を行うレーダがある(例えば、特許文献1、2参照。)。このレーダは非常に簡素な構成でありながら比較的精度のよい距離測定が可能であり、0mからの距離測定も可能となっている。更に、定在波を利用することなく送信波と受信波の混合波を解析して算出方法も提案されている(特許文献3)。
【0003】
上記特許文献1乃至3に記載の従来の手法において、距離スペクトルはフーリエ変換など周波数スペクトル解析手段によって求めるものとなっている。現実の装置においてフーリエ変換は、FFT(高速フーリエ変換)演算によって実行される。よってレーダの分解能は、距離スペクトル算出前の検出波電力値のデータサンプル数、つまり被変換データ長と、FFT演算におけるデータ長に依存するが、レベル計などの用途においては、数ミリ単位の分解能が要求される。上記特許文献1乃至3に記載の従来の手法においては、位相が距離変数xに依存し、特に特許文献1の手法においては、位相差が距離スペクトルのピーク付近で距離に対して変化し、ターゲットの距離で零となる。これにより、零クロス点を探索する手法となる。しかしながら、零クロス点を正確に探すためには距離スペクトルを細かく計算する必要があり、そのためにはFFT演算におけるデータ長を大きくする必要がある。その結果、計算量が増え、処理速度が遅くなってしまう。あるいは、高価な演算装置の使用が避けられず、コストアップになり、省電力化や装置の小型化への要求にも十分応えられない。
【0004】
高価な演算装置の使用を避け、現実的なコストや処理速度の範囲で算出するとなると、分解能を上げることができず、測定精度を出すことができない。例えば、周波数範囲fw=75MHz、被変換データ長が256点に対してFFT演算におけるデータ長が1024点の場合、分解能は0.5mとなる。同条件で1mmの分解能を得るためには、FFT演算におけるデータ長が512000点以上必要となり、上記のとおりコストアップが避けられず、このような距離測定装置を提供することは現実的には不可能であった。
【先行技術文献】
【特許文献】
【0005】
【特許文献1】国際公開第03/104841号パンフレット
【特許文献2】特開2002−357656号公報
【特許文献3】特開2007−93576号公報
【発明の概要】
【発明が解決しようとする課題】
【0006】
そこで、本発明が前述の状況に鑑み、解決しようとするところは、高い分解能で効率よく距離測定することができ、コストアップを避けることが可能となり、省電力化や装置の小型化も実現できる高分解能距離測定方法及び距離測定装置を提供する点にある。
【課題を解決するための手段】
【0007】
本発明者は、前述の課題解決のため、鋭意検討を重ねた結果、従来の手法は距離スペクトルを求めるときに位相が距離変数xに依存し、位相差が距離スペクトルのピーク付近で距離に対して変化し、このためターゲットの距離で零となる零クロス点を探索する必要があるのであり、この零クロス点を正確に探すために、FFT演算におけるデータ長を大きくし、距離スペクトルを細かく計算する必要が生じていたという点に着眼し、このような零クロス点の探索を不要とし、より高い分解能で効率よく算出できる新たな手法を見い出し、本発明を完成するに至ったものである。
【0008】
すなわち本発明は、信号源から進行波を発生させる手順と、進行波と進行波がターゲットで反射した反射波とが干渉して発生する定在波、或いは進行波と反射波との混合波を検出する手順と、当該定在波又は混合波の周波数解析により、距離スペクトルを算出する手順と、該距離スペクトルの位相情報から、ターゲットまでの距離を求める手順とを備える距離測定方法であって、前記周波数解析が、定在波又は混合波を周波数の変化分の関数としてフーリエ変換を行うことにより、距離変数を含まない位相項を有する距離スペクトルを算出してなることを特徴とする位相情報を用いた高分解能距離測定方法を提供する。
【0009】
ここで、前記周波数解析が、複数の異なる中心周波数に基づいてそれぞれ距離スペクトルを算出し、その位相差に基づき、ターゲットまでの距離を求めることが好ましい。
【0010】
また本発明は、信号源から進行波を発生させる進行波発生手段と、進行波と進行波がターゲットで反射した反射波とが干渉して発生する定在波、或いは進行波と反射波との混合波を検出する検出手段と、当該定在波又は混合波の周波数解析により、距離スペクトルを算出する周波数解析手段と、該距離スペクトルの位相情報から、ターゲットまでの距離を求める距離算出手段とを備え、前記周波数解析手段が、定在波又は混合波を周波数の変化分の関数としてフーリエ変換を行い、距離変数を含まない位相項を有する距離スペクトルを算出してなることを特徴とする位相情報を用いた高分解能距離測定装置をも提供する。
【発明の効果】
【0011】
以上にしてなる本願発明に係る高分解能距離測定方法及び装置によれば、周波数解析のときに定在波又は混合波を周波数の変化分の関数としてフーリエ変換を行うことにより、距離変数を含まない位相項を有する距離スペクトルを算出したので、算出される距離スペクトルのピーク付近の位相(位相差)が一定となり、かつ、ターゲットの距離に比例した値となることから、従来のようにFFT演算におけるデータ長を大きくし、距離スペクトルを細かく計算し、零クロス点を探索するといった処理を経ることなく、位相情報から直接、高分解能で精度よく距離が算出される。したがって、計算量も少なくて済み、算出速度が向上するので、コストアップを避け、省電力化や装置の小型化を実現することもできる。
【0012】
また、周波数解析として、複数の異なる中心周波数に基づいてそれぞれ距離スペクトルを算出し、その位相差に基づき、ターゲットまでの距離を求めたので、計測レンジを測りたい距離にあわせて距離を測定することができる。
【図面の簡単な説明】
【0013】
【図1】本発明に係る高分解能距離測定装置の構成を示す概略説明図。
【図2】第2実施形態における送信波であるリニアFM信号を示す説明図。
【図3】解析信号pa(fd)を示す説明図。
【図4】同じく解析信号pa(fd)を示す説明図。
【図5】実施例1のシングルターゲットのシミュレーション結果を示すグラフ
【図6】図5の0m〜5mの間を拡大したグラフ。
【図7】比較例1のシングルターゲットのシミュレーション結果を示すグラフ。
【図8】図7の0m〜5mの間を拡大したグラフ。
【図9】実施例1の複数ターゲットのシミュレーション結果を示す説明図。
【図10】比較例1の複数ターゲットのシミュレーション結果を示す説明図。
【発明を実施するための形態】
【0014】
次に、本発明の実施形態を添付図面に基づき詳細に説明する。
【0015】
尚、以下の説明においては、進行波と反射波が干渉してなる定在波を検出し、これに基づき距離を測定する方法を代表例(第1実施形態)として、その算出原理などについて述べるが、第2実施形態として説明するように、進行波と反射波の混合波を検出してこれに基づき距離を算出する方法も同様に採用できる。また、ターゲット5が複数の場合について説明したが、勿論一つのみの場合であっても同様である。
【0016】
本発明に係る高分解能距離測定装置1は、図1に示すように、信号源から進行波VTを発生させる進行波発生手段として、高周波の電気信号を発生する電圧制御発振器2(VOC(Voltage Controlled Oscillator))、これを電力増幅やインピーダンス整合を行う伝送系3、周波数コントローラ9、及びアンテナ4が設けられている。電圧制御発振器2の発振周波数は、周波数コントローラ9から与えられる制御電圧で変化させられる。本例では、送信波(進行波)の周波数は段階的に切り替えられる。またアンテナ4は、供給される高周波の電気信号を電磁波に変換して周囲の空間に進行波VTを送信する。
【0017】
本例では、アンテナ4から送信される電磁波の進行方向でd1,d2,…,dnの距離に、測定対象となるターゲット5,…が複数存在しており、各ターゲットに入射する進行波VTと、各ターゲットからの反射波VR1,VR2,…,VRNの干渉により定在波が生じる。進行波VTと、進行波VTがターゲット5,…で反射した反射波VR1,VR2,…,VRNとが干渉して発生する定在波を検出する検出手段として、同じくアンテナ4と検波器(Power Detector)6が設けられており、アンテナ4で定在波に対応する電気信号を受信し、検波器6では、定在波が信号電圧の2乗値であるパワーp(f,xs)として検出される。
【0018】
また、パワーp(f,xs)を解析して距離スペクトルを算出する周波数解析手段として、A/Dコンバータ7及びFFT手段8が設けられており、検波器6により検出された信号のパワーp(f,xs)が、A/Dコンバータ7を経て距離スペクトル算出手段であるFFT手段8によって、距離スペクトルP(x)に変換される。本発明では特に、信号のパワーを周波数の変化分fdの関数として、つまり、p(fd,xs)とし、これを周波数解析手段のFFT手段8により周波数解析することによって、距離変数を含まない位相項を有する距離スペクトルを算出することを特徴としている。
【0019】
さらに、図示しないが前記周波数解析手段により算出された距離スペクトルの位相情報に基づき、ターゲットまでの距離を求める距離算出手段が設けられている。フーリエ変換手段8や距離算出手段は、汎用の中央演算装置(CPU)のプログラム処理によって動作する信号処理部により処理させることができる。また、このような信号処理部はデジタル信号プロセッサ(DSP)を用いて高速化させることもできる。
【0020】
本発明の特徴である上記した周波数解析手段、及びその後の距離算出手段を除いて、周波数解析手段による処理までの内容については、特許文献2として挙げた従来の距離測定装置と同様に構成することができる。
【0021】
以下、本例に係る距離測定装置の測定原理に基づいて説明する。
【0022】
信号源の振幅をA、周波数をf、光速をcとして、進行波が次式で表されるものとする。
【数1】

ただし、x軸上の任意の一点をx=0としている。k番目のターゲットの距離をdk、反射係数の大きさと位相をそれぞれγk、φkとすれば、そのターゲットからの反射波は次のように表すことができる。
【数2】

【0023】
進行波と反射波との干渉により定在波が発生するように、周波数コントローラ9で周波数fを段階的に,かつ,少なくとも信号がレーダとターゲット間を往復する時間以上の間隔をもって周波数の切り替えを行なう。このとき,送信波(進行波)と受信波(反射波)の周波数が一致するタイミングが生じ、この時点で定在波が発生する。送受信波の周波数が一致する時点において,x=xsの位置に置いた検波器6で観測される信号の電力(パワー)は、次のように表される。
【数3】

【0024】
周波数fの範囲は有限であるから、その中心をf0、幅fWとおいて、f=f0+fd、−fW/2<fd<+fW/2とする。ここで、中心周波数f0は定数であり、fdは周波数の変化分を表す変数である。通常、反射波の大きさは非常に小さくγk≪1と考えられる。以上より、p(f,xs)はfdの関数として次のように表すことができる。
【数4】

【0025】
(4)式において、
【数5】

とおけば、(4)式は次のように表すことができる。
【数6】

ここで,f0≫fdとすれば、f0+fd=f0と近似することができ,
【数7】

と表すことができる。
【0026】
(6)式の第1項は送信波(進行波)の電力、第2項は反射波の電力、第3項が定在波の発生によって生じた成分である。一般のレーダは反射波の電力γk2を受信し信号処理を行うが、本発明および特許文献1乃至3に記載の手法では第3項を用いる。第3項の振幅は2γkである。γk≪1であれば、明らかに2γk≫γk2であるので、送信電力や環境が同じ場合、一般のレーダよりもSN比のよい信号を得ることができる。これは、レーダ断面積の小さなターゲットや遠距離のターゲットに対して有効な性質である。
【0027】
ここで、X=0、X=π/2となるような2ヶ所を検出点とすれば、以下のように互いに直交する2つの信号が得られる。
X=0のとき
【数8】

(6)式に代入すると
【数9】

となる。
X=π/2のとき
【数10】

ただし、λ=c/f0である。(6)式に代入すると
【数11】

となる。
【0028】
p(fd,0)、p(fd,−λ/8)に対して、直流成分の除去のためfdで微分を行う。
【数12】

【数13】

2つの信号は直交関係にあるため、−pdiff(fd,−λ/8)を実数部、−pdiff(fd,0)を虚数部として構築される解析信号pa(fd)は、
【数14】

となる。
【0029】
図3は、距離dのところにターゲットがひとつ存在する場合に観測されるpa(fd)の実数部、および虚数部を示したものである。このようにpa(fd)は周期関数であり、その周期はターゲットとの距離に逆比例の関係にあるので、pa(fd)をフーリエ変換することによって距離dを求めることができる。
【0030】
すなわち、フーリエ変換公式
【数15】

において、ω/2πを2x/cに、tをfdに、f(t)をpa(fd)に置き換え、距離スペクトルP(x)を求める。
【数16】

ただし、
【数17】

である。これにより距離変数を含まない位相項を有する距離スペクトルが算出される。
【0031】
FFT手段8による距離スペクトルP(x)の算出において、M点FFTで求められる距離スペクトルは離散的、すなわち、x=mΔx(m=0,1,2,…,M−1)となり
、
【数18】

で与えられる。Δxは、Mと被変換データPa(fd)のデータ長Lに依存し
【数19】

で表される。
【0032】
P(mΔx)の絶対値のピーク位置がm=mpeakであれば、ターゲットの距離はmpeak
Δxで与えられる。つまり、距離の分解能はΔxである。Mを大きくすればΔxは小さく
なり分解能は高くなるが、高い分解能を得るには計算時間の増大がネックとなる場合が考えられる。しかしながら、本発明では、このMを大きくすることなく高い分解能で距離を求めることができる。
【0033】
本実施形態においては、距離算出手段により、2つの距離スペクトルの位相差からの距離を測定する。図4は、図3と同様に距離dのところにターゲットがひとつ存在する場合に観測されるpa(fd)の実部、及び虚部を示したものである。2つの異なる中心周波数f01,f02(f01<f02)に振り幅fWを与えれば、各中心周波数に対応してそれぞれ距離スペクトルが得られる。
【0034】
中心周波数がf01のときの距離スペクトルは、
【数20】

中心周波数がf02のときの距離スペクトルは
【数21】

である。距離スペクトル間の位相差をΔΨkとすると,
【数22】

で与えられる。これから,距離dkは次式で求められる。
【数23】

【0035】
ΔΨkは、0〜2πの範囲にラップされており、したがって求められる距離もある範囲
に制限される。この範囲をDとし、これを計測レンジとよぶ。Dは、ΔΨk=2πに対応
する距離であり、
【数24】

したがって、位相差ΔΨkから求められる距離の範囲は、
【数25】

である。この式からわかるように、距離測定範囲は中心周波数の差により、任意に設定することができる。もちろん、中心周波数の差の異なる複数の条件から距離を求めることも好ましい。
【0036】
次に、第2実施形態について説明する。
【0037】
本実施形態は、進行波と反射波との混合波を用いて算出する方法であり、定在波を形成させるものではない。したがって、送信波(進行波)の周波数についても、段階的に切り替える必要がなく、連続的に変化させることができる。基本構成は、上記第1実施形態と同じく図1のとおりである。
【0038】
例として、瞬時周波数fが次式、および図2で表されるリニアFM信号を送信波として用いる場合について述べる。
【数26】

【数27】

送信波を
【数28】

とすれば、反射波は次式で表すことができる。
【数29】

送信波と反射波の混合波のパワーは、
【数30】

γk≪1、fW≪f0、dk/c≪tWとすれば、送信波の周波数を段階的に切り替える場合(第1実施形態)と同じく、
【数31】

を得る。したがって、これ以降の周波数解析手段、及びその後の距離算出手段の処理については、上記第1実施形態と同様となり、その説明は省略する。
【0039】
次に、第3実施形態について説明する。
【0040】
上記第1および第2実施形態では、周波数解析手段により、複数の異なる中心周波数に基づいてそれぞれ距離スペクトルを算出し、その位相差に基づき、ターゲットまでの距離を求めたが、本実施形態ではこのような位相差を用いるのではなく、位相から距離を求めるものである。
【0041】
上記の(18)式の位相項は、真の距離dkにより一意に決まるので、位相から距離dkを求めることができる。すなわち、(18)式の位相をΨkとおけば、
【数32】

よって,
【数33】

ただし、φkは既知でなければならない。位相Ψk+φkは、0〜2πの範囲にラップされている。この位相から得られる距離は,0〜計測レンジDまでの限られた範囲の値となる。計測レンジDは、Ψk+φk=2πに対応する距離であり、この場合、
【数34】

に対応する。距離dkが計測レンジを越えた場合、(32)式は、真の距離dkとは異なるものとなる。これをdk’とすれば,真の距離dkは、
【数35】

で求めることができる。このときαは、
【数36】

である。
【数37】

は実数xに対してxを超えない最大の整数を表す。
【0042】
(34)式から明らかなように、αは連続の値をとらなければならない。よって、(35)式より、次の条件が得られる。
【数38】

つまり、Δx≦Dでなければならない。この条件を成立させるために、上記第1実施形
態に基づき(24)式により、計測レンジDを設定してもよい。
【0043】
以上、本発明の実施形態について説明したが、本発明はこうした実施例に何ら限定されるものではなく、本発明の要旨を逸脱しない範囲において種々なる形態で実施し得ることは勿論である。
【実施例】
【0044】
(シミュレーション)
以下の条件に基づき、実施例1として位相差から距離を求めた(上記第1実施形態の計算手法)。また、本手法の実施例1との比較のため、比較例1として距離スペクトルのピーク位置から距離を推定するシミュレーション(特許文献3に記載の手法)も行った。
【0045】
(実施例1の条件)
中心周波数f01=24.029GHz、f02=24.047GHz
周波数範囲fW=56.25MHz
光速c=3×108
被変換信号データ長L=192
FFT演算データ長M=256
検出位置xs=0、xs=−1.56mm
送信波の振幅A=1.0
反射係数rk=0.01,φk=π
【0046】
f01=24.029GHzを中心にfW=±28.125の振り幅をもつ。同様に、f02=24.047GHzを中心にfW=±28.125の振り幅をもつ。被変換信号のデータ長Lは192であるが、0埋めによりFFT演算データ長M=256としてFFT演算を行なう。これらの異なる2つの中心周波数に対応した距離スペクトルを算出し、その位相差を求める。
【0047】
(比較例1の条件)
中心周波数f01=24.038GHz
周波数範囲fW=75MHz
光速c=3×108
被変換信号データ長L=256
FFT演算のデータ長M=256
検出位置xs=0、xs=−1.56mm
送信波の振幅A=1.0
反射係数rk=0.01,φk=π
【0048】
(結果)
シミュレーションは、上記条件でシングルターゲット、複数ターゲットで行い、ターゲットは1mmずつ0m〜127mまで移動させた。
図5〜8はシングルターゲットでシミュレーションを行った結果であり、図5、6は実施例1により距離を算出した結果、図7、8は比較例1により距離スペクトルのピーク位置から距離を推定した結果である。図6は図5の0m〜5mの間を拡大したもの、図8は図7の0m〜5mの間を拡大したものである。
図9、10は複数ターゲットでシミュレーションを行った結果であり、図9は実施例1による結果、図10は比較例1による結果である。複数ターゲットのシミュレーションでは、それぞれのターゲット位置、推定距離、誤差を示す。
【0049】
図5、6に示すように、実施例1では、算出距離と真値がほぼ重なっている。この結果から、実施例1では、FFTのデータポイントを増やすことなくミリ単位で距離を求めることが可能であることがわかる。実施例1の場合、真値との差は0.8mm程度とごく小さい値であり、少なくとも1mmの分解能が得られることを確認することができた。実施例1では、位相差ΔΨから距離を算出するため、距離の分解能はΔΨの分解能に依存する
。つまり、理論上は位相差ΔΨの分解能に限界はない。比較例1では、真値との差は分解
能に依存しており、当然ながら分解能に相当する±1m以内で差が生じていることが確認できた。また、複数ターゲットの場合においても、実施例1は、図9に示すように高い分解能で距離を求めることが可能であり、真値との差(誤差)は数センチ以内と極めて真値(ターゲット位置)に近いことがわかる。比較例1によりFFTのピーク位置から距離を推定した場合は、図10に示すように推定距離は分解能に依存しており、真値の差(誤差)は数十センチと提案手法に比べて大きいことがわかる。
【符号の説明】
【0050】
1 距離測定装置
2 電圧制御発振器
3 伝送系
4 アンテナ
5 ターゲット
6 検波器
7 コンバータ
8 FFT手段
9 周波数コントローラ
【特許請求の範囲】
【請求項1】
信号源から進行波を発生させる手順と、
進行波と進行波がターゲットで反射した反射波とが干渉して
発生する定在波、或いは進行波と反射波との混合波を検出する手順と、
当該定在波又は混合波の周波数解析により、距離スペクトルを算出する手順と、
該距離スペクトルの位相情報から、ターゲットまでの距離を求める手順とを備える距離測定方法であって、
前記周波数解析が、定在波又は混合波を周波数の変化分の関数としてフーリエ変換を行うことにより、距離変数を含まない位相項を有する距離スペクトルを算出してなることを特徴とする位相情報を用いた高分解能距離測定方法。
【請求項2】
前記周波数解析が、複数の異なる中心周波数に基づいてそれぞれ距離スペクトルを算出し、その位相差に基づき、ターゲットまでの距離を求める請求項1記載の高分解能距離測定方法。
【請求項3】
信号源から進行波を発生させる進行波発生手段と、
進行波と進行波がターゲットで反射した反射波とが干渉して発生する定在波、或いは進行波と反射波との混合波を検出する検出手段と、
当該定在波又は混合波の周波数解析により、距離スペクトルを算出する周波数解析手段と、
該距離スペクトルの位相情報から、ターゲットまでの距離を求める距離算出手段とを備え、
前記周波数解析手段が、定在波又は混合波を周波数の変化分の関数としてフーリエ変換を行い、距離変数を含まない位相項を有する距離スペクトルを算出してなることを特徴とする位相情報を用いた高分解能距離測定装置。
【請求項1】
信号源から進行波を発生させる手順と、
進行波と進行波がターゲットで反射した反射波とが干渉して
発生する定在波、或いは進行波と反射波との混合波を検出する手順と、
当該定在波又は混合波の周波数解析により、距離スペクトルを算出する手順と、
該距離スペクトルの位相情報から、ターゲットまでの距離を求める手順とを備える距離測定方法であって、
前記周波数解析が、定在波又は混合波を周波数の変化分の関数としてフーリエ変換を行うことにより、距離変数を含まない位相項を有する距離スペクトルを算出してなることを特徴とする位相情報を用いた高分解能距離測定方法。
【請求項2】
前記周波数解析が、複数の異なる中心周波数に基づいてそれぞれ距離スペクトルを算出し、その位相差に基づき、ターゲットまでの距離を求める請求項1記載の高分解能距離測定方法。
【請求項3】
信号源から進行波を発生させる進行波発生手段と、
進行波と進行波がターゲットで反射した反射波とが干渉して発生する定在波、或いは進行波と反射波との混合波を検出する検出手段と、
当該定在波又は混合波の周波数解析により、距離スペクトルを算出する周波数解析手段と、
該距離スペクトルの位相情報から、ターゲットまでの距離を求める距離算出手段とを備え、
前記周波数解析手段が、定在波又は混合波を周波数の変化分の関数としてフーリエ変換を行い、距離変数を含まない位相項を有する距離スペクトルを算出してなることを特徴とする位相情報を用いた高分解能距離測定装置。
【図1】


【図2】


【図3】


【図4】


【図5】


【図6】


【図7】


【図8】


【図9】


【図10】




【図2】


【図3】


【図4】


【図5】


【図6】


【図7】


【図8】


【図9】


【図10】


【公開番号】特開2010−271088(P2010−271088A)
【公開日】平成22年12月2日(2010.12.2)
【国際特許分類】
【出願番号】特願2009−121418(P2009−121418)
【出願日】平成21年5月19日(2009.5.19)
【出願人】(000173706)財団法人雑賀技術研究所 (11)
【Fターム(参考)】
【公開日】平成22年12月2日(2010.12.2)
【国際特許分類】
【出願日】平成21年5月19日(2009.5.19)
【出願人】(000173706)財団法人雑賀技術研究所 (11)
【Fターム(参考)】
[ Back to top ]

