情報処理装置、情報処理方法、及びプログラム
【課題】多次多変数多項式の係数を効率的に代入できるようにすること。
【解決手段】
多次多変数多項式の組F=(f1,…,fm)を含む公開鍵を利用した公開鍵認証方式又は電子署名方式のアルゴリズムを実行するエンティティの間で共有されている情報から所定の関数を用いて、前記多次多変数多項式の組Fを構成する各項の係数に利用する数を生成する数生成部と、前記数生成部が生成した数を、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式の係数に割り当てる割当部と、を備え、前記割当部は、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式の係数のうち、変数の組み合わせの種類が同じ項の係数をグループ化しておき、割り当て処理をグループ単位で実行する、情報処理装置が提供される。
【解決手段】
多次多変数多項式の組F=(f1,…,fm)を含む公開鍵を利用した公開鍵認証方式又は電子署名方式のアルゴリズムを実行するエンティティの間で共有されている情報から所定の関数を用いて、前記多次多変数多項式の組Fを構成する各項の係数に利用する数を生成する数生成部と、前記数生成部が生成した数を、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式の係数に割り当てる割当部と、を備え、前記割当部は、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式の係数のうち、変数の組み合わせの種類が同じ項の係数をグループ化しておき、割り当て処理をグループ単位で実行する、情報処理装置が提供される。
【発明の詳細な説明】
【技術分野】
【0001】
本技術は、情報処理装置、情報処理方法、及びプログラムに関する。
【背景技術】
【0002】
情報処理技術や通信技術の急速な発展に伴い、公文書、私文書を問わず、文書の電子化が急速に進んでいる。これに伴い、多くの個人や企業は、電子文書の安全管理に大きな関心を寄せている。こうした関心の高まりを受け、各方面で電子文書の盗聴や偽造等のタンパリング行為に対する対抗策が盛んに研究されるようになってきた。電子文書の盗聴に対しては、例えば、電子文書を暗号化することにより安全性が確保される。また、電子文書の偽造に対しては、例えば、電子署名を利用することにより安全性が確保される。但し、利用する暗号や電子署名が高いタンパリング耐性を有していなければ、十分な安全性が保証されない。
【0003】
電子署名は、電子文書の作成者を特定するために利用される。そのため、電子署名は、電子文書の作成者しか生成できないようにすべきである。仮に、悪意ある第三者が同じ電子署名を生成できてしまうと、その第三者が電子文書の作成者に成りすますことができてしまう。つまり、悪意ある第三者により電子文書が偽造されてしまう。こうした偽造を防止するため、電子署名の安全性については様々な議論が交わされてきた。現在広く利用されている電子署名方式としては、例えば、RSA署名方式やDSA署名方式などが知られている。
【0004】
RSA署名方式は、「大きな合成数に対する素因数分解の困難性(以下、素因数分解問題)」を安全性の根拠とする。また、DSA署名方式は、「離散対数問題に対する解の導出の困難性」を安全性の根拠とする。これらの根拠は、古典的なコンピュータを利用して素因数分解問題や離散対数問題を効率的に解くアルゴリズムが存在しないことに起因する。つまり、上記の困難性は、古典的なコンピュータにおける計算量的な困難性を意味する。しかしながら、量子コンピュータを用いると、素因数分解問題や離散対数問題に対する解答が効率的に算出されてしまうと言われている。
【0005】
現在利用されている電子署名方式や公開鍵認証方式の多くは、RSA署名方式やDSA署名方式と同様、素因数分解問題や離散対数問題の困難性に安全性の根拠をおいている。そのため、こうした電子署名方式や公開鍵認証方式は、量子コンピュータが実用化された場合に、その安全性が確保されないことになる。そこで、素因数分解問題や離散対数問題など、量子コンピュータにより容易に解かれてしまう問題とは異なる問題に安全性の根拠をおく新たな電子署名方式及び公開鍵認証方式の実現が求められている。量子コンピュータにより容易に解くことが難しい問題としては、例えば、多変数多項式問題がある。
【0006】
多変数多項式問題に安全性の根拠をおく電子署名方式としては、例えば、MI(Matsumoto−Imai cryptography)、HFE(Hidden Field Equation cryptography)、OV(Oil−Vinegar signature scheme)、TTM(Tamed Transformation Method cryptography)に基づく方式が知られている。例えば、下記の非特許文献1、2には、HFEに基づく電子署名方式が開示されている。
【先行技術文献】
【非特許文献】
【0007】
【非特許文献1】Jacques Patarin Asymmetric Cryptography with a Hidden Monomial. CRYPTO 1996, pp.45−60.
【非特許文献2】Patarin, J., Courtois, N., and Goubin, L. QUARTZ, 128−Bit Long Digital Signatures. In Naccache,D., Ed. Topics in Cryptology − CT−RSA 2001 (San Francisco, CA, USA, April 2001), vol. 2020 of Lecture Notes in Computer Science, Springer−Verlag., pp.282−297.
【発明の概要】
【発明が解決しようとする課題】
【0008】
上記の通り、多変数多項式問題は、量子コンピュータを用いても解くことが困難なNP困難問題と呼ばれる問題の一例である。通常、HFEなどに代表される多変数多項式問題を利用した公開鍵認証方式は、特殊なトラップドアが仕込まれた多次多変数連立方程式を利用している。例えば、x1,…,xnに関する多次多変数連立方程式F(x1,…,xn)=yと線形変換A及びBが用意され、線形変換A及びBが秘密に管理される。この場合、多次多変数連立方程式F、線形変換A及びBがトラップドアとなる。
【0009】
トラップドアF,A,Bを知っているエンティティは、x1,…,xnに関する方程式B(F(A(x1,…,xn)))=y’を解くことができる。一方、トラップドアF,A,Bを知らないエンティティは、x1,…,xnに関する方程式B(F(A(x1,…,xn)))=y’を解くことができない。この仕組みを利用することにより、多次多変数連立方程式の解答困難性を安全性の根拠とする公開鍵認証方式や電子署名方式が実現される。
【0010】
上記の通り、こうした公開鍵認証方式や電子署名方式を実現するには、B(F(A(x1,…,xn)))=yを満たすような特殊な多次多変数連立方程式を用意する必要がある。また、署名生成時に多次多変数連立方程式Fを解く必要がある。そのため、利用可能な多次多変数連立方程式Fは、比較的容易に解けるものに限られていた。すなわち、これまでの方式においては、比較的容易に解ける3つの関数(トラップドア)B、F、Aを合成した形の多次多変数連立方程式B(F(A(x1,…,xn)))=yしか用いることができず、十分な安全性を確保することが難しかった。
【0011】
そこで、本件発明者は、上記の事情に鑑みて、効率的に解く手段(トラップドア)が知られていない多次多変数連立方程式を用いて高い安全性を有する効率的な公開鍵認証方式及び電子署名方式を考案した(Koichi Sakumoto,Taizo Shirai and Harunaga Hiwatari,“Public−Key Identification Schemes Based on Multivariate Quadratic Polynomials”,CRYPTO 2011,LNCS 6841,pp.706−723,2011.)。
【0012】
しかし、この公開鍵認証方式及び電子署名方式で利用する多変数多項式は係数の数が多く、公開鍵として利用するには、証明者と検証者との間で効率的に係数を割り当てる方法を決めておく必要があった。本技術は、効率的に多変数多項式の係数を代入することが可能な、新規かつ改良された情報処理装置、情報処理方法、及びプログラムの提供を意図して考案されたものである。
【課題を解決するための手段】
【0013】
本技術のある観点によれば、多次多変数多項式の組F=(f1,…,fm)を含む公開鍵を利用した公開鍵認証方式又は電子署名方式のアルゴリズムを実行するエンティティの間で共有されている情報から所定の関数を用いて、前記多次多変数多項式の組Fを構成する各項の係数に利用する数を生成する数生成部と、前記数生成部が生成した数を、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式の係数に割り当てる割当部と、を備え、前記割当部は、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式の係数のうち、変数の組み合わせの種類が同じ項の係数をグループ化しておき、割り当て処理をグループ単位で実行する、情報処理装置が提供される。
【0014】
また、本技術の別の観点によれば、多次多変数多項式の組F=(f1,…,fm)を含む公開鍵を利用した公開鍵認証方式又は電子署名方式のアルゴリズムを実行するエンティティの間で共有されている情報から所定の関数を用いて、前記多次多変数多項式の組Fを構成する各項の係数に利用する数を生成する数生成部と、前記数生成部が生成した数を、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式の係数に割り当てる割当部と、を備え、前記割当部は、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式を2次形式で表現した場合の係数行列を行又は列毎にグループ化しておき、割り当て処理をグループ単位で実行する、情報処理装置が提供される。
【0015】
また、本技術の別の観点によれば、多次多変数多項式の組F=(f1,…,fm)を含む公開鍵を利用した公開鍵認証方式又は電子署名方式のアルゴリズムを実行するエンティティの間で共有されている情報から所定の関数を用いて前記多次多変数多項式の組Fを構成する各項の係数と同じ数だけ数を生成する数生成部と、前記証明者と前記認証者との間で予め決められた順序で前記数生成部が生成した数を、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式の係数に割り当てる割当部と、を備える、情報処理装置が提供される。
【0016】
また、本技術の別の観点によれば、多次多変数多項式の組F=(f1,…,fm)を含む公開鍵を利用した公開鍵認証方式又は電子署名方式のアルゴリズムを実行するエンティティの間で共有されている情報から所定の関数を用いて、前記多次多変数多項式の組Fを構成する各項の係数に利用する数を生成するステップと、生成した数を、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式の係数に割り当てるステップと、を含み、前記割り当てるステップでは、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式の係数のうち、変数の組み合わせの種類が同じ項の係数をグループ化しておき、割り当て処理をグループ単位で実行する、情報処理方法が提供される。
【0017】
また、本技術の別の観点によれば、多次多変数多項式の組F=(f1,…,fm)を含む公開鍵を利用した公開鍵認証方式又は電子署名方式のアルゴリズムを実行するエンティティの間で共有されている情報から所定の関数を用いて、前記多次多変数多項式の組Fを構成する各項の係数に利用する数を生成するステップと、生成した数を、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式の係数に割り当てるステップと、を含み、前記割り当てるステップでは、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式を2次形式で表現した場合の係数行列を行又は列毎にグループ化しておき、割り当て処理をグループ単位で実行する、情報処理方法が提供される。
【0018】
また、本技術の別の観点によれば、多次多変数多項式の組F=(f1,…,fm)を含む公開鍵を利用した公開鍵認証方式又は電子署名方式のアルゴリズムを実行するエンティティの間で共有されている情報から所定の関数を用いて前記多次多変数多項式の組Fを構成する各項の係数と同じ数だけ数を生成するステップと、前記証明者と前記認証者との間で予め決められた順序で前記数生成部が生成した数を、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式の係数に割り当てるステップと、を含む、情報処理方法が提供される。
【0019】
また、本技術の別の観点によれば、多次多変数多項式の組F=(f1,…,fm)を含む公開鍵を利用した公開鍵認証方式又は電子署名方式のアルゴリズムを実行するエンティティの間で共有されている情報から所定の関数を用いて、前記多次多変数多項式の組Fを構成する各項の係数に利用する数を生成する数生成機能と、前記数生成機能が生成した数を、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式の係数に割り当てる割当機能と、をコンピュータに実現させるためのプログラムであり、前記割当機能は、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式の係数のうち、変数の組み合わせの種類が同じ項の係数をグループ化しておき、割り当て処理をグループ単位で実行する、プログラムが提供される。
【0020】
また、本技術の別の観点によれば、多次多変数多項式の組F=(f1,…,fm)を含む公開鍵を利用した公開鍵認証方式又は電子署名方式のアルゴリズムを実行するエンティティの間で共有されている情報から所定の関数を用いて、前記多次多変数多項式の組Fを構成する各項の係数に利用する数を生成する数生成機能と、前記数生成機能が生成した数を、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式の係数に割り当てる割当機能と、をコンピュータに実現させるためのプログラムであり、前記割当機能は、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式を2次形式で表現した場合の係数行列を行又は列毎にグループ化しておき、割り当て処理をグループ単位で実行する、プログラムが提供される。
【0021】
また、本技術の別の観点によれば、多次多変数多項式の組F=(f1,…,fm)を含む公開鍵を利用した公開鍵認証方式又は電子署名方式のアルゴリズムを実行するエンティティの間で共有されている情報から所定の関数を用いて前記多次多変数多項式の組Fを構成する各項の係数と同じ数だけ数を生成する数生成機能と、前記証明者と前記認証者との間で予め決められた順序で前記数生成部が生成した数を、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式の係数に割り当てる割当機能と、をコンピュータに実現させるためのプログラムが提供される。
【0022】
また、本技術の別の観点によれば、上記のプログラムが記録された、コンピュータにより読み取り可能な記録媒体が提供される。
【発明の効果】
【0023】
以上説明したように本技術によれば、効率的に多変数多項式の係数を代入することが可能になる。
【図面の簡単な説明】
【0024】
【図1】公開鍵認証方式に係るアルゴリズムの構成について説明するための説明図である。
【図2】電子署名方式に係るアルゴリズムの構成について説明するための説明図である。
【図3】nパスの公開鍵認証方式に係るアルゴリズムの構成について説明するための説明図である。
【図4】3パスの公開鍵認証方式に係る効率的なアルゴリズムについて説明するための説明図である。
【図5】3パスの公開鍵認証方式に係る効率的なアルゴリズムの並列化について説明するための説明図である。
【図6】3パスの公開鍵認証方式に係る効率的なアルゴリズムについて説明するための説明図である。
【図7】5パスの公開鍵認証方式に係る効率的なアルゴリズムの構成例について説明するための説明図である。
【図8】5パスの公開鍵認証方式に係る効率的なアルゴリズムの並列化について説明するための説明図である。
【図9】5パスの公開鍵認証方式に係る効率的なアルゴリズムの並列化について説明するための説明図である。
【図10】3パスの公開鍵認証方式に係る効率的なアルゴリズムを電子署名方式のアルゴリズムに変形する方法について説明するための説明図である。
【図11】5パスの公開鍵認証方式に係る効率的なアルゴリズムを電子署名方式のアルゴリズムに変形する方法について説明するための説明図である。
【図12】ハッシュ関数の構造例について説明するための説明図である。
【図13】3パス方式に基づく電子署名方式に係る署名検証方法(通常の実装方法)について説明するための説明図である。
【図14】3パス方式に基づく電子署名方式に係る署名検証方法(メモリ削減方法)について説明するための説明図である。
【図15】5パス方式に基づく電子署名方式に係る署名検証方法(通常の実装方法)について説明するための説明図である。
【図16】5パス方式に基づく電子署名方式に係る署名検証方法(メモリ削減方法)について説明するための説明図である。
【図17】2進乱数から3進乱数を抽出する方法(抽出方法#1)について説明するための説明図である。
【図18】2進乱数から3進乱数を抽出する方法(抽出方法#2)について説明するための説明図である。
【図19】2進乱数から3進乱数を抽出する方法(抽出方法#3)について説明するための説明図である。
【図20】2進乱数から3進乱数を抽出する方法(抽出方法#3)について説明するための説明図である。
【図21】2進乱数から3進乱数を抽出する方法(抽出方法#3)について説明するための説明図である。
【図22】多変数多項式の係数を効率的に代入するためのデータ構造化手法(構造化手法#1)について説明するための説明図である。
【図23】多変数多項式の係数を効率的に代入するためのデータ構造化手法(構造化手法#1)について説明するための説明図である。
【図24】多変数多項式の係数を効率的に代入するためのデータ構造化手法(構造化手法#1)について説明するための説明図である。
【図25】多変数多項式の係数を効率的に代入するためのデータ構造化手法(構造化手法#1)について説明するための説明図である。
【図26】多変数多項式の係数を効率的に代入するためのデータ構造化手法(構造化手法#1)について説明するための説明図である。
【図27】多変数多項式の係数を効率的に代入するためのデータ構造化手法(構造化手法#2)について説明するための説明図である。
【図28】本技術の各実施形態に係るアルゴリズムを実行することが可能な情報処理装置のハードウェア構成例について説明するための説明図である。
【発明を実施するための形態】
【0025】
以下に添付図面を参照しながら、本技術の好適な実施の形態について詳細に説明する。なお、本明細書及び図面において、実質的に同一の機能構成を有する構成要素については、同一の符号を付することにより重複説明を省略する。
【0026】
[説明の流れについて]
ここで、以下に記載する本技術の実施形態に関する説明の流れについて簡単に述べる。まず、図1を参照しながら、公開鍵認証方式のアルゴリズム構成について説明する。次いで、図2を参照しながら、電子署名方式のアルゴリズム構成について説明する。次いで、図3を参照しながら、nパスの公開鍵認証方式について説明する。
【0027】
次いで、図4〜図6を参照しながら、3パスの公開鍵認証方式に係るアルゴリズムの構成例について説明する。次いで、図7〜図9を参照しながら、5パスの公開鍵認証方式に係るアルゴリズムの構成例について説明する。次いで、図10及び図11を参照しながら、3パス及び5パスの公開鍵認証方式に係る効率的なアルゴリズムを電子署名方式のアルゴリズムに変形する方法について説明する。
【0028】
次いで、図12〜図16を参照しながら、本実施形態に係る電子署名方式のアルゴリズムを実行する際に署名検証に要するメモリ量を削減する方法について説明する。次いで、図17〜図21を参照しながら、2進乱数から3進乱数を効率的に抽出する方法について説明する。次いで、図22〜図27を参照しながら、多変数多項式の係数を効率的に代入する方法について説明する。次いで、図28を参照しながら、本技術の実施形態に係る各アルゴリズムを実現することが可能な情報処理装置のハードウェア構成例について説明する。最後に、本実施形態の技術的思想について纏め、当該技術的思想から得られる作用効果について簡単に説明する。
【0029】
(説明項目)
1:はじめに
1−1:公開鍵認証方式のアルゴリズム
1−2:電子署名方式のアルゴリズム
1−3:nパスの公開鍵認証方式
2:3パスの公開鍵認証方式に係るアルゴリズムの構成
2−1:具体的なアルゴリズムの構成例
2−2:並列化アルゴリズムの構成例
2−3:3次多変数多項式に基づくアルゴリズムの構成例
3:5パスの公開鍵認証方式に係るアルゴリズムの構成
3−1:具体的なアルゴリズムの構成例
3−2:並列化アルゴリズムの構成例
3−3:3次多変数多項式に基づくアルゴリズムの構成例
4:電子署名方式への変形
4−1:3パスの公開鍵認証方式から電子署名方式への変形
4−2:5パスの公開鍵認証方式から電子署名方式への変形
5:署名検証に要するメモリ量の削減方法について
5−1:ハッシュ関数の構造について
5−2:3パス方式に基づく電子署名方式への適用例
5−3:5パス方式に基づく電子署名方式への適用例
6:2進数の乱数列から3進数の乱数列を抽出する方法について
6−1:抽出方法#1(2ビット区切り)
6−2:抽出方法#2(区切りなし)
6−3:抽出方法#3(kビット区切り)
6−3−1:基本構成
6−3−2:追加抽出方法
7:多変数多項式の係数を効率的に代入する方法について
7−1:基本的な取り決め
7−2:データの構造化
7−2−1:構造化手法#1
7−2−2:構造化手法#2
7−2−3:構造化手法#3
8:ハードウェア構成例
9:まとめ
【0030】
<1:はじめに>
本実施形態は、多次多変数連立方程式に対する求解問題の困難性に安全性の根拠をおく公開鍵認証方式及び電子署名方式に関する。但し、本実施形態は、HFE電子署名方式などの従来手法とは異なり、効率的に解く手段(トラップドア)を持たない多次多変数連立方程式を利用する公開鍵認証方式及び電子署名方式に関する。まず、公開鍵認証方式のアルゴリズム、電子署名方式のアルゴリズム、及びnパスの公開鍵認証方式について、その概要を簡単に説明する。
【0031】
[1−1:公開鍵認証方式のアルゴリズム]
まず、図1を参照しながら、公開鍵認証方式のアルゴリズムについて概要を説明する。図1は、公開鍵認証方式のアルゴリズムについて概要を説明するための説明図である。
【0032】
公開鍵認証は、ある人(証明者)が、公開鍵pk及び秘密鍵skを利用して、他の人(検証者)に本人であることを納得させるために利用される。例えば、証明者Aの公開鍵pkAは、検証者Bに公開される。一方、証明者Aの秘密鍵skAは、証明者Aにより秘密に管理される。公開鍵認証の仕組みにおいては、公開鍵pkAに対応する秘密鍵skAを知る者が証明者A本人であるとみなされる。
【0033】
公開鍵認証の仕組みを利用して証明者Aが証明者A本人であることを検証者Bに証明するには、対話プロトコルを介して、証明者Aが公開鍵pkAに対応する秘密鍵skAを知っているという証拠を検証者Bに提示すればよい。そして、証明者Aが秘密鍵skAを知っているという証拠が検証者Bに提示され、その証拠を検証者Bが確認し終えた場合、証明者Aの正当性(本人であること)が証明されたことになる。
【0034】
但し、公開鍵認証の仕組みには、安全性を担保するために以下の条件が求められる。
【0035】
1つ目の条件は、「対話プロトコルを実行した際に秘密鍵skを持たない偽証者により偽証が成立してしまう確率を限りなく小さくする」ことである。この1つ目の条件が成り立つことを「健全性」と呼ぶ。つまり、健全性とは、「秘密鍵skを持たない偽証者により、対話プロトコルの実行中に無視できない確率で偽証が成立することはないこと」と言い換えられる。2つ目の条件は、「対話プロトコルを実行したとしても、証明者Aが有する秘密鍵skAの情報が検証者Bに一切漏れることがない」ことである。この2つ目の条件が成り立つことを「零知識性」と呼ぶ。
【0036】
安全に公開鍵認証を行うには、健全性及び零知識性を有する対話プロトコルを利用する必要がある。仮に、健全性及び零知識性を有しない対話プロトコルを用いて認証処理を行った場合には、偽証された可能性及び秘密鍵の情報が漏れてしまった可能性が否定できないため、処理自体が成功裡に完了しても証明者の正当性を証明したことにはならない。従って、対話プロトコルの健全性及び零知識性を如何に保証するかが重要になる。
【0037】
(モデル)
公開鍵認証方式のモデルには、図1に示すように、証明者と検証者という2つのエンティティが存在する。証明者は、鍵生成アルゴリズムGenを用いて、証明者固有の秘密鍵skと公開鍵pkの組を生成する。次いで、証明者は、鍵生成アルゴリズムGenを用いて生成した秘密鍵skと公開鍵pkの組を利用して検証者と対話プロトコルを実行する。このとき、証明者は、証明者アルゴリズムPを利用して対話プロトコルを実行する。上記の通り、証明者は、証明者アルゴリズムPを利用し、対話プロトコルの中で秘密鍵skを保有している証拠を検証者に提示する。
【0038】
一方、検証者は、検証者アルゴリズムVを利用して対話プロトコルを実行し、証明者が公開している公開鍵に対応する秘密鍵を、その証明者が保有しているか否かを検証する。つまり、検証者は、証明者が公開鍵に対応する秘密鍵を保有しているか否かを検証するエンティティである。このように、公開鍵認証方式のモデルは、証明者と検証者という2つのエンティティ、及び、鍵生成アルゴリズムGen、証明者アルゴリズムP、検証者アルゴリズムVという3つのアルゴリズムにより構成される。
【0039】
なお、以下の説明において、「証明者」「検証者」という表現を用いるが、これらの表現はあくまでもエンティティを意味するものである。従って、鍵生成アルゴリズムGen、証明者アルゴリズムPを実行する主体は、「証明者」のエンティティに対応する情報処理装置である。同様に、検証者アルゴリズムVを実行する主体は、情報処理装置である。これら情報処理装置のハードウェア構成は、例えば、図28に示した通りである。つまり、鍵生成アルゴリズムGen、証明者アルゴリズムP、検証者アルゴリズムVは、ROM904、RAM906、記憶部920、リムーバブル記録媒体928などに記録されたプログラムに基づいてCPU902などにより実行される。
【0040】
(鍵生成アルゴリズムGen)
鍵生成アルゴリズムGenは、証明者により利用される。鍵生成アルゴリズムGenは、証明者に固有の秘密鍵skと公開鍵pkとの組を生成するアルゴリズムである。鍵生成アルゴリズムGenにより生成された公開鍵pkは公開される。そして、公開された公開鍵pkは、検証者により利用される。一方、鍵生成アルゴリズムGenにより生成された秘密鍵skは、証明者が秘密に管理する。そして、証明者により秘密に管理される秘密鍵skは、公開鍵pkに対応する秘密鍵skを証明者が保有していることを検証者に対して証明するために利用される。形式的に、鍵生成アルゴリズムGenは、セキュリティパラメータ1λ(λは0以上の整数)を入力とし、秘密鍵skと公開鍵pkを出力するアルゴリズムとして、下記の式(1)のように表現される。
【0041】
【数1】

【0042】
(証明者アルゴリズムP)
証明者アルゴリズムPは、証明者により利用される。証明者アルゴリズムPは、公開鍵pkに対応する秘密鍵skを証明者が保有していることを検証者に対して証明するためのアルゴリズムである。つまり、証明者アルゴリズムPは、秘密鍵skと公開鍵pkとを入力とし、対話プロトコルを実行するアルゴリズムである。
【0043】
(検証者アルゴリズムV)
検証者アルゴリズムVは、検証者により利用される。検証者アルゴリズムVは、対話プロトコルの中で、公開鍵pkに対応する秘密鍵skを証明者が保有しているか否かを検証するアルゴリズムである。検証者アルゴリズムVは、公開鍵pkを入力とし、対話プロトコルの実行結果に応じて0又は1(1bit)を出力するアルゴリズムである。なお、検証者は、検証者アルゴリズムVが0を出力した場合には証明者が不正なものであると判断し、1を出力した場合には証明者が正当なものであると判断する。形式的に、検証者アルゴリズムVは、下記の式(2)のように表現される。
【0044】
【数2】

【0045】
上記の通り、意味のある公開鍵認証を実現するには、対話プロトコルが健全性及び零知識性という2つの条件を満たしている必要がある。しかし、証明者が秘密鍵skを保有していることを証明するためには、証明者が秘密鍵skに依存した手続きを実行し、その結果を検証者に通知した上で、その通知内容に基づく検証を検証者に実行させる必要がある。秘密鍵skに依存した手続きを実行するのは、健全性を担保するために必要である。一方で、秘密鍵skの情報が一切検証者に漏れないようにする必要がある。そのため、これらの要件を満たすように、上記の鍵生成アルゴリズムGen、証明者アルゴリズムP、検証者アルゴリズムVを巧妙に設計する必要がある。
【0046】
以上、公開鍵認証方式のアルゴリズムについて、その概要を説明した。
【0047】
[1−2:電子署名方式のアルゴリズム]
次に、図2を参照しながら、電子署名方式のアルゴリズムについて概要を説明する。図2は、電子署名方式のアルゴリズムについて概要を説明するための説明図である。
【0048】
紙文書とは異なり、ある電子化されたデータに対して押印したり署名を記載したりすることはできない。そのため、電子化されたデータの作成者を証明するためには、紙文書に押印したり署名を記載したりするのと同等の効果が得られる電子的な仕組みを必要とする。この仕組みが電子署名である。電子署名とは、データの作成者しか知らない署名データをデータに関連付けて受領者に提供し、その署名データを受領者側で検証する仕組みのことを言う。
【0049】
(モデル)
電子署名方式のモデルには、図2に示すように、署名者及び検証者という2つのエンティティが存在する。そして、電子署名方式のモデルは、鍵生成アルゴリズムGen、署名生成アルゴリズムSig、署名検証アルゴリズムVerという3つのアルゴリズムにより構成される。
【0050】
署名者は、鍵生成アルゴリズムGenを利用して署名者固有の署名鍵skと検証鍵pkとの組を生成する。また、署名者は、署名生成アルゴリズムSigを利用して文書Mに付与する電子署名σを生成する。つまり、署名者は、文書Mに電子署名を付与するエンティティである。一方、検証者は、署名検証アルゴリズムVerを利用して文書Mに付与された電子署名σを検証する。つまり、検証者は、文書Mの作成者が署名者であるか否かを確認するために、電子署名σを検証するエンティティである。
【0051】
なお、以下の説明において、「署名者」「検証者」という表現を用いるが、これらの表現はあくまでもエンティティを意味するものである。従って、鍵生成アルゴリズムGen、署名生成アルゴリズムSigを実行する主体は、「署名者」のエンティティに対応する情報処理装置である。同様に、署名検証アルゴリズムVerを実行する主体は、情報処理装置である。これら情報処理装置のハードウェア構成は、例えば、図28に示した通りである。つまり、鍵生成アルゴリズムGen、署名生成アルゴリズムSig、署名検証アルゴリズムVerは、ROM904、RAM906、記憶部920、リムーバブル記録媒体928などに記録されたプログラムに基づいてCPU902などにより実行される。
【0052】
(鍵生成アルゴリズムGen)
鍵生成アルゴリズムGenは、署名者により利用される。鍵生成アルゴリズムGenは、署名者固有の署名鍵skと検証鍵pkとの組を生成するアルゴリズムである。鍵生成アルゴリズムGenにより生成された検証鍵pkは公開される。一方、鍵生成アルゴリズムGenにより生成された署名鍵skは、署名者により秘密に管理される。そして、署名鍵skは、文書Mに付与される電子署名σの生成に利用される。例えば、鍵生成アルゴリズムGenは、セキュリティパラメータ1λ(λは0以上の整数)を入力とし、署名鍵sk及び公開鍵pkを出力する。この場合、鍵生成アルゴリズムGenは、形式的に、下記の式(3)のように表現することができる。
【0053】
【数3】

【0054】
(署名生成アルゴリズムSig)
署名生成アルゴリズムSigは、署名者により利用される。署名生成アルゴリズムSigは、文書Mに付与される電子署名σを生成するアルゴリズムである。署名生成アルゴリズムSigは、署名鍵skと文書Mとを入力とし、電子署名σを出力するアルゴリズムである。この署名生成アルゴリズムSigは、形式的に、下記の式(4)のように表現することができる。
【0055】
【数4】

【0056】
(署名検証アルゴリズムVer)
署名検証アルゴリズムVerは、検証者により利用される。署名検証アルゴリズムVerは、電子署名σが文書Mに対する正当な電子署名であるか否かを検証するアルゴリズムである。署名検証アルゴリズムVerは、署名者の検証鍵pk、文書M、電子署名σを入力とし、0又は1(1bit)を出力するアルゴリズムである。この署名検証アルゴリズムVerは、形式的に、下記の式(5)のように表現することができる。なお、検証者は、署名検証アルゴリズムVerが0を出力した場合(公開鍵pkが文書Mと電子署名σを拒否する場合)に電子署名σが不当であると判断し、1を出力した場合(公開鍵pkが文書Mと電子署名σを受理する場合)に電子署名σが正当であると判断する。
【0057】
【数5】

【0058】
以上、電子署名方式のアルゴリズムについて、その概要を説明した。
【0059】
[1−3:nパスの公開鍵認証方式]
次に、図3を参照しながら、nパスの公開鍵認証方式について説明する。図3は、nパスの公開鍵認証方式について説明するための説明図である。
【0060】
上記の通り、公開鍵認証方式は、対話プロトコルの中で、証明者が公開鍵pkに対応する秘密鍵skを保有していることを検証者に証明する認証方式である。また、対話プロトコルは、健全性及び零知識性という2つの条件を満たす必要がある。そのため、対話プロトコルの中では、図3に示すように、証明者及び検証者の双方がそれぞれ処理を実行しながらn回の情報交換を行う。
【0061】
nパスの公開鍵認証方式の場合、証明者アルゴリズムPを用いて証明者により処理(工程#1)が実行され、情報T1が検証者に送信される。次いで、検証者アルゴリズムVを用いて検証者により処理(工程#2)が実行され、情報T2が証明者に送信される。さらに、k=3〜nについて処理の実行及び情報Tkの送信が順次行われ、最後に処理(工程#n+1)が実行される。このように、情報がn回送受信される方式のことを「nパス」の公開鍵認証方式と呼ぶ。
【0062】
以上、nパスの公開鍵認証方式について説明した。
【0063】
<2:3パスの公開鍵認証方式に係るアルゴリズムの構成>
以下、3パスの公開鍵認証方式に係るアルゴリズムについて説明する。なお、以下の説明において、3パスの公開鍵認証方式のことを「3パス方式」と呼ぶ場合がある。
【0064】
[2−1:具体的なアルゴリズムの構成例(図4)]
まず、図4を参照しながら、3パス方式に係る具体的なアルゴリズムの構成例について紹介する。図4は、3パス方式に係る具体的なアルゴリズムの構成について説明するための説明図である。ここでは、公開鍵pkの一部として2次多項式の組(f1(x),…,fm(x))を利用する場合について考える。但し、2次多項式fi(x)は、下記の式(6)のように表現されるものとする。また、ベクトル(x1,…,xn)をxと表記し、2次多項式の組(f1(x),…,fm(x))を多変数多項式F(x)と表記することにする。
【0065】
【数6】

【0066】
また、2次多項式の組(f1(x),…,fm(x))は、下記の式(7)のように表現することができる。また、A1,…,Amは、n×n行列である。さらに、b1,…,bmはそれぞれn×1ベクトルである。
【0067】
【数7】

【0068】
この表現を用いると、多変数多項式Fは、下記の式(8)及び式(9)のように表現することができる。この表現が成り立つことは、下記の式(10)から容易に確認することができる。
【0069】
【数8】

【0070】
このようにF(x+y)をxに依存する第1の部分と、yに依存する第2の部分と、x及びyの両方に依存する第3の部分とに分けたとき、第3の部分に対応する項G(x,y)は、x及びyについて双線形になる。以下、項G(x,y)を双線形項と呼ぶ場合がある。この性質を利用すると、効率的なアルゴリズムを構築することが可能になる。
【0071】
例えば、ベクトルt0∈Kn、e0∈Kmを用いて、多変数多項式F(x+r)のマスクに利用する多変数多項式F1(x)をF1(x)=G(x,t0)+e0と表現する。この場合、多変数多項式F(x+r0)とG(x)との和は、下記の式(11)のように表現される。ここで、t1=r0+t0、e1=F(r0)+e0とおけば、多変数多項式F2(x)=F(x+r0)+F1(x)は、ベクトルt1∈Kn、e1∈Kmにより表現することができる。そのため、F1(x)=G(x,t0)+e0に設定すれば、Kn上のベクトル及びKm上のベクトルを用いてF1及びF2を表現できるようになり、通信に必要なデータサイズの少ない効率的なアルゴリズムを実現することが可能になる。
【0072】
【数9】

【0073】
なお、F2(或いはF1)からr0に関する情報が一切漏れることはない。例えば、e1及びt1(或いはe0及びt0)を与えられても、e0及びt0(或いはe1及びt1)を知らない限り、r0の情報を一切知ることはできない。従って、零知識性が担保される。以下、上記の論理に基づいて構築された3パス方式のアルゴリズムについて説明する。ここで説明する3パス方式のアルゴリズムは、以下のような鍵生成アルゴリズムGen、証明者アルゴリズムP、検証者アルゴリズムVにより構成される。
【0074】
(鍵生成アルゴリズムGen)
鍵生成アルゴリズムGenは、環K上で定義されるm本の多変数多項式f1(x1,…,xn),…,fm(x1,…,xn)、及びベクトルs=(s1,…,sn)∈Knを生成する。次に、鍵生成アルゴリズムGenは、y=(y1,…,ym)←(f1(s),…,fm(s))を計算する。そして、鍵生成アルゴリズムGenは、(f1(x1,…,xn),…,fm(x1,…,xn),y)を公開鍵pkに設定し、sを秘密鍵に設定する。
【0075】
(証明者アルゴリズムP、検証者アルゴリズムV)
以下、図4を参照しながら、対話プロトコルの中で証明者アルゴリズムPが実行する処理及び検証者アルゴリズムVが実行する処理について説明する。この対話プロトコルの中で、証明者は、秘密鍵sの情報を検証者に一切漏らさずに、「自身がy=F(s)を満たすsを知っていること」を検証者に示す。一方、検証者は、証明者がy=F(s)を満たすsを知っているか否かを検証する。なお、公開鍵pkは、検証者に公開されているものとする。また、秘密鍵sは、証明者により秘密に管理されているものとする。以下、図4に示したフローチャートに沿って説明を進める。
【0076】
工程#1:
図4に示すように、まず、証明者アルゴリズムPは、ランダムにベクトルr0,t0∈Kn及びe0∈Kmを生成する。次いで、証明者アルゴリズムPは、r1←s−r0を計算する。この計算は、秘密鍵sをベクトルr0によりマスクする操作に相当する。さらに、証明者アルゴリズムPは、t1←r0−t0を計算する。次いで、証明者アルゴリズムPは、e1←F(r0)−e0を計算する。
【0077】
工程#1(続き):
次いで、証明者アルゴリズムPは、c0←H(r1,G(t0,r1)+e0)を計算する。次いで、証明者アルゴリズムPは、c1←H(t0,e0)を計算する。次いで、証明者アルゴリズムPは、c2←H(t1,e1)を計算する。工程#1で生成されたメッセージ(c0,c1,c2)は、検証者アルゴリズムVに送られる。
【0078】
工程#2:
メッセージ(c0,c1,c2)を受け取った検証者アルゴリズムVは、3つの検証パターンのうち、どの検証パターンを利用するかを選択する。例えば、検証者アルゴリズムVは、検証パターンの種類を表す3つの数値{0,1,2}の中から1つの数値を選択し、選択した数値を要求Chに設定する。この要求Chは証明者アルゴリズムPに送られる。
【0079】
工程#3:
要求Chを受け取った証明者アルゴリズムPは、受け取った要求Chに応じて検証者アルゴリズムVに送る返答Rspを生成する。Ch=0の場合、証明者アルゴリズムPは、返答Rsp=(r0,t1,e1)を生成する。Ch=1の場合、証明者アルゴリズムPは、返答Rsp=(r1,t0,e0)を生成する。Ch=2の場合、証明者アルゴリズムPは、返答Rsp=(r1,t1,e1)を生成する。工程#3で生成された返答Rspは、検証者アルゴリズムVに送られる。
【0080】
工程#4:
返答Rspを受け取った検証者アルゴリズムVは、受け取った返答Rspを利用して以下の検証処理を実行する。
【0081】
Ch=0の場合、検証者アルゴリズムVは、c1=H(r0−t1,F(r0)−e1)の等号が成り立つか否かを検証する。さらに、検証者アルゴリズムVは、c2=H(t1,e1)の等号が成り立つか否かを検証する。検証者アルゴリズムVは、これらの検証が全て成功した場合に認証成功を示す値1を出力し、検証に失敗があった場合に認証失敗を示す値0を出力する。
【0082】
Ch=1の場合、検証者アルゴリズムVは、c0=H(r1,G(t0,r1)+e0)の等号が成り立つか否かを検証する。さらに、検証者アルゴリズムVは、c1=H(t0,e0)の等号が成り立つか否かを検証する。検証者アルゴリズムVは、これらの検証が全て成功した場合に認証成功を示す値1を出力し、検証に失敗があった場合に認証失敗を示す値0を出力する。
【0083】
Ch=2の場合、検証者アルゴリズムVは、c0=H(r1,y−F(r1)−G(t1,r1)−e1)の等号が成り立つか否かを検証する。さらに、検証者アルゴリズムVは、c2=H(t1,e1)の等号が成り立つか否かを検証する。検証者アルゴリズムVは、これらの検証が全て成功した場合に認証成功を示す値1を出力し、検証に失敗があった場合に認証失敗を示す値0を出力する。
【0084】
以上、3パス方式に係る効率的なアルゴリズムの構成例について説明した。
【0085】
[2−2:並列化アルゴリズムの構成例(図5)]
次に、図5を参照しながら、図4に示した3パス方式のアルゴリズムを並列化する方法について説明する。なお、鍵生成アルゴリズムGenの構成については説明を省略する。
【0086】
さて、上記の対話プロトコルを適用すれば、偽証が成功する確率を2/3以下に抑制することができる。従って、この対話プロトコルを2回実行すれば、偽証が成功する確率を(2/3)2以下に抑制することができる。さらに、この対話プロトコルをN回実行すると、偽証が成功する確率は(2/3)Nとなり、Nを十分に大きい数(例えば、N=140)にすれば、偽証が成功する確率は無視できる程度に小さくなる。
【0087】
対話プロトコルを複数回実行する方法としては、例えば、メッセージ、要求、返答のやり取りを逐次的に複数回繰り返す直列的な方法と、1回分のやり取りで複数回分のメッセージ、要求、返答のやり取りを行う並列的な方法とが考えられる。さらに、直列的な方法と並列的な方法とを組み合わせたハイブリッド型の方法も考えられる。ここでは、図5を参照しながら、3パス方式に係る上記の対話プロトコルを並列的に実行するアルゴリズム(以下、並列化アルゴリズム)について説明する。
【0088】
工程#1:
図5に示すように、まず、証明者アルゴリズムPは、i=1〜Nについて以下の処理(1)〜処理(6)を実行する。
処理(1):証明者アルゴリズムPは、ランダムにベクトルr0i,t0i∈Kn及びe0i∈Kmを生成する。
処理(2):証明者アルゴリズムPは、r1i←s−r0iを計算する。この計算は、秘密鍵sをベクトルr0iによりマスクする操作に相当する。さらに、証明者アルゴリズムPは、t1i←r0i+t0iを計算する。
処理(3):証明者アルゴリズムPは、e1i←F(r0i)−e0iを計算する。
処理(4):証明者アルゴリズムPは、c0i←H(r1i,G(r1i,t0i)+e0i)を計算する。
処理(5):証明者アルゴリズムPは、c1i←H(t0i,e0i)を計算する。
処理(6):証明者アルゴリズムPは、c2i←H(t1i,e1i)を計算する。
【0089】
工程#1(続き)
i=1〜Nについて上記の処理(1)〜処理(6)を実行した後、証明者アルゴリズムPは、Cmt←H(c01,c11,c21,…,c0N,c1N,c2N)を計算する。工程#1で生成されたハッシュ値Cmtは、検証者アルゴリズムVに送られる。このように、メッセージ(c01,c11,c21,…,c0N,c1N,c2N)をハッシュ値に変換してから検証者アルゴリズムVに送ることで、通信量を削減することが可能になる。
【0090】
工程#2:
ハッシュ値Cmtを受け取った検証者アルゴリズムVは、i=1〜Nのそれぞれについて、3つの検証パターンのうち、どの検証パターンを利用するかを選択する。例えば、検証者アルゴリズムVは、i=1〜Nのそれぞれについて、検証パターンの種類を表す3つの数値{0,1,2}の中から1つの数値を選択し、選択した数値を要求Chiに設定する。要求Ch1,…,ChNは、証明者アルゴリズムPに送られる。
【0091】
工程#3:
要求Ch1,…,ChNを受け取った証明者アルゴリズムPは、受け取った要求Ch1,…,ChNのそれぞれ応じて検証者アルゴリズムVに送る返答Rsp1,…,RspNを生成する。Chi=0の場合、証明者アルゴリズムPは、Rspi=(r0i,t1i,e1i,c0i)を生成する。Chi=1の場合、証明者アルゴリズムPは、Rspi=(r1i,t0i,e0i,c2i)を生成する。Chi=2の場合、証明者アルゴリズムPは、Rspi=(r1i,t1i,e1i,c1i)を生成する。
【0092】
工程#3で生成された返答Rsp1,…,RspNは、検証者アルゴリズムVに送られる。
【0093】
工程#4:
返答Rsp1,…,RspNを受け取った検証者アルゴリズムVは、受け取った返答Rsp1,…,RspNを利用して以下の処理(1)〜処理(3)をi=1〜Nについて実行する。但し、検証者アルゴリズムVは、Chi=0の場合に処理(1)を実行し、Chi=1の場合に処理(2)を実行し、Chi=2の場合に処理(3)を実行する。
【0094】
処理(1):Chi=0の場合、検証者アルゴリズムVは、Rspiから(r0i,t1i,e1i,c0i)を取り出す。次いで、検証者アルゴリズムVは、c1i=H(r0i−t1i,F(r0i)−e1i)を計算する。さらに、検証者アルゴリズムVは、c2i=H(t1i,e1i)を計算する。そして、検証者アルゴリズムVは、(c0i,c1i,c2i)を保持する。
【0095】
処理(2):Chi=1の場合、検証者アルゴリズムVは、Rspiから(r1i,t0i,e0i,c2i)を取り出す。次いで、検証者アルゴリズムVは、c0i=H(r1i,G(t0i,r1i)+e0i)を計算する。さらに、検証者アルゴリズムVは、c1i=H(t0i,e0i)を計算する。そして、検証者アルゴリズムVは、(c0i,c1i,c2i)を保持する。
【0096】
処理(3):Chi=2の場合、検証者アルゴリズムVは、Rspiから(r1i,t1i,e1i,c1i)を取り出す。次いで、検証者アルゴリズムVは、c0i=H(r1i,y−F(r1i)−G(t1i,r1i)−e1i)を計算する。さらに、検証者アルゴリズムVは、c2i=H(t1i,e1i)を計算する。そして、検証者アルゴリズムVは、(c0i,c1i,c2i)を保持する。
【0097】
処理(1)〜処理(3)をi=1〜Nについて実行した後、検証者アルゴリズムVは、Cmt=H(c01,c11,c21,…,c0N,c1N,c2N)の等号が成り立つか否かを検証する。検証者アルゴリズムVは、この検証が成功した場合に認証成功を示す値1を出力し、検証に失敗した場合に認証失敗を示す値0を出力する。
【0098】
以上、3パス方式に係る効率的な並列化アルゴリズムの構成例について説明した。
【0099】
[2−3:3次多変数多項式に基づくアルゴリズムの構成例]
次に、下記の式(12)で表現される環R上の3次多項式flを利用した効率的なアルゴリズムの構築方法について検討してみたい。3次多項式flの組で表現される多変数多項式F=(f1,…,fm)は、下記の式(13)の関係を満たす。但し、Gx(x,y)は、xに関して1次となる項を表す。また、Gy(x,y)は、yに関して1次となる項を表す。Gx=(gx1,…,gxm)、Gy=(gy1,…,gym)と表現すると、gxl及びgylは、それぞれ下記の式(14)及び式(15)のように展開することができる。但し、gxlの右辺第2項は、x及びyのいずれに関しても1次であるため、gylに含めてもよい。
【0100】
【数10】

【0101】
上記の式(14)及び式(15)から分かるように、Gx(x,y)及びGy(x,y)は、x及びyについて加法準同型になっている。そこで、これらの性質を利用し、2次多項式fiを利用した効率的なアルゴリズムの構築方法と同様に、新たな変数r0,r1,t0,u0,e0を導入して公開鍵F(s)を分割する。
【0102】
多項式Gx,Gyが加法準同型であるから、変数r0,r1,t0,u0,e0を用いて、下記の式(16)〜式(19)の関係が成り立つ。下記の式(16)〜式(19)は、(r0,t0,u0,e0)で再現可能な第1の部分と、(r0,u1,e1)で再現可能な第2の部分と、(r1,t0,e0)で再現可能な第3の部分と、(r1,t1,u1,e1)で再現可能な第4の部分と、に分けることができる。
【0103】
例えば、下記の式(17)に含まれる「r0,t0」、下記の式(18)に含まれる「u0」、下記の式(19)に含まれる「F(r0),Gy(r0,u0),e0」、は、第1の部分である。また、下記の式(19)に含まれる「Gy(r0,u1),e1」は、第2の部分である。さらに、下記の式(16)に含まれる「e0,Gx(r0,r1)」は、第3の部分である。そして、下記の式(16)に含まれる「e1,F(r1),Gx(t1,r1)」、下記の式(17)に含まれる「t1」、下記の式(18)に含まれる「u1」は、第4の部分である。
【0104】
言い換えると、下記の式(16)は第3及び第4の部分で構成され、下記の式(17)及び下記の式(18)は第1及び第4の部分で構成され、下記の式(19)は第1及び第2の部分で構成されている。このように、下記の式(16)〜式(19)は、それぞれ2種類の部分で構成されている。
【0105】
また、秘密鍵sの定義及び下記の式(16)〜式(19)の関係から、(r0,t0,u0,e0)、(r0,u1,e1)、(r1,t0,e0)、(r1,t1,u1,e1)のいずれか1つを用いても秘密鍵sは得られないことが保証される。これらの性質を利用すると、例えば、環R上の3次多項式flを利用した効率的なアルゴリズム(以下、拡張アルゴリズム)を構築することができる。
【0106】
【数11】

【0107】
以下、具体的な拡張アルゴリズムの構成例について説明する。拡張アルゴリズムの設計に関する基本的なポイントは、下記の式(20)〜式(22)で表現されるメッセージを検証者に送ること、及び第1〜第4の部分のいずれかに関する検証を行うことの2点である。但し、この検証だけでは、第3の部分に含まれる「r1」と第4の部分に含まれる「r1」とが等しいかを検証することができない。同様に、第1の部分に含まれる「r0」と第2の部分に含まれる「r0」とが等しいか、第1の部分に含まれる「t0,e0」と第3の部分に含まれる「t0,e0」とが等しいかも検証することができない。さらに、第2の部分に含まれる「u1,e1」と第4の部分に含まれる「u1,e1」とが等しいかも検証することができない。そこで、以下では、これらの検証も可能にした構成例を紹介する。
【0108】
【数12】

【0109】
以下、図6を参照しながら、3パス方式に係る拡張アルゴリズムの構成例について説明する。なお、鍵生成アルゴリズムGenの構成については説明を省略する。
【0110】
工程#1:
図6に示すように、証明者アルゴリズムPは、ランダムにベクトルr0,t0,u0∈Kn及びe0∈Kmを生成する。次いで、証明者アルゴリズムPは、r1←s−r0を計算する。この計算は、秘密鍵sをベクトルr0によりマスクする操作に相当する。次いで、証明者アルゴリズムPは、t1←r0−t0を計算する。次いで、証明者アルゴリズムPは、u1←r1−u0を計算する。次いで、証明者アルゴリズムPは、e1←F(r0)−e0を計算する。
【0111】
工程#1(続き):
次いで、証明者アルゴリズムPは、c0←H(r1,Gx(t0,r1)+e0)を計算する。次いで、証明者アルゴリズムPは、c1←H(r0−t0,u0)を計算する。次いで、証明者アルゴリズムPは、c2←H(r0,e1−Gy(r0,u1))を計算する。次いで、証明者アルゴリズムPは、c3←H(t0,e0)を計算する。次いで、証明者アルゴリズムPは、c4←H(u1,e1)を計算する。工程#1で生成されたメッセージ(c0,c1,c2,c3,c4)は、検証者アルゴリズムVに送られる。
【0112】
工程#2:
メッセージ(c0,c1,c2,c3,c4)を受け取った検証者アルゴリズムVは、4つの検証パターンのうち、どの検証パターンを利用するかを選択する。例えば、検証者アルゴリズムVは、検証パターンの種類を表す4つの数値{0,1,2,3}の中から1つの数値を選択し、選択した数値を要求Chに設定する。この要求Chは証明者アルゴリズムPに送られる。
【0113】
工程#3:
要求Chを受け取った証明者アルゴリズムPは、受け取った要求Chに応じて検証者アルゴリズムVに送る返答Rspを生成する。Ch=0の場合、証明者アルゴリズムPは、返答Rsp=(r0,t0,u0,e0)を生成する。Ch=1の場合、証明者アルゴリズムPは、返答Rsp=(r0,u1,e1)を生成する。Ch=2の場合、証明者アルゴリズムPは、返答Rsp=(r1,t0,e0)を生成する。Ch=3の場合、証明者アルゴリズムPは、返答Rsp=(r1,t1,u1,e1)を生成する。工程#3で生成された返答Rspは、検証者アルゴリズムVに送られる。
【0114】
工程#4:
返答Rspを受け取った検証者アルゴリズムVは、受け取った返答Rspを利用して以下の検証処理を実行する。
【0115】
Ch=0の場合、検証者アルゴリズムVは、c1=H(r0−t0,u0)の等号が成り立つか否かを検証する。次いで、検証者アルゴリズムVは、c2=H(r0,F(r0)+Gy(r0,u0)−e0)の等号が成り立つか否かを検証する。次いで、検証者アルゴリズムVは、c3=H(t0,e0)の等号が成り立つか否かを検証する。検証者アルゴリズムVは、これらの検証が全て成功した場合に認証成功を示す値1を出力し、検証に失敗があった場合に認証失敗を示す値0を出力する。
【0116】
Ch=1の場合、検証者アルゴリズムVは、c2=H(r0,e1−Gy(r0,u1))の等号が成り立つか否かを検証する。次いで、検証者アルゴリズムVは、c4=H(u1,e1)の等号が成り立つか否かを検証する。検証者アルゴリズムVは、これらの検証が全て成功した場合に認証成功を示す値1を出力し、検証に失敗があった場合に認証失敗を示す値0を出力する。
【0117】
Ch=2の場合、検証者アルゴリズムVは、c0=H(r1,e0+Gx(t0,r1))の等号が成り立つか否かを検証する。次いで、検証者アルゴリズムVは、c3=H(t0,e0)の等号が成り立つか否かを検証する。検証者アルゴリズムVは、これらの検証が全て成功した場合に認証成功を示す値1を出力し、検証に失敗があった場合に認証失敗を示す値0を出力する。
【0118】
Ch=3の場合、検証者アルゴリズムVは、c0=H(r1,y−F(r1)−e1−Gx(t1,r1))の等号が成り立つか否かを検証する。次いで、検証者アルゴリズムVは、c1=H(t1,r1−u1)の等号が成り立つか否かを検証する。次いで、検証者アルゴリズムVは、c4=H(u1,e1)の等号が成り立つか否かを検証する。検証者アルゴリズムVは、これらの検証が全て成功した場合に認証成功を示す値1を出力し、検証に失敗があった場合に認証失敗を示す値0を出力する。
【0119】
以上、3パス方式に係る拡張アルゴリズムの構成例について説明した。3次多項式を利用していることにより、より高い安全性が実現されている。
【0120】
<3:5パスの公開鍵認証方式に係るアルゴリズムの構成>
次に、5パスの公開鍵認証方式に係るアルゴリズムについて説明する。なお、以下の説明において、5パスの公開鍵認証方式のことを「5パス方式」と呼ぶ場合がある。
【0121】
3パス方式の場合には対話プロトコル1回当たりの偽証確率が2/3であったが、5パス方式の場合には対話プロトコル1回当たりの偽証確率が1/2+1/qとなる。但し、qは、利用する環の位数である。従って、環の位数が十分に大きい場合、5パス方式の方が1回当たりの偽証確率を低減することが可能になり、少ない対話プロトコルの実行回数で、偽証確率を十分に小さくすることができる。
【0122】
例えば、偽証確率を1/2n以下にしたい場合、3パス方式においては、n/(log3−1)=1.701n回以上、対話プロトコルを実行する必要がある。一方、偽証確率を1/2n以下にしたい場合、5パス方式においては、n/(1−log(1+1/q))回以上、対話プロトコルを実行する必要がある。従って、q=24にすれば、同じセキュリティレベルを実現するのに必要な通信量は、3パス方式に比べ、5パス方式の方が少なくなるのである。
【0123】
[3−1:具体的なアルゴリズムの構成例(図7)]
まず、図7を参照しながら、5パス方式に係る具体的なアルゴリズムの構成例について紹介する。図7は、5パス方式に係る具体的なアルゴリズムの構成について説明するための説明図である。ここでは、公開鍵pkの一部として2次多項式の組(f1(x),…,fm(x))を利用する場合について考える。但し、2次多項式fi(x)は、上記の式(6)のように表現されるものとする。また、ベクトル(x1,…,xn)をxと表記し、2次多項式の組(f1(x),…,fm(x))を多変数多項式F(x)と表記することにする。
【0124】
3パス方式に係るアルゴリズムと同様、2つのベクトルt0∈Kn、e0∈Kmを用いて、多変数多項式F(x+r0)をマスクするために用いた多変数多項式F1(x)をF1(x)=G(x、t0)+e0のように表現する。この表現を用いると、多変数多項式F(x+r0)について、下記の式(23)で表現される関係が得られる。
【0125】
【数13】

【0126】
そのため、t1=ChA・r0+t0、e1=ChA・F(r0)+e0とすれば、マスク後の多変数多項式F2(x)=ChA・F(x+r0)+F1(x)も、2つのベクトルt1∈Kn、e1∈Kmにより表現することができる。これらの理由から、F1(x)=G(x,t0)+e0と設定すれば、Kn上のベクトル及びKm上のベクトルを用いてF1及びF2を表現できるようになり、通信に必要なデータサイズが少ない効率的なアルゴリズムを実現することが可能になる。
【0127】
なお、F2(或いはF1)からr0に関する情報が一切漏れることはない。例えば、e1及びt1(或いはe0及びt0)を与えられても、e0及びt0(或いはe1及びt1)を知らない限り、r0の情報を一切知ることはできない。従って、零知識性は担保される。以下、上記の論理に基づいて構築された5パス方式のアルゴリズムについて説明する。ここで説明する5パス方式のアルゴリズムは、以下のような鍵生成アルゴリズムGen、証明者アルゴリズムP、検証者アルゴリズムVにより構成される。
【0128】
(鍵生成アルゴリズムGen)
鍵生成アルゴリズムGenは、環K上で定義される多変数多項式f1(x1,…,xn),…,fm(x1,…,xn)、及びベクトルs=(s1,…,sn)∈Knを生成する。次に、鍵生成アルゴリズムGenは、y=(y1,…,ym)←(f1(s),…,fm(s))を計算する。そして、鍵生成アルゴリズムGenは、(f1,…,fm,y)を公開鍵pkに設定し、sを秘密鍵に設定する。なお、以下では、ベクトル(x1,…,xn)をxと表記し、多変数多項式の組(f1(x),…,fm(x))をF(x)と表記する。
【0129】
(証明者アルゴリズムP、検証者アルゴリズムV)
以下、図7を参照しながら、対話プロトコルの中で証明者アルゴリズムP及び検証者アルゴリズムVにより実行される処理について説明する。この対話プロトコルの中で、証明者は、秘密鍵sの情報を検証者に一切漏らさずに、「自身がy=F(s)を満たすsを知っていること」を検証者に示す。一方、検証者は、証明者がy=F(s)を満たすsを知っているか否かを検証する。なお、公開鍵pkは、検証者に公開されているものとする。また、秘密鍵sは、証明者により秘密に管理されているものとする。以下、図7に示したフローチャートに沿って説明を進める。
【0130】
工程#1:
図7に示すように、まず、証明者アルゴリズムPは、ランダムにベクトルr0∈Kn、t0∈Kn、e0∈Kmを生成する。次いで、証明者アルゴリズムPは、r1←s−r0を計算する。この計算は、秘密鍵sをベクトルr0によりマスクする操作に相当する。次いで、証明者アルゴリズムPは、ベクトルr0,t0,e0のハッシュ値c0を生成する。つまり、証明者アルゴリズムPは、c0←H(r0,t0,e0)を計算する。次いで、証明者アルゴリズムPは、G(t0,r1)+e0及びr1のハッシュ値c1を生成する。つまり、証明者アルゴリズムPは、c0←H(r1,G(t0,r1)+e0)を計算する。工程#1で生成されたメッセージ(c0,c1)は、検証者アルゴリズムVに送られる。
【0131】
工程#2:
メッセージ(c0,c1)を受け取った検証者アルゴリズムVは、q通り存在する環Kの元からランダムに1つの数ChAを選択し、選択した数ChAを証明者アルゴリズムPに送る。
【0132】
工程#3:
数ChAを受け取った証明者アルゴリズムPは、t1←ChA・r0−t0を計算する。さらに、証明者アルゴリズムPは、e1←ChA・F(r0)−e0を計算する。そして、証明者アルゴリズムPは、t1及びe1を検証者アルゴリズムVに送る。
【0133】
工程#4:
t1及びe1を受け取った検証者アルゴリズムVは、2つの検証パターンのうち、どちらの検証パターンを利用するかを選択する。例えば、検証者アルゴリズムVは、検証パターンの種類を表す2つの数値{0,1}の中から1つの数値を選択し、選択した数値を要求ChBに設定する。この要求ChBは証明者アルゴリズムPに送られる。
【0134】
工程#5:
要求ChBを受け取った証明者アルゴリズムPは、受け取った要求ChBに応じて検証者アルゴリズムVに送り返す返答Rspを生成する。ChB=0の場合、証明者アルゴリズムPは、返答Rsp=r0を生成する。ChB=1の場合、証明者アルゴリズムPは、返答Rsp=r1を生成する。工程#5で生成された返答Rspは、検証者アルゴリズムVに送られる。
【0135】
工程#6:
返答Rspを受け取った検証者アルゴリズムVは、受け取った返答Rspを利用して以下の検証処理を実行する。
【0136】
ChB=0の場合、検証者アルゴリズムVは、r0←Rspを実行する。そして、検証者アルゴリズムVは、c0=H(r0,ChA・r0−t1,ChA・F(r0)−e1)の等号が成り立つか否かを検証する。検証者アルゴリズムVは、この検証が成功した場合に認証成功を示す値1を出力し、検証に失敗があった場合に認証失敗を示す値0を出力する。
【0137】
ChB=1の場合、検証者アルゴリズムVは、r1←Rspを実行する。そして、検証者アルゴリズムVは、c1=H1(r1,ChA・(y−F(r1))−G(t1,r1)−e1)の等号が成り立つか否かを検証する。検証者アルゴリズムVは、この検証が成功した場合に認証成功を示す値1を出力し、検証に失敗があった場合に認証失敗を示す値0を出力する。
【0138】
以上、5パス方式に係る効率的なアルゴリズムの構成例について説明した。
【0139】
[3−2:並列化アルゴリズムの構成例(図8)]
次に、図8を参照しながら、図7に示した5パス方式のアルゴリズムを並列化する方法について説明する。なお、鍵生成アルゴリズムGenの構成については説明を省略する。
【0140】
先に述べた通り、5パス方式に係る対話プロトコルを適用すれば、偽証が成功する確率を(1/2+1/q)以下に抑制することができる。従って、この対話プロトコルを2回実行すれば、偽証が成功する確率を(1/2+1/q)2以下に抑制することができる。さらに、この対話プロトコルをN回実行すると、偽証が成功する確率は(1/2+1/q)Nとなり、Nを十分に大きい数(例えば、N=80)にすれば、偽証が成功する確率は無視できる程度に小さくなる。
【0141】
対話プロトコルを複数回実行する方法としては、例えば、メッセージ、要求、返答のやり取りを逐次的に複数回繰り返す直列的な方法と、1回分のやり取りで複数回分のメッセージ、要求、返答のやり取りを行う並列的な方法とが考えられる。さらに、直列的な方法と並列的な方法とを組み合わせたハイブリッド型の方法も考えられる。ここでは、5パス方式に係る上記の対話プロトコルを並列的に実行するアルゴリズム(以下、並列化アルゴリズム)について説明する。
【0142】
工程#1:
図8に示すように、まず、証明者アルゴリズムPは、i=1〜Nについて処理(1)〜処理(4)を実行する。
処理(1):証明者アルゴリズムPは、ランダムにベクトルr0i,t0i∈Kn及びe0i∈Kmを生成する。
処理(2):証明者アルゴリズムPは、r1i←s−r0iを計算する。この計算は、秘密鍵sをベクトルr0iによりマスクする操作に相当する。
処理(3):証明者アルゴリズムPは、c0i←H(r0i,t0i,e0i)を計算する。
処理(4):証明者アルゴリズムPは、c1i←H(r1i,G(t0i,r1i)+e0i)を計算する。
i=1〜Nについて処理(1)〜処理(4)を実行した後、証明者アルゴリズムPは、ハッシュ値Cmt←H(c01,c11,…,c0N,c1N)を実行する。そして、工程#1で生成されたハッシュ値Cmtは、検証者アルゴリズムVに送られる。
【0143】
工程#2:
ハッシュ値Cmtを受け取った検証者アルゴリズムVは、i=1〜Nのそれぞれについて、q通り存在する環Kの元からランダムに1つの数ChAiを選択し、選択した数ChAi(i=1〜N)を証明者アルゴリズムPに送る。
【0144】
工程#3:
数ChAi(i=1〜N)を受け取った証明者アルゴリズムPは、i=1〜Nのそれぞれについて、t1i←ChAi・r0i−t0iを計算する。さらに、証明者アルゴリズムPは、i=1〜Nのそれぞれについて、e1i←ChAi・F(r0i)−e0iを計算する。次いで、証明者アルゴリズムPは、ハッシュ値d←H(t11,e11,…,t1N,e1N)を計算する。そして、証明者アルゴリズムPは、ハッシュ値dを検証者アルゴリズムVに送る。
【0145】
工程#4:
ハッシュ値dを受け取った検証者アルゴリズムVは、i=1〜Nのそれぞれについて、2つの検証パターンのうち、どちらの検証パターンを利用するかを選択する。例えば、検証者アルゴリズムVは、検証パターンの種類を表す2つの数値{0,1}の中から1つの数値を選択し、選択した数値を要求ChBiに設定する。要求ChBi(i=1〜N)は証明者アルゴリズムPに送られる。
【0146】
工程#5:
要求ChBi(i=1〜N)を受け取った証明者アルゴリズムPは、i=1〜Nについて、受け取った要求ChBiに応じて検証者アルゴリズムVに送り返す返答Rspiを生成する。ChBi=0の場合、証明者アルゴリズムPは、返答Rspi=(r0i,t0i,e0i,c1i)を生成する。ChBi=1の場合、証明者アルゴリズムPは、返答Rspi=(r1i,t1i,e1i,c0i)を生成する。工程#5で生成された返答Rspi(i=1〜N)は、検証者アルゴリズムVに送られる。
【0147】
工程#6:
返答Rspi(i=1〜N)を受け取った検証者アルゴリズムVは、受け取った返答Rspi(i=1〜N)を利用して以下の処理(1)及び処理(2)を実行する。
【0148】
処理(1):ChBi=0の場合、検証者アルゴリズムVは、(r0i,t0i,e0i,c1i)←Rspiを実行する。そして、検証者アルゴリズムVは、c0i=H(r0i,t0i,e0i)を計算する。さらに、検証者アルゴリズムVは、t1i←ChAi・r0i+t0i、及びe1i←ChAi・F(r0i)−e0iを計算する。そして、検証者アルゴリズムVは、(c0i,c1i,t1i,e1i)を保持する。
【0149】
処理(2):ChBi=1の場合、検証者アルゴリズムVは、(r1i,t1i,e1i,c0i)←Rspiを実行する。そして、検証者アルゴリズムVは、c1i=H(r1i,ChAi・(y−F(r1i))−G(t1i,r1i)−e1i)を計算する。そして、検証者アルゴリズムVは、(c0i,c1i,t1i,e1i)を保持する。
【0150】
i=1〜Nについて処理(1)及び処理(2)を実行した後、検証者アルゴリズムVは、Cmt=H(c01,c11,…,c0N,c1N)の等号が成り立つか否かを検証する。さらに、検証者アルゴリズムVは、d=H(t11,e11,…,t1N,e1N)の等号が成り立つか否かを検証する。そして、検証者アルゴリズムVは、これらの検証が全て成功した場合に認証成功を示す値1を出力し、検証に失敗があった場合に認証失敗を示す値0を出力する。
【0151】
以上、5パス方式に係る効率的な並列化アルゴリズムの構成例について説明した。
【0152】
[3−3:3次多変数多項式に基づくアルゴリズムの構成例]
さて、3パス方式の場合と同様、環R上の3次多項式flを利用した効率的なアルゴリズムの構築方法について検討してみたい。3次多項式flを上記の式(12)のように表現した場合に、Gx(x,y)及びGy(x,y)がx及びyについて線形になることについては式(14)と式(15)より分かる。
【0153】
そこで、上記の性質を利用し、新たな変数r0,r1,t0,u0,e0を導入して、公開鍵F(s)をChA倍した項を分割する。多項式Gx,Gyがそれぞれxとyについて線形であるから、変数r0,r1,t0,u0,e0を用いて、下記の式(24)〜式(27)の関係が成り立つ。また、下記の式(24)〜式(27)は、ChAに依存する第1の部分と、ChAに依存しない第2の部分とに分けることができる。但し、第1の部分は、(r1,t1,u1,e1)で再現可能である。また、第2の部分は、(r0,t1,u1,e1)で再現可能である。
【0154】
例えば、下記の式(32)に含まれる「e0,Gx(t0,r1)」、下記の式(33)に含まれる「t0」、下記の式(26)に含まれる「u0」、下記の式(27)に含まれる「e0,Gy(r0,u0)」は第1の部分である。一方、下記の式(24)に含まれる「ChA・F(r0+r1),e1,ChA・F(r1),Gx(t1,r1)」、下記の式(25)に含まれる「ChA・r0,t1」、下記の式(34)に含まれる「ChA・r1,u1」、下記の式(27)に含まれる「ChA・F(r0),Gy(r0,u1),e1」は第2の部分である。
【0155】
また、秘密鍵sの定義及び下記の式(24)〜式(27)の関係から、(r1,t1,u1,e1)、(r0,t1,u1,e1)のいずれか1つを用いても秘密鍵sは得られないことが保証される。これらの性質を利用すると、例えば、環R上の3次多項式flを利用した効率的なアルゴリズム(以下、拡張アルゴリズム)を構築することができる。
【0156】
【数14】

【0157】
以下、具体的な拡張アルゴリズムの構成例について説明する。拡張アルゴリズムの設計に関する基本的なポイントは、下記の式(28)及び式(29)で表現されるメッセージを検証者に送ること、及び検証者が選択したChAについて、ChAに依存する部分(第1の部分)に関する検証を行うことの2点である。但し、「メッセージを生成する際に利用したr0及びr1を、検証の際に別のr0及びr1にすり替えられることを防ぐ」ために、r0及びr1に関する検証を追加した構成例を以下で紹介する。
【0158】
【数15】

【0159】
以下、図9を参照しながら、5パス方式に係る拡張アルゴリズムの基本構成について説明する。なお、鍵生成アルゴリズムGenの構成については説明を省略する。
【0160】
工程#1:
図9に示すように、証明者アルゴリズムPは、ランダムにベクトルr0,t0,u0∈Kn及びe0∈Kmを生成する。次いで、証明者アルゴリズムPは、r1←s−r0を計算する。この計算は、秘密鍵sをベクトルr0によりマスクする操作に相当する。次いで、証明者アルゴリズムPは、c0←H(r0,t0,e0−Gy(r0,u0))を計算する。次いで、証明者アルゴリズムPは、c1←H(r1,u0,Gx(t0,r1)+e0)を計算する。工程#1で生成されたメッセージ(c0,c1)は、検証者アルゴリズムVに送られる。
【0161】
工程#2:
メッセージ(c0,c1)を受け取った検証者アルゴリズムVは、ランダムに数ChAを選択する。この数ChAは証明者アルゴリズムPに送られる。
【0162】
工程#3:
数ChAを受け取った証明者アルゴリズムPは、t1←ChA・r0−t0を計算する。次いで、証明者アルゴリズムPは、u1←ChA・r1−u0を計算する。次いで、証明者アルゴリズムPは、e1←ChA・F(r0)+ChA・Gy(r0,r1)−e0を計算する。工程#3で生成された(t1,u1,e1)は、検証者アルゴリズムVに送られる。
【0163】
工程#4:
(t1,u1,e1)を受け取った検証者アルゴリズムVは、2つの検証パターンのうち、どの検証パターンを利用するかを選択する。例えば、検証者アルゴリズムVは、検証パターンの種類を表す2つの数値{0,1}の中から1つの数値を選択し、選択した数値を要求ChBに設定する。この要求ChBは証明者アルゴリズムPに送られる。
【0164】
工程#5:
要求ChBを受け取った証明者アルゴリズムPは、受け取った要求ChBに応じて検証者アルゴリズムVに送る返答Rspを生成する。ChB=0の場合、証明者アルゴリズムPは、返答Rsp=r0を生成する。ChB=1の場合、証明者アルゴリズムPは、返答Rsp=r1を生成する。工程#5で生成された返答Rspは、検証者アルゴリズムVに送られる。
【0165】
工程#6:
返答Rspを受け取った検証者アルゴリズムVは、受け取った返答Rspを利用して以下の検証処理を実行する。
【0166】
ChB=0の場合、検証者アルゴリズムVは、c0=H(r0,ChA・r0−t1,ChA・F(r0)+Gy(r0,u1)−e1)の等号が成り立つか否かを検証する。検証者アルゴリズムVは、この検証が成功した場合に認証成功を示す値1を出力し、検証に失敗があった場合に認証失敗を示す値0を出力する。
【0167】
ChB=1の場合、検証者アルゴリズムVは、c1=H(r1,ChA・r1−u1,ChA・(y−F(r1))−Gx(t1,r1)−e1)の等号が成り立つか否かを検証する。検証者アルゴリズムVは、この検証が成功した場合に認証成功を示す値1を出力し、検証に失敗があった場合に認証失敗を示す値0を出力する。
【0168】
以上、5パス方式に係る拡張アルゴリズムの構成例について説明した。3次多項式を利用していることにより、より高い安全性が実現される。
【0169】
<4:電子署名方式への変形>
次に、上記の公開鍵認証方式を電子署名方式へと変形する方法を紹介する。
【0170】
公開鍵認証方式のモデルにおける証明者を電子署名方式における署名者に対応させると、証明者のみが検証者を納得させられるという点において、電子署名方式のモデルと近似していることが容易に理解されよう。こうした考えに基づき、上述した公開鍵認証方式を電子署名方式へと変形する方法について説明する。
【0171】
[4−1:3パスの公開鍵認証方式から電子署名方式への変形(図10)]
まず、3パスの公開鍵認証方式から電子署名方式への変形について説明する。
【0172】
図10に示すように、3パス方式に係る効率的なアルゴリズム(例えば、図5を参照)は、3回の対話及び4つの工程#1〜工程#4で表現される。
【0173】
工程#1は、i=1〜Nについて、ai=(r0i,t0i,e0i,r1i,t1i,e1i,c0i,c1i,c2i)を生成する処理(1)と、Cmt←H(c01,c11,c21,…,c0N,c1N,c2N)を計算する処理(2)とで構成される。工程#1で証明者アルゴリズムPにより生成されたCmtは、検証者アルゴリズムVへと送られる。
【0174】
工程#2は、Ch1,…,ChNを選択する処理で構成される。工程#2で検証者アルゴリズムVにより選択されたCh1,…,ChNは、証明者アルゴリズムPへと送られる。
【0175】
工程#3は、Ch1,…,ChN及びa1,…,aNを用いてRsp1,…,RspNを生成する処理で構成される。この処理をRspi←Select(Chi,ai)と表現する。工程#3で証明者アルゴリズムPにより生成されたRsp1,…,RspNは、検証者アルゴリズムVへと送られる。
【0176】
工程#4は、Ch1,…,ChN及びRsp1,…,RspNを用いてc01,c11,c21,…,c0N,c1N,c2Nを再生する処理(1)と、再生したc01,c11,c21,…,c0N,c1N,c2Nを用いてCmt=H(c01,c11,c21,…,c0N,c1N,c2N)を検証する処理(2)とで構成される。
【0177】
上記の工程#1〜工程#4で表現される公開鍵認証方式のアルゴリズムは、図10に示すような署名生成アルゴリズムSig及び署名検証アルゴリズムVerに変形される。
【0178】
(署名生成アルゴリズムSig)
まず、署名生成アルゴリズムSigの構成について述べる。署名生成アルゴリズムSigは、以下の処理(1)〜処理(5)で構成される。
【0179】
処理(1):署名生成アルゴリズムSigは、ai=(r0i,t0i,e0i,r1i,t1i,e1i,c0i,c1i,c2i)を生成する。
処理(2):署名生成アルゴリズムSigは、Cmt←H(c01,c11,c21,…,c0N,c1N,c2N)を計算する。
処理(3):署名生成アルゴリズムSigは、(Ch1,…,ChN)←H(M,Cmt)を計算する。このMは、署名を付与する文書である。
処理(4):署名生成アルゴリズムSigは、Rspi←Select(Chi,ai)を計算する。
処理(5):署名生成アルゴリズムSigは、(Cmt,Rsp1,…,RspN)を署名に設定する。
【0180】
(署名検証アルゴリズムVer)
次に、署名検証アルゴリズムVerの構成について述べる。署名検証アルゴリズムVerは、以下の処理(1)〜処理(3)で構成される。
【0181】
処理(1):署名検証アルゴリズムVerは、(Ch1,…,ChN)←H(M,Cmt)を計算する。
処理(2):署名検証アルゴリズムVerは、Ch1,…,ChN及びRsp1,…,RspNを用いてc01,c11,c21,…,c0N,c1N,c2Nを生成する。
処理(3):署名検証アルゴリズムVerは、再生したc01,c11,c21,…,c0N,c1N,c2Nを用いてCmt=H(c01,c11,c21,…,c0N,c1N,c2N)を検証する。
【0182】
以上説明したように、公開鍵認証方式のモデルにおける証明者を電子署名方式における署名者に対応させることで、公開鍵認証方式のアルゴリズムを電子署名方式のアルゴリズムへと変形することが可能になる。
【0183】
[4−2:5パスの公開鍵認証方式から電子署名方式への変形(図11)]
次に、5パスの公開鍵認証方式から電子署名方式への変形について説明する。
【0184】
図11に示すように、5パス方式に係る効率的なアルゴリズム(例えば、図8を参照)は、5回の対話及び6つの工程#1〜工程#6で表現される。
【0185】
工程#1は、i=1〜Nについて、ai=(r0i,t0i,e0i,r1i,t1i,e1i,c0i,c1i)を生成する処理(1)と、Cmt←H(c01,c11,…,c0N,c1N)を計算する処理(2)とで構成される。工程#1で証明者アルゴリズムPにより生成されたCmtは、検証者アルゴリズムVへと送られる。
【0186】
工程#2は、ChA1,…,ChANを選択する処理で構成される。工程#2で検証者アルゴリズムVにより選択されたChA1,…,ChANは、証明者アルゴリズムPへと送られる。
【0187】
工程#3は、i=1〜Nについて、bi=(t1i,e1i)を生成する処理、及びd=H(t11,e11,…,t1N,e1N)を生成する処理で構成される。工程#3で証明者アルゴリズムPにより生成されたdは、検証者アルゴリズムVへと送られる。
【0188】
工程#4は、ChB1,…,ChBNを選択する処理で構成される。工程#4で検証者アルゴリズムVにより選択されたChB1,…,ChBNは、証明者アルゴリズムPへと送られる。
【0189】
工程#5は、ChB1,…,ChBN,a1,…,aN,b1,…,bNを用いてRsp1,…,RspNを生成する処理で構成される。この処理をRspi←Select(ChBi,ai,bi)と表現する。工程#5で証明者アルゴリズムPにより生成されたRsp1,…,RspNは、検証者アルゴリズムVへと送られる。
【0190】
工程#6は、ChA1,…,ChAN,ChB1,…,ChBN,Rsp1,…,RspNを用いてc01,c11,…,c0N,c1N,t11,e11,…,t1N,e1Nを再生する処理と、再生したc01,c11,…,c0N,c1Nを用いてCmt=H(c01,c11,…,c0N,c1N)を検証する処理と、d=H(t11,e11,…,t1N,e1N)を検証する処理とで構成される。
【0191】
上記の工程#1〜工程#6で表現される公開鍵認証方式のアルゴリズムは、図11に示すような署名生成アルゴリズムSig及び署名検証アルゴリズムVerに変形される。
【0192】
(署名生成アルゴリズムSig)
まず、署名生成アルゴリズムSigの構成について述べる。署名生成アルゴリズムSigは、以下の処理(1)〜処理(7)で構成される。
【0193】
処理(1):署名生成アルゴリズムSigは、ai=(r0i,t0i,e0i,r1i,t1i,e1i,c0i,c1i)を生成する。
処理(2):署名生成アルゴリズムSigは、Cmt←H(c01,c11,…,c0N,c1N)を計算する。
処理(3):署名生成アルゴリズムSigは、(ChA1,…,ChAN)←H(M,Cmt)を計算する。このMは、署名を付与する文書である。
処理(4):署名生成アルゴリズムSigは、i=1〜Nについて、bi=(t1i,e1i)を生成する。さらに、署名生成アルゴリズムSigは、d=H(t11,e11,…,t1N,e1N)を算出する。
処理(5):署名生成アルゴリズムSigは、(ChB1,…,ChBN)←H(M,Cmt,ChA1,…,ChAN,d)を計算する。なお、(ChB1,…,ChBN)←H(ChA1,…,ChAN,d)と変形してもよい。
処理(6):署名生成アルゴリズムSigは、Rspi←Select(ChBi,ai,bi)を計算する。
処理(7):署名生成アルゴリズムSigは、(Cmt,d,Rsp1,…,RspN)を電子署名に設定する。
【0194】
(署名検証アルゴリズムVer)
次に、署名検証アルゴリズムVerの構成について述べる。署名検証アルゴリズムVerは、以下の処理(1)〜処理(4)で構成される。
【0195】
処理(1):署名検証アルゴリズムVerは、(ChA1,…,ChAN)←H(M,Cmt)を計算する。
処理(2):署名検証アルゴリズムVerは、(ChB1,…,ChBN)←H(M,Cmt,ChA1,…,ChAN,d)を計算する。なお、署名検証アルゴリズムVerが実行する処理(5)において、(ChB1,…,ChBN)←H(ChA1,…,ChAN,d)と変形した場合、署名検証アルゴリズムVerは、(ChB1,…,ChBN)←H(ChA1,…,ChAN,d)を計算する。
処理(3):署名検証アルゴリズムVerは、ChA1,…,ChAN,ChB1,…,ChBN,Rsp1,…,RspNを用いてt11,e11,…,t1N,e1N,c01,c11,…,c0N,c1Nを生成する。
処理(4):署名検証アルゴリズムVerは、再生したc01,c11,…,c0N,c1Nを用いてCmt=H(c01,c11,…,c0N,c1N)及びd=H(t11,e11,…,t1N,e1N,)を検証する。
【0196】
以上説明したように、公開鍵認証方式のモデルにおける証明者を電子署名方式における署名者に対応させることで、公開鍵認証方式のアルゴリズムを電子署名方式のアルゴリズムへと変形することが可能になる。
【0197】
<5:署名検証に要するメモリ量の削減方法について>
ところで、上述した電子署名方式のアルゴリズムにおいては、署名検証アルゴリズムVerが電子署名全体を受信した後で署名検証の処理を実行していた。しかし、上述した電子署名方式の場合、電子署名のデータサイズが比較的大きい。そのため、RFID(Radio Frequency IDentification)など、少ないメモリ容量しか持たないデバイスを用いて認証を行う場合には、メモリの空き容量や認証処理中のメモリ使用率などに気を配る必要があった。また、十分なメモリ容量を持たないデバイスを利用する場合、認証を行うことができない場合も想定される。そこで、本件発明者は、署名検証に要するメモリ量の削減方法を考案した。
【0198】
[5−1:ハッシュ関数の構造について(図12)]
まず、本件発明者は、ハッシュ関数の構造に注目した。多くの場合、ハッシュ関数は、入力をブロック単位に区切り、ブロック単位で順次処理を進める構造を有している。例えば、SHA−1の場合、ハッシュ関数は、図12に示すような構造を有している。図12に示すハッシュ関数は、パディング済みの入力MをZ個のブロックm1,…,mZに区切り、インデックスjをインクリメントしながら、逐次的に、ブロックmjを初期値IV又は中間値CVjと共に所定の関数CFに作用させてハッシュ値を生成する。従って、中間値CVjが得られた時点で、それ以前に利用したブロックは不要になる。そこで、この特性を利用し、アルゴリズムの実行に必要なメモリ量を効果的に削減する仕組み(以下、メモリ削減方法)を考案した。以下、この仕組みを上述した電子署名方式に適用する方法について説明する。
【0199】
[5−2:3パス方式に基づく電子署名方式への適用例(図14)]
まず、図10に示した3パス方式に基づく電子署名方式のアルゴリズムに上記のメモリ削減方法を適用する方法について説明する。
【0200】
(通常の実装方法:図13)
通常、上述した電子署名方式に係る署名検証アルゴリズムVerは、図13に示すように、電子署名を構成する(Cmt,Rsp1,…,RspN)を1度に受信する(S101)。次いで、署名検証アルゴリズムVerは、(Ch1,…,ChN)←H(M,Cmt)を実行する(S102)。次いで、署名検証アルゴリズムVerは、(c01,c11,c21,…,c0N,c1N,c2N)←Reproduce(Ch1,…,ChN;Rsp1,…,RspN)を実行する(S103)。次いで、署名検証アルゴリズムVerは、Cmt=H(c01,c11,c21,…,c0N,c1N,c2N)を検証し(S104)、署名検証に係る一連の処理を終了する。
【0201】
(メモリ削減方法:図14)
通常の実装方法の場合、図13のステップS101のように、一度に電子署名を受信すると、ステップS103の処理が完了するまで(Rsp1,…,RspN)を保持しておくためのメモリが必要になる。しかし、図5のアルゴリズム構成から分かるように、ステップS103で実行する(c0i,c1i,c2i)の再生には(Chi;Rspi)以外の情報を利用しない。また、図12に示したハッシュ関数の構造を考慮すると、ステップS104において実行されるハッシュ関数の計算はブロック単位で分割して実行できることが分かる。そこで、署名検証に係る処理の構成を図14に示すような構成に改良する。
【0202】
図14に示す構成の場合、署名検証アルゴリズムVerは、まず、電子署名に含まれるCmtだけを受信する(S111)。次いで、署名検証アルゴリズムVerは、(Ch1,…,ChN)←H(M,Cmt)を実行する(S112)。次いで、署名検証アルゴリズムVerは、i=1〜Nについて、iをインクリメントさせながら逐次的にステップS113〜S115の処理を実行する。
【0203】
ステップS113において、署名検証アルゴリズムVerは、Rspiを受信する(S113)。次いで、署名検証アルゴリズムVerは、受信したRspiを用いて、(c0i,c1i,c2i)←Reproduce(Chi;Rspi)を実行する(S114)。ステップS114の処理を実行した後、Chi及びRspiは不要になる。そこで、署名検証アルゴリズムVerは、ステップS114の処理を実行後にChi及びRspiをメモリから消去する。
【0204】
次いで、署名検証アルゴリズムVerは、tmpi←Hi(tmpi−1;c0i,c1i,c2i)を実行する(S115)。なお、関数Hiは、ハッシュ関数Hの内部でc0i,c1i,c2iまで計算した際に生成される中間値を出力する関数である。実際には選択したハッシュ関数に応じて関数Hiの入力サイズは異なるため必要に応じて、ビットを付加するなどの適切な入力長の補正が行われる。関数Hiを用いると、ハッシュ関数Hは、以下に示す処理(1)〜処理(3)で構成されたアルゴリズムにより表現される。そして、tmpNがハッシュ関数Hの最終的な出力(ハッシュ値)となる。実際にはハッシュ関数の仕様に応じて、最終処理においてパディングの追加処理を行う。
【0205】
処理(1):tmp0←空文字列
処理(2):
for i=1 to N
tmpi←Hi(tmpi−1;c0i,c1i,c2i)
end for
処理(3):output tmpN
【0206】
i=1〜Nについて、ステップS113〜S115の処理を実行した後、署名検証アルゴリズムVerは、Cmt=tmpNが成り立つか否かを検証し(S116)、署名検証に係る一連の処理を終了する。上記のように、署名検証アルゴリズムVerは、ステップS113〜S115の処理を繰り返し実行する過程で不要になった情報をメモリかた消去する。そのため、署名検証に要するメモリ量は最小限に抑えられる。その結果、少ないメモリ容量しか持たないデバイスでも、上記の署名検証が可能になる。
【0207】
[5−3:5パス方式に基づく電子署名方式への適用例(図16)]
次に、図11に示した5パス方式に基づく電子署名方式のアルゴリズムに上記のメモリ削減方法を適用する方法について説明する。
【0208】
(通常の実装方法:図15)
通常、上述した電子署名方式に係る署名検証アルゴリズムVerは、図15に示すように、電子署名を構成する(Cmt,d,Rsp1,…,RspN)を1度に受信する(S121)。次いで、署名検証アルゴリズムVerは、(ChA1,…,ChAN)←H(M,Cmt)を実行する(S122)。次いで、署名検証アルゴリズムVerは、(ChB1,…,ChBN)←H(M,Cmt,ChA1,…,ChAN,d)を実行する(S123)。次いで、署名検証アルゴリズムVerは、(c01,c11,…,c0N,c1N,d11,e11,…,d1N,e1N)←Reproduce(ChA1,…,ChAN,ChB1,…,ChBN;Rsp1,…,RspN)を実行する(S124)。次いで、署名検証アルゴリズムVerは、Cmt=H(c01,c11,…,c0N,c1N)とd=H(d11,e11,…,d1N,e1N)を検証し(S125)、署名検証に係る一連の処理を終了する。
【0209】
(メモリ削減方法:図16)
図15のステップS121のように、一度に電子署名を受信すると、ステップS124の処理が完了するまで(Rsp1,…,RspN)を保持しておくためのメモリが必要になる。しかしながら、図8のアルゴリズム構成から分かるように、ステップS124で実行する(c0i,c1i,d1i,e1i)の再生には(ChAi,ChBi;Rspi)以外の情報を利用しない。また、図12に示したハッシュ関数の構造を考慮すると、ステップS125において実行されるハッシュ関数の計算はブロック単位で分割して実行できることが分かる。そこで、署名検証に係る処理の構成を図16に示すような構成に改良する。
【0210】
図16に示す構成の場合、署名検証アルゴリズムVerは、まず、電子署名に含まれるCmtだけを受信する(S131)。次いで、署名検証アルゴリズムVerは、(ChA1,…,ChAN)←H(M,Cmt)を実行する(S132)。
【0211】
次いで、署名検証アルゴリズムVerは、dを受信する(S133)。次いで、署名検証アルゴリズムVerは、受信したdを用いて、(ChB1,…,ChBN)←H(M,Cmt,ChA1,…,ChAN,d)を実行する(S134)。ステップS134の処理を実行した後、dは不要になる。そこで、署名検証アルゴリズムVerは、ステップS134の処理を実行後にdをメモリから消去する。次いで、署名検証アルゴリズムVerは、i=1〜Nについて、iをインクリメントさせながら逐次的にステップS135〜S137の処理を実行する。
【0212】
ステップS135において、署名検証アルゴリズムVerは、Rspiを受信する(S135)。次いで、署名検証アルゴリズムVerは、受信したRspiを用いて、(c0i,c1i,t1i,e1i)←Reproduce(ChAi,ChBi,Rspi)を実行する(S136)。ステップS136の処理を実行した後、ChAi、ChBi及びRspiは不要になる。そこで、署名検証アルゴリズムVerは、ステップS136の処理を実行後にChAi、ChBi及びRspiをメモリから消去する。
【0213】
次いで、署名検証アルゴリズムVerは、tmpi←Hi(tmpi−1;c0i,c1i)とtmpi’←Hi(tmpi−1’;t1i,e1i)を実行する(S137)。i=1〜Nについて、ステップS135〜S137の処理を実行した後、署名検証アルゴリズムVerは、Cmt=tmpNとd=tmpN’が成り立つか否かを検証し(S138)、署名検証に係る一連の処理を終了する。上記のように、署名検証アルゴリズムVerは、ステップS135〜S137の処理を繰り返し実行する過程で不要になった情報をメモリから消去する。そのため、署名検証に要するメモリ量は最小限に抑えられる。その結果、少ないメモリ容量しか持たないデバイスでも、上記の署名検証が可能になる。
【0214】
以上、署名検証に要するメモリ量の削減方法について説明した。
【0215】
<6:2進数の乱数列から3進数の乱数列を抽出する方法について>
ところで、3パス方式に基づく公開鍵認証方式のアルゴリズムにおいて、3進数の一様乱数をN個以上生成する場面が存在する。しかし、3進数の一様乱数を生成する優れた乱数生成器は一般的ではない。そのため、2進数の一様乱数を生成する優れた乱数生成器を用いて3進数の一様乱数を生成する方法を考える必要がある。そこで、本件発明者は、2進数の一様乱数から3進数の一様乱数を効率的に生成する方法を考案した。以下、この方法について詳細に説明する。なお、以下の説明において、l進表現(lは2又は3)で表された1つの数を1シンボルと数えることにする。
【0216】
[6−1:抽出方法#1(2ビット区切り)(図17)]
まず、図17を参照しながら、Mビットの2進数を2ビットずつ区切って3進数を抽出する方法(以下、抽出方法#1)を紹介する。図17に示すように、2進表現の乱数列を2ビットずつ区切ると、M/2個の2ビットの乱数が得られる。例えば、「00」を3進数の「0」、「01」を3進数の「1」、「10」を3進数の「2」に対応付けると、2ビット単位の2進表現の乱数列から3進数の乱数列を得ることができる。但し、2ビットの値「11」は除外する。つまり、抽出方法#1は、2進数2シンボルで表現される22通りの数の中から、3進数1シンボルで表現される31通りの数を抽出する方法である。従って、N個以上の3進数が抽出できない確率P1は、下記の式(30)のようになる。
【0217】
【数16】

【0218】
[6−2:抽出方法#2(区切りなし)(図18)]
次に、図18を参照しながら、2進数Mシンボルの乱数を区切らずに利用して3進数Lシンボルの乱数を抽出する方法(以下、抽出方法#2)を紹介する。但し、Lは、3L≦2Mとなる最大の整数である。2進数Mシンボルで表現可能な数は、2M通り存在する。一方、3進数Lシンボルで表現可能な数は、3L通りしか存在しない。そのため、2進数Mシンボルで表現される2M通りの数のうち、2M−3L通りの数は、3進表現の乱数として利用されない。従って、N個以上の3進数が抽出できない確率P2は、下記の式(31)のようになる。
【0219】
【数17】

【0220】
[6−3:抽出方法#3(kビット区切り)(図19)]
上記の抽出方法#1は、最小の区切り単位で2進表現の乱数列を区切る方法である。一方、上記の抽出方法#2は、(Mビット区切りと考えられるため)最大の区切り単位で2進表現の乱数列を区切る方法である。上記の式(30)及び式(31)から分かるように、区切る長さに応じて、N個以上の3進数が抽出できない確率は異なる。因みに、図19に示すように、kビット単位で2進Mシンボルの乱数列を区切った場合、N個以上の3進数が抽出できない確率P3は、下記の式(32)のようになる。
【0221】
【数18】

【0222】
N個以上の3進数が抽出できない確率P3を最小化することができれば、最も効率よく3進表現の乱数列を抽出できることになる。例えば、M=512、N=140の場合、k=8のときに確率P3が最小となる。
【0223】
(6−3−1:基本構成(図20))
ここで、図20を参照しながら、2進Mシンボルの乱数列から3進Lシンボルの乱数列を抽出する処理の流れについて説明する。図20に示すように、まず、2進Mシンボルの乱数列が生成される(S201)。次いで、2進Mシンボルの乱数列が、kビット単位に区切られる(S202)。次いで、kビット単位で区切られたビット列X2kのうち、X2k≦3Lとなるビット列が抽出される(S203)。次いで、抽出されたビット列が、3進数表現で出力され(S204)、一連の処理が終了する。
【0224】
(6−3−2:追加抽出方法(図21))
上記の式(15)で表現される確率P3が最小となる区切りの長さkを算出し、図20に示したアルゴリズムを実行することにより、2進表現の乱数列から3進表現の乱数列を効率的に抽出することが可能になる。しかし、本件発明者は、図20のステップS204においてX2k>3Lとなるビット列が利用されない点に注目し、3進表現の乱数列をより効率的に抽出する方法を考案した。以下、この方法について、図21を参照しながら説明する。
【0225】
この方法は、図20のステップS204で抽出されなかったビット列を利用して、3進表現のシンボル列を抽出する方法である。図21に示すように、まず、図20のステップS204で抽出されなかった、X2k>3Lとなるビット列の組(例えば、ビット列の組をy1y2…yN’と表現すると、個々のビット列yiは3L≦yi<2k)が抽出される(S211)。次いで、抽出したビット列yiからそれぞれ3Lが減算され、新たなビット列の組(例えば、新たなビット列の組をz1z2…zN’と表現すると、個々のビット列zi=yi−3Lは0≦zi<2k−3L)が算出される(S212)。
【0226】
次いで、新たなビット列の組から、ビット列XがX<3L’となるものが抽出される(S213)。但し、L’は、3L’≦2k−3Lとなる最大の整数である。次いで、ステップS213で抽出されたビット列が3進表現で出力され(S214)、一連の処理が終了する。このアルゴリズムを適用することにより、確率3L’/(2k−3L)で新たにL’個の3進数を抽出することが可能になる。なお、この方法を再帰的に用いることで、さらに多くの3進数を抽出することができる。つまり、ステップS213でビット列XがX≧3L’となったビット列から同様にして3進数を抽出することができる。
【0227】
以上、2進数の一様乱数から3進数の一様乱数を効率的に生成する方法について説明した。
【0228】
<7:多変数多項式の係数を効率的に代入する方法について>
さて、これまでは多変数多項式を証明者(又は署名者)と検証者との間で共有する方法について具体的に明示してこなかった。多変数多項式を共有する方法としては、多変数多項式の係数(乱数)を生成する際に用いるシードを両者で共有する方法が考えられる。しかしながら、共有しているシードを利用して生成した乱数を係数に当てはめる順序を両者で共有しない限り、多変数多項式を共有したことにはならない。
【0229】
[7−1:基本的な取り決め]
そこで、証明者(又は署名者)と検証者との間で、共有しているシードを用いて生成した乱数列を、どの順序で多変数多項式に当てはめるかについて基本的な取り決めを行う。そして、多変数多項式を利用する際に、この基本的な取り決めに従って乱数列を多変数多項式に当てはめる。このような方法を用いれば、証明者(又は署名者)と検証者との間で多変数多項式を共有したことになる。
【0230】
[7−2:データの構造化]
但し、多変数多項式を構成する係数の数は膨大である。1つの係数が1ビット単位で表現されている場合、多変数多項式を表現するのに最低でも数万ビット以上のデータが必要になる。そのため、数を多変数多項式の係数に代入する処理の負荷は非常に高い。そこで、本件発明者は、多変数多項式の係数を所定の単位で構造化し、係数への代入処理を効率化する手法(構造化手法#1及び#2)を考案した。さらに、本件発明者は、同じ多変数多項式の係数に対して複数回の代入処理を実行する場合に、その処理効率を向上させる手法(構造化手法#3)を考案した。以下、これらの手法について詳細に説明する。
【0231】
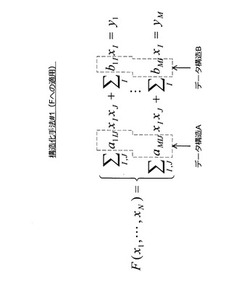
(7−2−1:構造化手法#1(図22〜図26))
まず、構造化手法#1について説明する。構造化手法#1は、図22及び図23に示すように、多変数多項式を構成する同じ種類の項の係数を1つのデータ構造として纏める手法である。図22の例では、多変数多項式Fの係数a1IJ〜aMIJがデータ構造Aとして纏められ、係数b1I〜bMIがデータ構造Bとして纏められている。また、図23に示すように、多変数多項式Gについても同様の手法が適用可能である。この場合、係数(a1IJ+a1JI)〜(aMIJ+aMJI)がデータ構造として纏められる。
【0232】
構造化手法#1を適用しない場合、M本のN変数多項式で構成される多変数多項式Fの計算は、(例1)に示すようなアルゴリズムにより行われる。(例1)の場合、1ビットのAND演算(&)を2×N×(N+1)×M/2回実行する必要がある。さらに、1ビットのXOR演算(^)を1×N×(N+1)×M/2回実行する必要がある。なお、入力xはNビットであるとする。
【0233】
(例1)
input x;
for L=1 to M
for I=1 to N
for J=I to N
[yのLビット目]^=[aLIJ]&[xのIビット目]&[xのJビット目];
end for
end for
end for
output y;
【0234】
一方、図22に示すように係数を構造化し、生成した乱数を多変数多項式Fの係数として一部ずつ逐次適用していく場合、係数の代入アルゴリズムは(例2)のようになる。(例2)の場合、MビットのAND演算(&)を2×N×(N+1)/2回、MビットのXOR演算(^)をN×(N+1)/2回実行するだけで済む。なお、a(1〜M)IJは、それぞれループのタイミングで生成される。また、係数を使い回してもよい。例えば、N(N−1)/2回のループを実行する際、[a(1〜M)IJ]を毎回生成せず、M回に1回だけ生成するようにしてもよい。また、M回のループ中、[a(1〜M)IJ]を1ビットずつローテーションしながら利用してもよい。
【0235】
(例2)
input x;
for I=1 to N
for J=I to N
[yの1〜Mビット目]^=[a(1〜M)IJ]&[xのIビット目]&[xのJビット目];
end for
end for
output y;
【0236】
また、図22に示すように係数を構造化する場合、多変数多項式Fの係数を適用した中間の結果をテーブルに保持するようにしてもよい。この場合、上記のアルゴリズムは(例3)のようになる。なお、配列aIJ[0][0]〜aIJ[2k−1][2k−1]には、それぞれ、aIJ[x1,…,xk][z1,…,zk]=(a(k(I−1)+1)(k(J−1)+1)&x1&z1)^…^(a(k(I−1)+1)(k(J−1)+k)&x1&zk)^…^(a(k(I−1)+k)(k(J−1)+1)&xk&z1)^…^(a(k(I−1)+k)(k(J−1)+k)&xk&zk)が格納されている。(例3)の場合、MビットのXOR演算(^)を(N/k)(N/k+1)/2回実行するだけで済む。但し、(例2)のアルゴリズムに比べると、必要なメモリ量は、22k/k2倍となる。
【0237】
例えば、k=1のとき、MビットXOR演算が120*119/2=7140回、必要なメモリ量が(例2)の22=4倍、ループ回数は変化なしとなる。また、k=2のとき、MビットXOR演算が60*59/2=1770回、必要なメモリ量が24/4=4倍、ループ回数が1/4となる。k=4のとき、MビットXOR演算が30*29/2=435回、必要なメモリ量が28/42=16倍、ループ回数が1/16.4となる。k=6のとき、MビットXOR演算が20*19/2=190回、必要なメモリ量が212/62=114倍、ループ回数が1/37.6となる。k=8のとき、MビットXOR演算が15*14/2=135回、必要なメモリが216/82=1024倍、ループ回数が1/52.9となる。
【0238】
(例3)
input x;
for I=1 to N/k
for J=I to N/k
[yの1〜Mビット目]^=a(1〜M)IJ[xのk(I−1)+1〜kビット目][xのk(J−1)+1〜kビット目];
end for
end for
output y;
【0239】
なお、(例3)に示した手法は、ちょうど、下記の式(33)で定義されるFIJ(…)の値を予め計算し、配列として保持しておく手法と言える。
【0240】
【数19】

【0241】
以上、構造化手法#1を多変数多項式Fへ適用するケースを例に挙げて具体的なアルゴリズムについて説明した。かかる構成により、アルゴリズムを実行する際に処理の高速化が期待できる。
【0242】
(Gへの適用)
ここまで、図22を参照しながら、構造化手法#1を適用して多変数多項式Fを計算するアルゴリズムについて説明してきた。一方で、多変数多項式Gの各要素も二次形式で表現されることから、図23に示すように、同様にして上記の構造化手法#1を多変数多項式Gの計算にそのまま適用することも可能である。
【0243】
例えば、上記の構造化手法#1を適用しない場合、多変数多項式Gを計算するアルゴリズムは、下記の(例1’)のように表現される。なお、入力x及びyはそれぞれNビットであるとする。
【0244】
(例1’)
input x,y;
for L=1 to M
for I=1 to N
for J=1 to N
[zのLビット目]^=[aLIJ+aLJI]&[xのIビット目]&[yのJビット目];
end for
end for
end for
output z;
【0245】
上記の(例1’)に対し、上述した構造化手法#1を適用すると、多変数多項式Gを計算するアルゴリズムは、下記の(例2’)のようになる。
【0246】
(例2’)
input x,y;
for I=1 to N
for J=1 to N
[zの1〜Mビット目]^=[a(1〜M)IJ+a(1〜M)JI]&[xのIビット目]&[yのJビット目];
end for
end for
output z;
【0247】
また、多変数多項式Gの係数を適用した中間の結果をテーブルに保持する手法の場合、多変数多項式Gを計算するアルゴリズムは、上記の(例3)に対応して下記の(例3’)のようになる。なお、配列aIJ[0][0]〜aIJ[2k−1][2k−1]には、それぞれ、aIJ[x1,…,xk][y1,…,yk]=(a(k(I−1)+1)(k(J−1)+1)&x1&y1)^…^(a(k(I−1)+1)(k(J−1)+k)&x1&yk)^…^(a(k(I−1)+k)(k(J−1)+1)&xk&y1)^…^(a(k(I−1)+k)(k(J−1)+k)&xk&yk)が格納されている。
【0248】
(例3’)の場合、MビットのXOR演算(^)を(N/k)2回実行するだけで済む。但し、(例2’)のアルゴリズムに比べると、必要なメモリ量は、22k/k2倍となる。
【0249】
例えば、k=1のとき、MビットXOR演算が1202=14400回、必要なメモリ量が(例2’)の22=4倍、ループ回数は変化なしとなる。また、k=2のとき、MビットXOR演算が602=3600回、必要なメモリ量が24/4=4倍、ループ回数が1/4となる。k=4のとき、MビットXOR演算が302=900回、必要なメモリ量が28/42=16倍、ループ回数が1/16となる。k=6のとき、MビットXOR演算が202=400回、必要なメモリ量が212/62=114倍、ループ回数が1/36となる。k=8のとき、MビットXOR演算が152=225回、必要なメモリが216/82=1024倍、ループ回数が1/64となる。
【0250】
(例3’)
input x,y;
for I=1 to N/k
for J=I to N/k
[zの1〜Mビット目]^=a(1〜M)IJ[xのk(I−1)+1〜kビット目][yのk(J−1)+1〜kビット目];
end for
end for
output z;
【0251】
なお、(例3’)に示した手法は、ちょうど、下記の式(34)で定義されるGIJ(…)の値を予め計算し、配列として保持しておく手法と言える。
【0252】
【数20】

【0253】
以上、多変数多項式Gを計算するケースを例に挙げ、構造化手法#1に係る具体的なアルゴリズムの構成について説明した。かかる構成により、アルゴリズムを実行する際に処理の高速化が期待できる。
【0254】
(3次多変数多項式Fへの適用)
ここまで、構造化手法#1の具体例として、2次の多変数多項式の係数を構造化する手法を紹介してきたが、同様にして3次の多変数多項式の係数を構造化することも可能である。図24の例では、係数a1IJL〜aMIJLがデータ構造Aとして纏められ、係数b1IJ〜bMIJがデータ構造Bとして纏められ、係数c1I〜cMIがデータ構造Cとして纏められる。このように係数を構造化することで多変数多項式の計算が効率化される。
【0255】
例えば、データ構造Aに係る計算について具体的に考えてみたい。係数を構造化しない場合、当該データ構造Aに係る計算のアルゴリズムは、例えば、下記(例4)のようになる。
【0256】
(例4)
input x;
for Q=I to M
for I=1 to N
for J=I to N
for L=J to N
[yのQビット目]^=[aQIJL]&[xのIビット目]&[xのJビット目]&[xのLビット目];
end for
end for
end for
end for
output y;
【0257】
一方、係数を構造化すると、下記(例5)のようなアルゴリズムとなる。(例5)の場合、MビットのAND演算(&)を2×N×(N+1)×(N+2)/6回、MビットのXOR演算(^)を1×N×(N+1)×(N+2)/6回実行するだけで済む。なお、a(1〜M)IJLは、それぞれループのタイミングで生成される。また、係数を使い回してもよい。例えば、ループを実行する際、[a(1〜M)IJL]を毎回生成せず、M回に1回だけ生成するようにしてもよい。また、M回のループ中、[a(1〜M)IJ]を1ビットずつローテーションしながら利用してもよい。
【0258】
(例5)
input x;
for I=1 to N
for J=I to N
for L=J to N
[yの1〜Mビット目]^=[a(1〜M)IJL]&[xのIビット目]&[xのJビット目]&[xのLビット目];
end for
end for
output y;
【0259】
また、係数を構造化する場合、多変数多項式Fの係数を適用した中間の結果をテーブルに保持するようにしてもよい。この場合、上記のアルゴリズムは(例6)のようになる。なお、配列aIJL[0][0][0]〜aIJL[2k−1][2k−1][2k−1]には、それぞれ、aIJL[x1,…,xk][z1,…,zk][w1,…,wk]=Σ1≦α,β,γ≦k(a(k(I−1)+α)(k(J−1)+β)(k(L−1)+γ)&xα&zβ&wγ)が格納されている。(例6)の場合、MビットのXOR演算(^)を(N/k)(N/k+1)(N/k+2)/6回実行するだけで済む。但し、(例4)のアルゴリズムに比べると、必要なメモリ量は、23k/k3倍となる。
【0260】
例えば、k=1のとき、MビットXOR演算が120*121*122/6=295240回、必要なメモリ量が(例4)の23=8倍、ループ回数は変化なしとなる。また、k=2のとき、MビットXOR演算が60*61*62/6=37820回、必要なメモリ量が26/8=8倍、ループ回数が1/7.8となる。k=4のとき、MビットXOR演算が30*31*32/6=4960回、必要なメモリ量が212/43=64倍、ループ回数が1/59.5となる。k=6のとき、MビットXOR演算が20*21*22/6=1540回、必要なメモリ量が218/63=1214倍、ループ回数が1/192となる。
【0261】
(例6)
input x;
for I=1 to N/k
for J=I to N/k
for L=J to N/k
[yの1〜Mビット目]^=a(1〜M)IJL[xのk(I−1)+1〜kビット目][xのk(J−1)+1〜kビット目][xのk(L−1)+1〜kビット目];
end for
end for
end for
output y;
【0262】
なお、(例6)に示した手法は、ちょうど、下記の式(35)で定義されるFIJ(…)の値を予め計算し、配列として保持しておく手法と言える。
【0263】
【数21】

【0264】
以上、構造化手法#1を3次の多変数多項式Fへ適用するケースについて説明した。かかる構成により、アルゴリズムを実行する際に処理の高速化が期待できる。
【0265】
(3次多変数多項式Gx,Gyへの適用)
上記の(例5)や(例6)と同様、図25及び図26に示すように、3次の多変数多項式Gx,Gyに対しても構造化手法#1を適用することが可能である。構造化手法#1を適用しない場合、3次の多変数多項式Gxのデータ構造Aに係る計算は、例えば、下記の(例4’X)のアルゴリズムにより実行される。
【0266】
(例4’X)
input x,y;
for Q=1 to M
for I=1 to N
for J=1 to N
for L=1 to N
[zのQビット目]^=[aQIJL+aQILJ+aQLJI]&[yのIビット目]&[yのJビット目]&[xのLビット目];
end for
end for
end for
end for
output z;
【0267】
上記の(例4’X)に対し、上述した構造化手法#1を適用すると、多変数多項式Gxを計算するアルゴリズムは、下記の(例5’X)のようになる。また、上記の(例6)と同様にして多変数多項式Gxの係数を適用した中間の結果をテーブルに保持するようにしてもよい。
【0268】
(例5’X)
input x,y;
for I=1 to N
for J=1 to N
for L=1 to N
[zの1〜Mビット目]^=[a(1〜M)IJL+a(1〜M)ILJ+a(1〜M)LJI]&[yのIビット目]&[yのJビット目]&[xのLビット目];
end for
end for
end for
output z;
【0269】
また、構造化手法#1を適用しない場合、3次の多変数多項式Gyの計算は、例えば、下記の(例4’Y)のアルゴリズムにより実行される。
【0270】
(例4’Y)
input x,y;
for Q=1 to M
for I=1 to N
for J=1 to N
for L=1 to N
[zのQビット目]^=[aQIJL+aQILJ+aQLJI]&[xのIビット目]&[xのJビット目]&[yのLビット目];
end for
end for
end for
end for
output z;
【0271】
上記の(例4’Y)に対し、上述した構造化手法#1を適用すると、多変数多項式Gyを計算するアルゴリズムは、下記の(例5’Y)のようになる。また、上記の(例6)と同様にして多変数多項式Gyの係数を適用した中間の結果をテーブルに保持するようにしてもよい。
【0272】
(例5’Y)
input x,y;
for I=1 to N
for J=1 to N
for L=1 to N
[zの1〜Mビット目]^=[a(1〜M)IJL+a(1〜M)ILJ+a(1〜M)LJI]&[xのIビット目]&[xのJビット目]&[yのLビット目];
end for
end for
end for
output z;
【0273】
以上、構造化手法#1を3次の多変数多項式Gx、Gyへ適用するケースについて説明した。かかる構成により、アルゴリズムを実行する際に処理の高速化が期待できる。
【0274】
(7−2−2:構造化手法#2(図27))
次に、構造化手法#2について説明する。構造化手法#2は、図27に示すように、多変数多項式を2次形式で表現し、2次形式の行又は列を1つのデータ構造として纏める手法である。図27の例では、行方向にデータ構造が纏められている。
【0275】
図27に示すように係数を構造化し、生成した乱数を多変数多項式の係数として一部ずつ逐次適用していく場合、係数の代入アルゴリズムは(例4)のようになる。例4の場合、NビットのAND演算(&)を(N+1)×M回、NビットのXOR演算(^)をN×M回、関数Qの演算をM回実行するだけで済む。
【0276】
(例4)
for I=1 to N
T^=AI&[xのIビット目];
end for
T&=x;
output Q(T);
【0277】
Q(z){
z=z^(z>>1);
z=z^(z>>2);
z=z^(z>>4);
z=z^(z>>8);
・・・
z=z^(z>>2Log(N));
return z&1;
}
【0278】
また、図27に示すように係数を構造化し、多変数多項式の係数を適用した中間の結果をテーブルに保持するようにしてもよい。この場合、係数の代入アルゴリズムは(例5)のようになる。なお、配列AI[0]〜AI[2k−1]には、それぞれ、AI[x1,…,xk]=(A(k(I−1)+1)&x1)^…^(A(k(I−1)+k)&xk)が格納されている。例5の場合、NビットのXOR演算(^)を(N/k)×M、Nビットの関数Qの演算をM回実行するだけで済む。但し、(例4)のアルゴリズムに比べると、必要なメモリ量は、2k/k倍となる。
【0279】
例えば、k=1のとき、NビットXOR演算が120回、必要なメモリ量が(例4)の2倍、ループ回数は変化なしとなる。また、k=4のとき、NビットXOR演算が30回、必要なメモリ量が24/4=4倍、ループ回数が1/4となる。k=8のとき、NビットXOR演算が15回、必要なメモリが28/8=32倍、ループ回数が1/8となる。k=16のとき、NビットXOR演算が8回、必要なメモリが216/16=4096倍、ループ回数が1/15となる。
【0280】
(例5)
for I=1 to N/k
T^=AI[xのk(I−1)+1〜k(I−1)+kビット目];
end for
T&=x;
output Q(T);
【0281】
以上、構造化手法#2に係る具体的な係数の代入アルゴリズムについて説明した。かかる構成により、アルゴリズムを実行する際に処理の高速化が期待できる。
【0282】
(7−2−3:構造化手法#3)
次に、構造化手法#3について説明する。構造化手法#3は、同じ多変数多項式にN回(N≧2)代入処理を行なう場合に、乱数から多項式をN回生成して代入処理を行うのではなく、「係数を一部生成し、その部分に関するN回分の処理を行なう」部分を単位とする逐次的な処理をN回分並列して行なうという手法である。この手法を適用すると、乱数生成のコストが無視できない場合にN回分の処理全体でのスループットが改善される。
【0283】
例えば、図5に示したアルゴリズムでは、工程#1において引数を更新しながら多変数多項式F及びGの計算をN回繰り返し実行している。そこで、このような計算部分について、同じ係数を利用して繰り返し演算を行うように構成する。上記(例2)のアルゴリズムを用いて多変数多項式F(r0i)(i=1〜N)を計算する場合、一度生成した[aIJL]について、N個のr0iを全て適用した後で、次の[aIJL]に関する処理を実行するように構成する。このように構成すると、同じ係数[aIJL]をN回生成せずに済むようになる。
【0284】
以上、構造化手法#3に係る具体的な係数の代入アルゴリズムについて説明した。かかる構成により、N回分の処理におけるトータルでのスループットが改善される。
【0285】
<8:ハードウェア構成例(図28)>
上記の各アルゴリズムは、例えば、図28に示す情報処理装置のハードウェア構成を用いて実行することが可能である。つまり、当該各アルゴリズムの処理は、コンピュータプログラムを用いて図28に示すハードウェアを制御することにより実現される。なお、このハードウェアの形態は任意であり、例えば、パーソナルコンピュータ、携帯電話、PHS、PDA等の携帯情報端末、ゲーム機、接触式又は非接触式のICチップ、接触式又は非接触式のICカード、又は種々の情報家電がこれに含まれる。但し、上記のPHSは、Personal Handy−phone Systemの略である。また、上記のPDAは、Personal Digital Assistantの略である。
【0286】
図28に示すように、このハードウェアは、主に、CPU902と、ROM904と、RAM906と、ホストバス908と、ブリッジ910と、を有する。さらに、このハードウェアは、外部バス912と、インターフェース914と、入力部916と、出力部918と、記憶部920と、ドライブ922と、接続ポート924と、通信部926と、を有する。但し、上記のCPUは、Central Processing Unitの略である。また、上記のROMは、Read Only Memoryの略である。そして、上記のRAMは、Random Access Memoryの略である。
【0287】
CPU902は、例えば、演算処理装置又は制御装置として機能し、ROM904、RAM906、記憶部920、又はリムーバブル記録媒体928に記録された各種プログラムに基づいて各構成要素の動作全般又はその一部を制御する。ROM904は、CPU902に読み込まれるプログラムや演算に用いるデータ等を格納する手段である。RAM906には、例えば、CPU902に読み込まれるプログラムや、そのプログラムを実行する際に適宜変化する各種パラメータ等が一時的又は永続的に格納される。
【0288】
これらの構成要素は、例えば、高速なデータ伝送が可能なホストバス908を介して相互に接続される。一方、ホストバス908は、例えば、ブリッジ910を介して比較的データ伝送速度が低速な外部バス912に接続される。また、入力部916としては、例えば、マウス、キーボード、タッチパネル、ボタン、スイッチ、及びレバー等が用いられる。さらに、入力部916としては、赤外線やその他の電波を利用して制御信号を送信することが可能なリモートコントローラ(以下、リモコン)が用いられることもある。
【0289】
出力部918としては、例えば、CRT、LCD、PDP、又はELD等のディスプレイ装置、スピーカ、ヘッドホン等のオーディオ出力装置、プリンタ、携帯電話、又はファクシミリ等、取得した情報を利用者に対して視覚的又は聴覚的に通知することが可能な装置である。但し、上記のCRTは、Cathode Ray Tubeの略である。また、上記のLCDは、Liquid Crystal Displayの略である。そして、上記のPDPは、Plasma DisplayPanelの略である。さらに、上記のELDは、Electro−Luminescence Displayの略である。
【0290】
記憶部920は、各種のデータを格納するための装置である。記憶部920としては、例えば、ハードディスクドライブ(HDD)等の磁気記憶デバイス、半導体記憶デバイス、光記憶デバイス、又は光磁気記憶デバイス等が用いられる。但し、上記のHDDは、Hard Disk Driveの略である。
【0291】
ドライブ922は、例えば、磁気ディスク、光ディスク、光磁気ディスク、又は半導体メモリ等のリムーバブル記録媒体928に記録された情報を読み出し、又はリムーバブル記録媒体928に情報を書き込む装置である。リムーバブル記録媒体928は、例えば、DVDメディア、Blu−rayメディア、HD DVDメディア、各種の半導体記憶メディア等である。もちろん、リムーバブル記録媒体928は、例えば、非接触型ICチップを搭載したICカード、又は電子機器等であってもよい。但し、上記のICは、Integrated Circuitの略である。
【0292】
接続ポート924は、例えば、USBポート、IEEE1394ポート、SCSI、RS−232Cポート、又は光オーディオ端子等のような外部接続機器930を接続するためのポートである。外部接続機器930は、例えば、プリンタ、携帯音楽プレーヤ、デジタルカメラ、デジタルビデオカメラ、又はICレコーダ等である。但し、上記のUSBは、Universal Serial Busの略である。また、上記のSCSIは、Small Computer System Interfaceの略である。
【0293】
通信部926は、ネットワーク932に接続するための通信デバイスであり、例えば、有線又は無線LAN、Bluetooth(登録商標)、又はWUSB用の通信カード、光通信用のルータ、ADSL用のルータ、又は接触又は非接触通信用のデバイス等である。また、通信部926に接続されるネットワーク932は、有線又は無線により接続されたネットワークにより構成され、例えば、インターネット、家庭内LAN、赤外線通信、可視光通信、放送、又は衛星通信等である。但し、上記のLANは、Local Area Networkの略である。また、上記のWUSBは、Wireless USBの略である。そして、上記のADSLは、Asymmetric Digital Subscriber Lineの略である。
【0294】
<9:まとめ>
最後に、本技術の実施形態に係る技術内容について簡単に纏める。ここで述べる技術内容は、例えば、PC、携帯電話、ゲーム機、情報端末、情報家電、カーナビゲーションシステム等、種々の情報処理装置に対して適用することができる。なお、以下で述べる情報処理装置の機能は、1台の情報処理装置を利用して実現することも可能であるし、複数台の情報処理装置を利用して実現することも可能である。また、以下で述べる情報処理装置が処理を実行する際に用いるデータ記憶手段及び演算処理手段は、当該情報処理装置に設けられたものであってもよいし、ネットワークを介して接続された機器に設けられたものであってもよい。
【0295】
上記の情報処理装置の機能構成は以下のように表現される。例えば、下記(1)に記載の情報処理装置は、多次多変数連立方程式の求解困難性に安全性の根拠を置く効率的な公開鍵認証方式又は電子署名方式のアルゴリズムを実行する機能を有する。
【0296】
(1)
多次多変数多項式の組F=(f1,…,fm)を含む公開鍵を利用した公開鍵認証方式又は電子署名方式のアルゴリズムを実行するエンティティの間で共有されている情報から所定の関数を用いて、前記多次多変数多項式の組Fを構成する各項の係数に利用する数を生成する数生成部と、
前記数生成部が生成した数を、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式の係数に割り当てる割当部と、
を備え、
前記割当部は、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式の係数のうち、変数の組み合わせの種類が同じ項の係数をグループ化しておき、割り当て処理をグループ単位で実行する、
情報処理装置。
【0297】
(2)
多次多変数多項式の組F=(f1,…,fm)を含む公開鍵を利用した公開鍵認証方式又は電子署名方式のアルゴリズムを実行するエンティティの間で共有されている情報から所定の関数を用いて、前記多次多変数多項式の組Fを構成する各項の係数に利用する数を生成する数生成部と、
前記数生成部が生成した数を、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式の係数に割り当てる割当部と、
を備え、
前記割当部は、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式を2次形式で表現した場合の係数行列を行又は列毎にグループ化しておき、割り当て処理をグループ単位で実行する、
情報処理装置。
【0298】
(3)
前記数生成部は、前記割当部が1つのグループに対する割り当て処理を実行する際に、当該1つのグループに属する係数の分だけ前記数を生成する、
上記(1)又は(2)に記載の情報処理装置。
【0299】
(4)
前記数生成部は、前記1つのグループに属する係数の分だけ前記数を生成する際、1つの数を生成し、生成した数を1ビットずつローテーションして所要数の数を生成する、
上記(3)に記載の情報処理装置。
【0300】
(5)
前記各グループに対応する種類の項に前記係数を割り当て、当該項の変数に任意の数を代入した値をテーブルとして保持するテーブル保持部をさらに備える、
上記(1)又は(2)に記載の情報処理装置。
【0301】
(6)
多次多変数多項式の組F=(f1,…,fm)を含む公開鍵を利用した公開鍵認証方式又は電子署名方式のアルゴリズムを実行するエンティティの間で共有されている情報から所定の関数を用いて前記多次多変数多項式の組Fを構成する各項の係数と同じ数だけ数を生成する数生成部と、
前記証明者と前記認証者との間で予め決められた順序で前記数生成部が生成した数を、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式の係数に割り当てる割当部と、
を備える、
情報処理装置。
【0302】
(7)
前記情報は、乱数のシードであり、
前記所定の関数は、前記シードを利用して乱数を生成する乱数生成器である、
上記(1)〜(6)のいずれか1項に記載の情報処理装置。
【0303】
(8)
環K上で定義される多次多変数多項式の組F=(f1,…,fm)、及びベクトルs∈Knに基づいてメッセージを生成するメッセージ生成部と、
前記多次多変数多項式の組F及びベクトルy=(y1,…,ym)=(f1(s),…,fm(s))を保持する検証者に前記メッセージを提供するメッセージ提供部と、
k通り(k≧3)の検証パターンの中から前記検証者が選択した検証パターンに対応する回答情報を前記検証者に提供する回答提供部と、
を備え、
前記ベクトルsは秘密鍵であり、
前記多次多変数多項式の組F及び前記ベクトルyは公開鍵であり、
前記回答情報は、前記乱数の組及び前記メッセージの中から前記検証パターンに応じて選択される情報であり、
前記メッセージは、前記公開鍵及び前記回答情報を利用して、当該回答情報に対応する検証パターン用に予め用意された演算を実行することで得られる情報である、
上記(1)〜(7)のいずれか1項に記載の情報処理装置。
【0304】
(9)
環K上で定義される多次多変数多項式の組F=(f1,…,fm)及びベクトルy=(y1,…,ym)=(f1(s),…,fm(s))を保持する情報保持部と、
前記多次多変数多項式の組F及びベクトルs∈Knに基づいて生成されたメッセージを取得するメッセージ取得部と、
前記メッセージを提供した証明者に対し、k通り(k≧3)の検証パターンの中からランダムに選択した1つの検証パターンの情報を提供するパターン情報提供部と、
前記選択した検証パターンに対応する回答情報を前記証明者から取得する回答取得部と、
前記メッセージ、前記多次多変数多項式の組F、前記ベクトルy、及び前記回答情報に基づいて前記証明者が前記ベクトルsを保持しているか否かを検証する検証部と、
を備え、
前記ベクトルsは秘密鍵であり、
前記多次多変数多項式の組F及び前記ベクトルyは公開鍵であり、
前記メッセージは、前記公開鍵及び前記回答情報を利用して、当該回答情報に対応する検証パターン用に予め用意された演算を実行することで得られる情報である、
上記(1)〜(7)のいずれか1項に記載の情報処理装置。
【0305】
(10)
環K上で定義される多次多変数多項式の組F=(f1,…,fm)、及びベクトルs∈Knに基づいてメッセージを生成するメッセージ生成部と、
前記多次多変数多項式の組F及びベクトルy=(y1,…,ym)=(f1(s),…,fm(s))を保持する検証者に前記メッセージを提供するメッセージ提供部と、
前記検証者がランダムに選択した第1の情報及び前記メッセージを生成する際に得られる第2の情報を用いて第3の情報を生成する中間情報生成部と、
前記検証者に前記第3の情報を提供する中間情報提供部と、
k通り(k≧2)の検証パターンの中から前記検証者が選択した検証パターンに対応する回答情報を前記検証者に提供する回答提供部と、
を備え、
前記ベクトルsは秘密鍵であり、
前記多次多変数多項式の組F及び前記ベクトルyは公開鍵であり、
前記回答情報は、前記メッセージの中から前記検証パターンに応じて選択される情報であり、
前記メッセージは、前記公開鍵、前記第1の情報、前記第3の情報、前記回答情報を利用して、当該回答情報に対応する検証パターン用に予め用意された演算を実行することで得られる情報である、
上記(1)〜(7)のいずれか1項に記載の情報処理装置。
【0306】
(11)
環K上で定義される多次多変数多項式の組F=(f1,…,fm)及びベクトルy=(y1,…,ym)=(f1(s),…,fm(s))を保持する情報保持部と、
前記多次多変数多項式の組F及びベクトルs∈Knに基づいて生成されたメッセージを取得するメッセージ取得部と、
前記メッセージを提供した証明者に対し、ランダムに選択した第1の情報を提供する情報提供部と、
前記第1の情報及び前記メッセージを生成する際に得られる第2の情報を用いて前記証明者が生成した第3の情報を取得する中間情報取得部と、
k通り(k≧3)の検証パターンの中からランダムに選択した1つの検証パターンの情報を前記証明者に提供するパターン情報提供部と、
前記選択した検証パターンに対応する回答情報を前記証明者から取得する回答取得部と、
前記メッセージ、前記第1の情報、前記第3の情報、前記多次多変数多項式の組F、及び前記回答情報に基づいて前記証明者が前記ベクトルsを保持しているか否かを検証する検証部と、
を備え、
前記ベクトルsは秘密鍵であり、
前記多次多変数多項式の組F及び前記ベクトルyは公開鍵であり、
前記メッセージは、前記公開鍵、前記第1の情報、前記第3の情報、前記回答情報を利用して当該回答情報に対応する検証パターン用に予め用意された演算を実行することで得られる情報である、
上記(1)〜(7)のいずれか1項に記載の情報処理装置。
【0307】
(12)
前記アルゴリズムが複数回繰り返し実行される場合において、前記数生成部は1回だけ前記数を生成し、前記割当部は1回だけ前記割り当て処理を実行し、
前記アルゴリズムは、前記割当部が割り当てた係数を繰り返し利用する、
上記(1)又は(2)に記載の情報処理装置。
【0308】
(13)
環K上で定義される多次多変数多項式の組F=(f1,…,fm)、及び署名鍵s∈Knを用いて文書Mに対する電子署名を生成する署名生成部と、
前記多次多変数多項式の組F及びベクトルy=(f1(s),…,fm(s))を保持する検証者へと前記電子署名を提供する署名提供部と、
を備える、
上記(1)〜(7)のいずれか1項に記載の情報処理装置。
【0309】
(14)
多次多変数多項式の組F=(f1,…,fm)を含む公開鍵を利用した公開鍵認証方式又は電子署名方式のアルゴリズムを実行するエンティティの間で共有されている情報から所定の関数を用いて、前記多次多変数多項式の組Fを構成する各項の係数に利用する数を生成するステップと、
生成した数を、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式の係数に割り当てるステップと、
を含み、
前記割り当てるステップでは、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式の係数のうち、変数の組み合わせの種類が同じ項の係数をグループ化しておき、割り当て処理をグループ単位で実行する、
情報処理方法。
【0310】
(15)
多次多変数多項式の組F=(f1,…,fm)を含む公開鍵を利用した公開鍵認証方式又は電子署名方式のアルゴリズムを実行するエンティティの間で共有されている情報から所定の関数を用いて、前記多次多変数多項式の組Fを構成する各項の係数に利用する数を生成するステップと、
生成した数を、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式の係数に割り当てるステップと、
を含み、
前記割り当てるステップでは、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式を2次形式で表現した場合の係数行列を行又は列毎にグループ化しておき、割り当て処理をグループ単位で実行する、
情報処理方法。
【0311】
(16)
多次多変数多項式の組F=(f1,…,fm)を含む公開鍵を利用した公開鍵認証方式又は電子署名方式のアルゴリズムを実行するエンティティの間で共有されている情報から所定の関数を用いて前記多次多変数多項式の組Fを構成する各項の係数と同じ数だけ数を生成するステップと、
前記証明者と前記認証者との間で予め決められた順序で前記数生成部が生成した数を、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式の係数に割り当てるステップと、
を含む、
情報処理方法。
【0312】
(17)
多次多変数多項式の組F=(f1,…,fm)を含む公開鍵を利用した公開鍵認証方式又は電子署名方式のアルゴリズムを実行するエンティティの間で共有されている情報から所定の関数を用いて、前記多次多変数多項式の組Fを構成する各項の係数に利用する数を生成する数生成機能と、
前記数生成機能が生成した数を、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式の係数に割り当てる割当機能と、
をコンピュータに実現させるためのプログラムであり、
前記割当機能は、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式の係数のうち、変数の組み合わせの種類が同じ項の係数をグループ化しておき、割り当て処理をグループ単位で実行する、
プログラム。
【0313】
(18)
多次多変数多項式の組F=(f1,…,fm)を含む公開鍵を利用した公開鍵認証方式又は電子署名方式のアルゴリズムを実行するエンティティの間で共有されている情報から所定の関数を用いて、前記多次多変数多項式の組Fを構成する各項の係数に利用する数を生成する数生成機能と、
前記数生成機能が生成した数を、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式の係数に割り当てる割当機能と、
をコンピュータに実現させるためのプログラムであり、
前記割当機能は、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式を2次形式で表現した場合の係数行列を行又は列毎にグループ化しておき、割り当て処理をグループ単位で実行する、
プログラム。
【0314】
(19)
多次多変数多項式の組F=(f1,…,fm)を含む公開鍵を利用した公開鍵認証方式又は電子署名方式のアルゴリズムを実行するエンティティの間で共有されている情報から所定の関数を用いて前記多次多変数多項式の組Fを構成する各項の係数と同じ数だけ数を生成する数生成機能と、
前記証明者と前記認証者との間で予め決められた順序で前記数生成部が生成した数を、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式の係数に割り当てる割当機能と、
をコンピュータに実現させるためのプログラム。
【0315】
(20)
上記の(19)に記載のプログラムが記録された、コンピュータにより読み取り可能な記録媒体。
【0316】
(備考)
上記の証明者アルゴリズムP、検証者アルゴリズムV、署名生成アルゴリズムSig、署名検証アルゴリズムVerは、数生成部、割当部、テーブル保持部の一例である。上記の証明者アルゴリズムPは、メッセージ生成部、メッセージ提供部、回答提供部、中間情報生成部、中間情報提供部の一例である。また、上記の検証者アルゴリズムVは、情報保持部、メッセージ取得部、パターン情報提供部、回答取得部、検証部、中間情報取得部の一例である。
【0317】
以上、添付図面を参照しながら本技術の好適な実施形態について説明したが、本技術は係る例に限定されないことは言うまでもない。当業者であれば、特許請求の範囲に記載された範疇内において、各種の変更例または修正例に想到し得ることは明らかであり、それらについても当然に本技術の技術的範囲に属するものと了解される。
【0318】
上記の説明において、ハッシュ関数Hを用いるアルゴリズムを紹介したが、ハッシュ関数Hの代わりにコミットメント関数COMを用いてもよい。コミットメント関数COMは、文字列S及び乱数ρを引数にとる関数である。コミットメント関数の例としては、Shai HaleviとSilvio Micaliによって国際会議CRYPTO1996で発表された方式などがある。
【符号の説明】
【0319】
Gen 鍵生成アルゴリズム
P 証明者アルゴリズム
V 検証者アルゴリズム
Sig 署名生成アルゴリズム
Ver 署名検証アルゴリズム
【技術分野】
【0001】
本技術は、情報処理装置、情報処理方法、及びプログラムに関する。
【背景技術】
【0002】
情報処理技術や通信技術の急速な発展に伴い、公文書、私文書を問わず、文書の電子化が急速に進んでいる。これに伴い、多くの個人や企業は、電子文書の安全管理に大きな関心を寄せている。こうした関心の高まりを受け、各方面で電子文書の盗聴や偽造等のタンパリング行為に対する対抗策が盛んに研究されるようになってきた。電子文書の盗聴に対しては、例えば、電子文書を暗号化することにより安全性が確保される。また、電子文書の偽造に対しては、例えば、電子署名を利用することにより安全性が確保される。但し、利用する暗号や電子署名が高いタンパリング耐性を有していなければ、十分な安全性が保証されない。
【0003】
電子署名は、電子文書の作成者を特定するために利用される。そのため、電子署名は、電子文書の作成者しか生成できないようにすべきである。仮に、悪意ある第三者が同じ電子署名を生成できてしまうと、その第三者が電子文書の作成者に成りすますことができてしまう。つまり、悪意ある第三者により電子文書が偽造されてしまう。こうした偽造を防止するため、電子署名の安全性については様々な議論が交わされてきた。現在広く利用されている電子署名方式としては、例えば、RSA署名方式やDSA署名方式などが知られている。
【0004】
RSA署名方式は、「大きな合成数に対する素因数分解の困難性(以下、素因数分解問題)」を安全性の根拠とする。また、DSA署名方式は、「離散対数問題に対する解の導出の困難性」を安全性の根拠とする。これらの根拠は、古典的なコンピュータを利用して素因数分解問題や離散対数問題を効率的に解くアルゴリズムが存在しないことに起因する。つまり、上記の困難性は、古典的なコンピュータにおける計算量的な困難性を意味する。しかしながら、量子コンピュータを用いると、素因数分解問題や離散対数問題に対する解答が効率的に算出されてしまうと言われている。
【0005】
現在利用されている電子署名方式や公開鍵認証方式の多くは、RSA署名方式やDSA署名方式と同様、素因数分解問題や離散対数問題の困難性に安全性の根拠をおいている。そのため、こうした電子署名方式や公開鍵認証方式は、量子コンピュータが実用化された場合に、その安全性が確保されないことになる。そこで、素因数分解問題や離散対数問題など、量子コンピュータにより容易に解かれてしまう問題とは異なる問題に安全性の根拠をおく新たな電子署名方式及び公開鍵認証方式の実現が求められている。量子コンピュータにより容易に解くことが難しい問題としては、例えば、多変数多項式問題がある。
【0006】
多変数多項式問題に安全性の根拠をおく電子署名方式としては、例えば、MI(Matsumoto−Imai cryptography)、HFE(Hidden Field Equation cryptography)、OV(Oil−Vinegar signature scheme)、TTM(Tamed Transformation Method cryptography)に基づく方式が知られている。例えば、下記の非特許文献1、2には、HFEに基づく電子署名方式が開示されている。
【先行技術文献】
【非特許文献】
【0007】
【非特許文献1】Jacques Patarin Asymmetric Cryptography with a Hidden Monomial. CRYPTO 1996, pp.45−60.
【非特許文献2】Patarin, J., Courtois, N., and Goubin, L. QUARTZ, 128−Bit Long Digital Signatures. In Naccache,D., Ed. Topics in Cryptology − CT−RSA 2001 (San Francisco, CA, USA, April 2001), vol. 2020 of Lecture Notes in Computer Science, Springer−Verlag., pp.282−297.
【発明の概要】
【発明が解決しようとする課題】
【0008】
上記の通り、多変数多項式問題は、量子コンピュータを用いても解くことが困難なNP困難問題と呼ばれる問題の一例である。通常、HFEなどに代表される多変数多項式問題を利用した公開鍵認証方式は、特殊なトラップドアが仕込まれた多次多変数連立方程式を利用している。例えば、x1,…,xnに関する多次多変数連立方程式F(x1,…,xn)=yと線形変換A及びBが用意され、線形変換A及びBが秘密に管理される。この場合、多次多変数連立方程式F、線形変換A及びBがトラップドアとなる。
【0009】
トラップドアF,A,Bを知っているエンティティは、x1,…,xnに関する方程式B(F(A(x1,…,xn)))=y’を解くことができる。一方、トラップドアF,A,Bを知らないエンティティは、x1,…,xnに関する方程式B(F(A(x1,…,xn)))=y’を解くことができない。この仕組みを利用することにより、多次多変数連立方程式の解答困難性を安全性の根拠とする公開鍵認証方式や電子署名方式が実現される。
【0010】
上記の通り、こうした公開鍵認証方式や電子署名方式を実現するには、B(F(A(x1,…,xn)))=yを満たすような特殊な多次多変数連立方程式を用意する必要がある。また、署名生成時に多次多変数連立方程式Fを解く必要がある。そのため、利用可能な多次多変数連立方程式Fは、比較的容易に解けるものに限られていた。すなわち、これまでの方式においては、比較的容易に解ける3つの関数(トラップドア)B、F、Aを合成した形の多次多変数連立方程式B(F(A(x1,…,xn)))=yしか用いることができず、十分な安全性を確保することが難しかった。
【0011】
そこで、本件発明者は、上記の事情に鑑みて、効率的に解く手段(トラップドア)が知られていない多次多変数連立方程式を用いて高い安全性を有する効率的な公開鍵認証方式及び電子署名方式を考案した(Koichi Sakumoto,Taizo Shirai and Harunaga Hiwatari,“Public−Key Identification Schemes Based on Multivariate Quadratic Polynomials”,CRYPTO 2011,LNCS 6841,pp.706−723,2011.)。
【0012】
しかし、この公開鍵認証方式及び電子署名方式で利用する多変数多項式は係数の数が多く、公開鍵として利用するには、証明者と検証者との間で効率的に係数を割り当てる方法を決めておく必要があった。本技術は、効率的に多変数多項式の係数を代入することが可能な、新規かつ改良された情報処理装置、情報処理方法、及びプログラムの提供を意図して考案されたものである。
【課題を解決するための手段】
【0013】
本技術のある観点によれば、多次多変数多項式の組F=(f1,…,fm)を含む公開鍵を利用した公開鍵認証方式又は電子署名方式のアルゴリズムを実行するエンティティの間で共有されている情報から所定の関数を用いて、前記多次多変数多項式の組Fを構成する各項の係数に利用する数を生成する数生成部と、前記数生成部が生成した数を、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式の係数に割り当てる割当部と、を備え、前記割当部は、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式の係数のうち、変数の組み合わせの種類が同じ項の係数をグループ化しておき、割り当て処理をグループ単位で実行する、情報処理装置が提供される。
【0014】
また、本技術の別の観点によれば、多次多変数多項式の組F=(f1,…,fm)を含む公開鍵を利用した公開鍵認証方式又は電子署名方式のアルゴリズムを実行するエンティティの間で共有されている情報から所定の関数を用いて、前記多次多変数多項式の組Fを構成する各項の係数に利用する数を生成する数生成部と、前記数生成部が生成した数を、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式の係数に割り当てる割当部と、を備え、前記割当部は、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式を2次形式で表現した場合の係数行列を行又は列毎にグループ化しておき、割り当て処理をグループ単位で実行する、情報処理装置が提供される。
【0015】
また、本技術の別の観点によれば、多次多変数多項式の組F=(f1,…,fm)を含む公開鍵を利用した公開鍵認証方式又は電子署名方式のアルゴリズムを実行するエンティティの間で共有されている情報から所定の関数を用いて前記多次多変数多項式の組Fを構成する各項の係数と同じ数だけ数を生成する数生成部と、前記証明者と前記認証者との間で予め決められた順序で前記数生成部が生成した数を、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式の係数に割り当てる割当部と、を備える、情報処理装置が提供される。
【0016】
また、本技術の別の観点によれば、多次多変数多項式の組F=(f1,…,fm)を含む公開鍵を利用した公開鍵認証方式又は電子署名方式のアルゴリズムを実行するエンティティの間で共有されている情報から所定の関数を用いて、前記多次多変数多項式の組Fを構成する各項の係数に利用する数を生成するステップと、生成した数を、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式の係数に割り当てるステップと、を含み、前記割り当てるステップでは、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式の係数のうち、変数の組み合わせの種類が同じ項の係数をグループ化しておき、割り当て処理をグループ単位で実行する、情報処理方法が提供される。
【0017】
また、本技術の別の観点によれば、多次多変数多項式の組F=(f1,…,fm)を含む公開鍵を利用した公開鍵認証方式又は電子署名方式のアルゴリズムを実行するエンティティの間で共有されている情報から所定の関数を用いて、前記多次多変数多項式の組Fを構成する各項の係数に利用する数を生成するステップと、生成した数を、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式の係数に割り当てるステップと、を含み、前記割り当てるステップでは、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式を2次形式で表現した場合の係数行列を行又は列毎にグループ化しておき、割り当て処理をグループ単位で実行する、情報処理方法が提供される。
【0018】
また、本技術の別の観点によれば、多次多変数多項式の組F=(f1,…,fm)を含む公開鍵を利用した公開鍵認証方式又は電子署名方式のアルゴリズムを実行するエンティティの間で共有されている情報から所定の関数を用いて前記多次多変数多項式の組Fを構成する各項の係数と同じ数だけ数を生成するステップと、前記証明者と前記認証者との間で予め決められた順序で前記数生成部が生成した数を、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式の係数に割り当てるステップと、を含む、情報処理方法が提供される。
【0019】
また、本技術の別の観点によれば、多次多変数多項式の組F=(f1,…,fm)を含む公開鍵を利用した公開鍵認証方式又は電子署名方式のアルゴリズムを実行するエンティティの間で共有されている情報から所定の関数を用いて、前記多次多変数多項式の組Fを構成する各項の係数に利用する数を生成する数生成機能と、前記数生成機能が生成した数を、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式の係数に割り当てる割当機能と、をコンピュータに実現させるためのプログラムであり、前記割当機能は、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式の係数のうち、変数の組み合わせの種類が同じ項の係数をグループ化しておき、割り当て処理をグループ単位で実行する、プログラムが提供される。
【0020】
また、本技術の別の観点によれば、多次多変数多項式の組F=(f1,…,fm)を含む公開鍵を利用した公開鍵認証方式又は電子署名方式のアルゴリズムを実行するエンティティの間で共有されている情報から所定の関数を用いて、前記多次多変数多項式の組Fを構成する各項の係数に利用する数を生成する数生成機能と、前記数生成機能が生成した数を、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式の係数に割り当てる割当機能と、をコンピュータに実現させるためのプログラムであり、前記割当機能は、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式を2次形式で表現した場合の係数行列を行又は列毎にグループ化しておき、割り当て処理をグループ単位で実行する、プログラムが提供される。
【0021】
また、本技術の別の観点によれば、多次多変数多項式の組F=(f1,…,fm)を含む公開鍵を利用した公開鍵認証方式又は電子署名方式のアルゴリズムを実行するエンティティの間で共有されている情報から所定の関数を用いて前記多次多変数多項式の組Fを構成する各項の係数と同じ数だけ数を生成する数生成機能と、前記証明者と前記認証者との間で予め決められた順序で前記数生成部が生成した数を、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式の係数に割り当てる割当機能と、をコンピュータに実現させるためのプログラムが提供される。
【0022】
また、本技術の別の観点によれば、上記のプログラムが記録された、コンピュータにより読み取り可能な記録媒体が提供される。
【発明の効果】
【0023】
以上説明したように本技術によれば、効率的に多変数多項式の係数を代入することが可能になる。
【図面の簡単な説明】
【0024】
【図1】公開鍵認証方式に係るアルゴリズムの構成について説明するための説明図である。
【図2】電子署名方式に係るアルゴリズムの構成について説明するための説明図である。
【図3】nパスの公開鍵認証方式に係るアルゴリズムの構成について説明するための説明図である。
【図4】3パスの公開鍵認証方式に係る効率的なアルゴリズムについて説明するための説明図である。
【図5】3パスの公開鍵認証方式に係る効率的なアルゴリズムの並列化について説明するための説明図である。
【図6】3パスの公開鍵認証方式に係る効率的なアルゴリズムについて説明するための説明図である。
【図7】5パスの公開鍵認証方式に係る効率的なアルゴリズムの構成例について説明するための説明図である。
【図8】5パスの公開鍵認証方式に係る効率的なアルゴリズムの並列化について説明するための説明図である。
【図9】5パスの公開鍵認証方式に係る効率的なアルゴリズムの並列化について説明するための説明図である。
【図10】3パスの公開鍵認証方式に係る効率的なアルゴリズムを電子署名方式のアルゴリズムに変形する方法について説明するための説明図である。
【図11】5パスの公開鍵認証方式に係る効率的なアルゴリズムを電子署名方式のアルゴリズムに変形する方法について説明するための説明図である。
【図12】ハッシュ関数の構造例について説明するための説明図である。
【図13】3パス方式に基づく電子署名方式に係る署名検証方法(通常の実装方法)について説明するための説明図である。
【図14】3パス方式に基づく電子署名方式に係る署名検証方法(メモリ削減方法)について説明するための説明図である。
【図15】5パス方式に基づく電子署名方式に係る署名検証方法(通常の実装方法)について説明するための説明図である。
【図16】5パス方式に基づく電子署名方式に係る署名検証方法(メモリ削減方法)について説明するための説明図である。
【図17】2進乱数から3進乱数を抽出する方法(抽出方法#1)について説明するための説明図である。
【図18】2進乱数から3進乱数を抽出する方法(抽出方法#2)について説明するための説明図である。
【図19】2進乱数から3進乱数を抽出する方法(抽出方法#3)について説明するための説明図である。
【図20】2進乱数から3進乱数を抽出する方法(抽出方法#3)について説明するための説明図である。
【図21】2進乱数から3進乱数を抽出する方法(抽出方法#3)について説明するための説明図である。
【図22】多変数多項式の係数を効率的に代入するためのデータ構造化手法(構造化手法#1)について説明するための説明図である。
【図23】多変数多項式の係数を効率的に代入するためのデータ構造化手法(構造化手法#1)について説明するための説明図である。
【図24】多変数多項式の係数を効率的に代入するためのデータ構造化手法(構造化手法#1)について説明するための説明図である。
【図25】多変数多項式の係数を効率的に代入するためのデータ構造化手法(構造化手法#1)について説明するための説明図である。
【図26】多変数多項式の係数を効率的に代入するためのデータ構造化手法(構造化手法#1)について説明するための説明図である。
【図27】多変数多項式の係数を効率的に代入するためのデータ構造化手法(構造化手法#2)について説明するための説明図である。
【図28】本技術の各実施形態に係るアルゴリズムを実行することが可能な情報処理装置のハードウェア構成例について説明するための説明図である。
【発明を実施するための形態】
【0025】
以下に添付図面を参照しながら、本技術の好適な実施の形態について詳細に説明する。なお、本明細書及び図面において、実質的に同一の機能構成を有する構成要素については、同一の符号を付することにより重複説明を省略する。
【0026】
[説明の流れについて]
ここで、以下に記載する本技術の実施形態に関する説明の流れについて簡単に述べる。まず、図1を参照しながら、公開鍵認証方式のアルゴリズム構成について説明する。次いで、図2を参照しながら、電子署名方式のアルゴリズム構成について説明する。次いで、図3を参照しながら、nパスの公開鍵認証方式について説明する。
【0027】
次いで、図4〜図6を参照しながら、3パスの公開鍵認証方式に係るアルゴリズムの構成例について説明する。次いで、図7〜図9を参照しながら、5パスの公開鍵認証方式に係るアルゴリズムの構成例について説明する。次いで、図10及び図11を参照しながら、3パス及び5パスの公開鍵認証方式に係る効率的なアルゴリズムを電子署名方式のアルゴリズムに変形する方法について説明する。
【0028】
次いで、図12〜図16を参照しながら、本実施形態に係る電子署名方式のアルゴリズムを実行する際に署名検証に要するメモリ量を削減する方法について説明する。次いで、図17〜図21を参照しながら、2進乱数から3進乱数を効率的に抽出する方法について説明する。次いで、図22〜図27を参照しながら、多変数多項式の係数を効率的に代入する方法について説明する。次いで、図28を参照しながら、本技術の実施形態に係る各アルゴリズムを実現することが可能な情報処理装置のハードウェア構成例について説明する。最後に、本実施形態の技術的思想について纏め、当該技術的思想から得られる作用効果について簡単に説明する。
【0029】
(説明項目)
1:はじめに
1−1:公開鍵認証方式のアルゴリズム
1−2:電子署名方式のアルゴリズム
1−3:nパスの公開鍵認証方式
2:3パスの公開鍵認証方式に係るアルゴリズムの構成
2−1:具体的なアルゴリズムの構成例
2−2:並列化アルゴリズムの構成例
2−3:3次多変数多項式に基づくアルゴリズムの構成例
3:5パスの公開鍵認証方式に係るアルゴリズムの構成
3−1:具体的なアルゴリズムの構成例
3−2:並列化アルゴリズムの構成例
3−3:3次多変数多項式に基づくアルゴリズムの構成例
4:電子署名方式への変形
4−1:3パスの公開鍵認証方式から電子署名方式への変形
4−2:5パスの公開鍵認証方式から電子署名方式への変形
5:署名検証に要するメモリ量の削減方法について
5−1:ハッシュ関数の構造について
5−2:3パス方式に基づく電子署名方式への適用例
5−3:5パス方式に基づく電子署名方式への適用例
6:2進数の乱数列から3進数の乱数列を抽出する方法について
6−1:抽出方法#1(2ビット区切り)
6−2:抽出方法#2(区切りなし)
6−3:抽出方法#3(kビット区切り)
6−3−1:基本構成
6−3−2:追加抽出方法
7:多変数多項式の係数を効率的に代入する方法について
7−1:基本的な取り決め
7−2:データの構造化
7−2−1:構造化手法#1
7−2−2:構造化手法#2
7−2−3:構造化手法#3
8:ハードウェア構成例
9:まとめ
【0030】
<1:はじめに>
本実施形態は、多次多変数連立方程式に対する求解問題の困難性に安全性の根拠をおく公開鍵認証方式及び電子署名方式に関する。但し、本実施形態は、HFE電子署名方式などの従来手法とは異なり、効率的に解く手段(トラップドア)を持たない多次多変数連立方程式を利用する公開鍵認証方式及び電子署名方式に関する。まず、公開鍵認証方式のアルゴリズム、電子署名方式のアルゴリズム、及びnパスの公開鍵認証方式について、その概要を簡単に説明する。
【0031】
[1−1:公開鍵認証方式のアルゴリズム]
まず、図1を参照しながら、公開鍵認証方式のアルゴリズムについて概要を説明する。図1は、公開鍵認証方式のアルゴリズムについて概要を説明するための説明図である。
【0032】
公開鍵認証は、ある人(証明者)が、公開鍵pk及び秘密鍵skを利用して、他の人(検証者)に本人であることを納得させるために利用される。例えば、証明者Aの公開鍵pkAは、検証者Bに公開される。一方、証明者Aの秘密鍵skAは、証明者Aにより秘密に管理される。公開鍵認証の仕組みにおいては、公開鍵pkAに対応する秘密鍵skAを知る者が証明者A本人であるとみなされる。
【0033】
公開鍵認証の仕組みを利用して証明者Aが証明者A本人であることを検証者Bに証明するには、対話プロトコルを介して、証明者Aが公開鍵pkAに対応する秘密鍵skAを知っているという証拠を検証者Bに提示すればよい。そして、証明者Aが秘密鍵skAを知っているという証拠が検証者Bに提示され、その証拠を検証者Bが確認し終えた場合、証明者Aの正当性(本人であること)が証明されたことになる。
【0034】
但し、公開鍵認証の仕組みには、安全性を担保するために以下の条件が求められる。
【0035】
1つ目の条件は、「対話プロトコルを実行した際に秘密鍵skを持たない偽証者により偽証が成立してしまう確率を限りなく小さくする」ことである。この1つ目の条件が成り立つことを「健全性」と呼ぶ。つまり、健全性とは、「秘密鍵skを持たない偽証者により、対話プロトコルの実行中に無視できない確率で偽証が成立することはないこと」と言い換えられる。2つ目の条件は、「対話プロトコルを実行したとしても、証明者Aが有する秘密鍵skAの情報が検証者Bに一切漏れることがない」ことである。この2つ目の条件が成り立つことを「零知識性」と呼ぶ。
【0036】
安全に公開鍵認証を行うには、健全性及び零知識性を有する対話プロトコルを利用する必要がある。仮に、健全性及び零知識性を有しない対話プロトコルを用いて認証処理を行った場合には、偽証された可能性及び秘密鍵の情報が漏れてしまった可能性が否定できないため、処理自体が成功裡に完了しても証明者の正当性を証明したことにはならない。従って、対話プロトコルの健全性及び零知識性を如何に保証するかが重要になる。
【0037】
(モデル)
公開鍵認証方式のモデルには、図1に示すように、証明者と検証者という2つのエンティティが存在する。証明者は、鍵生成アルゴリズムGenを用いて、証明者固有の秘密鍵skと公開鍵pkの組を生成する。次いで、証明者は、鍵生成アルゴリズムGenを用いて生成した秘密鍵skと公開鍵pkの組を利用して検証者と対話プロトコルを実行する。このとき、証明者は、証明者アルゴリズムPを利用して対話プロトコルを実行する。上記の通り、証明者は、証明者アルゴリズムPを利用し、対話プロトコルの中で秘密鍵skを保有している証拠を検証者に提示する。
【0038】
一方、検証者は、検証者アルゴリズムVを利用して対話プロトコルを実行し、証明者が公開している公開鍵に対応する秘密鍵を、その証明者が保有しているか否かを検証する。つまり、検証者は、証明者が公開鍵に対応する秘密鍵を保有しているか否かを検証するエンティティである。このように、公開鍵認証方式のモデルは、証明者と検証者という2つのエンティティ、及び、鍵生成アルゴリズムGen、証明者アルゴリズムP、検証者アルゴリズムVという3つのアルゴリズムにより構成される。
【0039】
なお、以下の説明において、「証明者」「検証者」という表現を用いるが、これらの表現はあくまでもエンティティを意味するものである。従って、鍵生成アルゴリズムGen、証明者アルゴリズムPを実行する主体は、「証明者」のエンティティに対応する情報処理装置である。同様に、検証者アルゴリズムVを実行する主体は、情報処理装置である。これら情報処理装置のハードウェア構成は、例えば、図28に示した通りである。つまり、鍵生成アルゴリズムGen、証明者アルゴリズムP、検証者アルゴリズムVは、ROM904、RAM906、記憶部920、リムーバブル記録媒体928などに記録されたプログラムに基づいてCPU902などにより実行される。
【0040】
(鍵生成アルゴリズムGen)
鍵生成アルゴリズムGenは、証明者により利用される。鍵生成アルゴリズムGenは、証明者に固有の秘密鍵skと公開鍵pkとの組を生成するアルゴリズムである。鍵生成アルゴリズムGenにより生成された公開鍵pkは公開される。そして、公開された公開鍵pkは、検証者により利用される。一方、鍵生成アルゴリズムGenにより生成された秘密鍵skは、証明者が秘密に管理する。そして、証明者により秘密に管理される秘密鍵skは、公開鍵pkに対応する秘密鍵skを証明者が保有していることを検証者に対して証明するために利用される。形式的に、鍵生成アルゴリズムGenは、セキュリティパラメータ1λ(λは0以上の整数)を入力とし、秘密鍵skと公開鍵pkを出力するアルゴリズムとして、下記の式(1)のように表現される。
【0041】
【数1】

【0042】
(証明者アルゴリズムP)
証明者アルゴリズムPは、証明者により利用される。証明者アルゴリズムPは、公開鍵pkに対応する秘密鍵skを証明者が保有していることを検証者に対して証明するためのアルゴリズムである。つまり、証明者アルゴリズムPは、秘密鍵skと公開鍵pkとを入力とし、対話プロトコルを実行するアルゴリズムである。
【0043】
(検証者アルゴリズムV)
検証者アルゴリズムVは、検証者により利用される。検証者アルゴリズムVは、対話プロトコルの中で、公開鍵pkに対応する秘密鍵skを証明者が保有しているか否かを検証するアルゴリズムである。検証者アルゴリズムVは、公開鍵pkを入力とし、対話プロトコルの実行結果に応じて0又は1(1bit)を出力するアルゴリズムである。なお、検証者は、検証者アルゴリズムVが0を出力した場合には証明者が不正なものであると判断し、1を出力した場合には証明者が正当なものであると判断する。形式的に、検証者アルゴリズムVは、下記の式(2)のように表現される。
【0044】
【数2】

【0045】
上記の通り、意味のある公開鍵認証を実現するには、対話プロトコルが健全性及び零知識性という2つの条件を満たしている必要がある。しかし、証明者が秘密鍵skを保有していることを証明するためには、証明者が秘密鍵skに依存した手続きを実行し、その結果を検証者に通知した上で、その通知内容に基づく検証を検証者に実行させる必要がある。秘密鍵skに依存した手続きを実行するのは、健全性を担保するために必要である。一方で、秘密鍵skの情報が一切検証者に漏れないようにする必要がある。そのため、これらの要件を満たすように、上記の鍵生成アルゴリズムGen、証明者アルゴリズムP、検証者アルゴリズムVを巧妙に設計する必要がある。
【0046】
以上、公開鍵認証方式のアルゴリズムについて、その概要を説明した。
【0047】
[1−2:電子署名方式のアルゴリズム]
次に、図2を参照しながら、電子署名方式のアルゴリズムについて概要を説明する。図2は、電子署名方式のアルゴリズムについて概要を説明するための説明図である。
【0048】
紙文書とは異なり、ある電子化されたデータに対して押印したり署名を記載したりすることはできない。そのため、電子化されたデータの作成者を証明するためには、紙文書に押印したり署名を記載したりするのと同等の効果が得られる電子的な仕組みを必要とする。この仕組みが電子署名である。電子署名とは、データの作成者しか知らない署名データをデータに関連付けて受領者に提供し、その署名データを受領者側で検証する仕組みのことを言う。
【0049】
(モデル)
電子署名方式のモデルには、図2に示すように、署名者及び検証者という2つのエンティティが存在する。そして、電子署名方式のモデルは、鍵生成アルゴリズムGen、署名生成アルゴリズムSig、署名検証アルゴリズムVerという3つのアルゴリズムにより構成される。
【0050】
署名者は、鍵生成アルゴリズムGenを利用して署名者固有の署名鍵skと検証鍵pkとの組を生成する。また、署名者は、署名生成アルゴリズムSigを利用して文書Mに付与する電子署名σを生成する。つまり、署名者は、文書Mに電子署名を付与するエンティティである。一方、検証者は、署名検証アルゴリズムVerを利用して文書Mに付与された電子署名σを検証する。つまり、検証者は、文書Mの作成者が署名者であるか否かを確認するために、電子署名σを検証するエンティティである。
【0051】
なお、以下の説明において、「署名者」「検証者」という表現を用いるが、これらの表現はあくまでもエンティティを意味するものである。従って、鍵生成アルゴリズムGen、署名生成アルゴリズムSigを実行する主体は、「署名者」のエンティティに対応する情報処理装置である。同様に、署名検証アルゴリズムVerを実行する主体は、情報処理装置である。これら情報処理装置のハードウェア構成は、例えば、図28に示した通りである。つまり、鍵生成アルゴリズムGen、署名生成アルゴリズムSig、署名検証アルゴリズムVerは、ROM904、RAM906、記憶部920、リムーバブル記録媒体928などに記録されたプログラムに基づいてCPU902などにより実行される。
【0052】
(鍵生成アルゴリズムGen)
鍵生成アルゴリズムGenは、署名者により利用される。鍵生成アルゴリズムGenは、署名者固有の署名鍵skと検証鍵pkとの組を生成するアルゴリズムである。鍵生成アルゴリズムGenにより生成された検証鍵pkは公開される。一方、鍵生成アルゴリズムGenにより生成された署名鍵skは、署名者により秘密に管理される。そして、署名鍵skは、文書Mに付与される電子署名σの生成に利用される。例えば、鍵生成アルゴリズムGenは、セキュリティパラメータ1λ(λは0以上の整数)を入力とし、署名鍵sk及び公開鍵pkを出力する。この場合、鍵生成アルゴリズムGenは、形式的に、下記の式(3)のように表現することができる。
【0053】
【数3】

【0054】
(署名生成アルゴリズムSig)
署名生成アルゴリズムSigは、署名者により利用される。署名生成アルゴリズムSigは、文書Mに付与される電子署名σを生成するアルゴリズムである。署名生成アルゴリズムSigは、署名鍵skと文書Mとを入力とし、電子署名σを出力するアルゴリズムである。この署名生成アルゴリズムSigは、形式的に、下記の式(4)のように表現することができる。
【0055】
【数4】

【0056】
(署名検証アルゴリズムVer)
署名検証アルゴリズムVerは、検証者により利用される。署名検証アルゴリズムVerは、電子署名σが文書Mに対する正当な電子署名であるか否かを検証するアルゴリズムである。署名検証アルゴリズムVerは、署名者の検証鍵pk、文書M、電子署名σを入力とし、0又は1(1bit)を出力するアルゴリズムである。この署名検証アルゴリズムVerは、形式的に、下記の式(5)のように表現することができる。なお、検証者は、署名検証アルゴリズムVerが0を出力した場合(公開鍵pkが文書Mと電子署名σを拒否する場合)に電子署名σが不当であると判断し、1を出力した場合(公開鍵pkが文書Mと電子署名σを受理する場合)に電子署名σが正当であると判断する。
【0057】
【数5】

【0058】
以上、電子署名方式のアルゴリズムについて、その概要を説明した。
【0059】
[1−3:nパスの公開鍵認証方式]
次に、図3を参照しながら、nパスの公開鍵認証方式について説明する。図3は、nパスの公開鍵認証方式について説明するための説明図である。
【0060】
上記の通り、公開鍵認証方式は、対話プロトコルの中で、証明者が公開鍵pkに対応する秘密鍵skを保有していることを検証者に証明する認証方式である。また、対話プロトコルは、健全性及び零知識性という2つの条件を満たす必要がある。そのため、対話プロトコルの中では、図3に示すように、証明者及び検証者の双方がそれぞれ処理を実行しながらn回の情報交換を行う。
【0061】
nパスの公開鍵認証方式の場合、証明者アルゴリズムPを用いて証明者により処理(工程#1)が実行され、情報T1が検証者に送信される。次いで、検証者アルゴリズムVを用いて検証者により処理(工程#2)が実行され、情報T2が証明者に送信される。さらに、k=3〜nについて処理の実行及び情報Tkの送信が順次行われ、最後に処理(工程#n+1)が実行される。このように、情報がn回送受信される方式のことを「nパス」の公開鍵認証方式と呼ぶ。
【0062】
以上、nパスの公開鍵認証方式について説明した。
【0063】
<2:3パスの公開鍵認証方式に係るアルゴリズムの構成>
以下、3パスの公開鍵認証方式に係るアルゴリズムについて説明する。なお、以下の説明において、3パスの公開鍵認証方式のことを「3パス方式」と呼ぶ場合がある。
【0064】
[2−1:具体的なアルゴリズムの構成例(図4)]
まず、図4を参照しながら、3パス方式に係る具体的なアルゴリズムの構成例について紹介する。図4は、3パス方式に係る具体的なアルゴリズムの構成について説明するための説明図である。ここでは、公開鍵pkの一部として2次多項式の組(f1(x),…,fm(x))を利用する場合について考える。但し、2次多項式fi(x)は、下記の式(6)のように表現されるものとする。また、ベクトル(x1,…,xn)をxと表記し、2次多項式の組(f1(x),…,fm(x))を多変数多項式F(x)と表記することにする。
【0065】
【数6】

【0066】
また、2次多項式の組(f1(x),…,fm(x))は、下記の式(7)のように表現することができる。また、A1,…,Amは、n×n行列である。さらに、b1,…,bmはそれぞれn×1ベクトルである。
【0067】
【数7】

【0068】
この表現を用いると、多変数多項式Fは、下記の式(8)及び式(9)のように表現することができる。この表現が成り立つことは、下記の式(10)から容易に確認することができる。
【0069】
【数8】

【0070】
このようにF(x+y)をxに依存する第1の部分と、yに依存する第2の部分と、x及びyの両方に依存する第3の部分とに分けたとき、第3の部分に対応する項G(x,y)は、x及びyについて双線形になる。以下、項G(x,y)を双線形項と呼ぶ場合がある。この性質を利用すると、効率的なアルゴリズムを構築することが可能になる。
【0071】
例えば、ベクトルt0∈Kn、e0∈Kmを用いて、多変数多項式F(x+r)のマスクに利用する多変数多項式F1(x)をF1(x)=G(x,t0)+e0と表現する。この場合、多変数多項式F(x+r0)とG(x)との和は、下記の式(11)のように表現される。ここで、t1=r0+t0、e1=F(r0)+e0とおけば、多変数多項式F2(x)=F(x+r0)+F1(x)は、ベクトルt1∈Kn、e1∈Kmにより表現することができる。そのため、F1(x)=G(x,t0)+e0に設定すれば、Kn上のベクトル及びKm上のベクトルを用いてF1及びF2を表現できるようになり、通信に必要なデータサイズの少ない効率的なアルゴリズムを実現することが可能になる。
【0072】
【数9】

【0073】
なお、F2(或いはF1)からr0に関する情報が一切漏れることはない。例えば、e1及びt1(或いはe0及びt0)を与えられても、e0及びt0(或いはe1及びt1)を知らない限り、r0の情報を一切知ることはできない。従って、零知識性が担保される。以下、上記の論理に基づいて構築された3パス方式のアルゴリズムについて説明する。ここで説明する3パス方式のアルゴリズムは、以下のような鍵生成アルゴリズムGen、証明者アルゴリズムP、検証者アルゴリズムVにより構成される。
【0074】
(鍵生成アルゴリズムGen)
鍵生成アルゴリズムGenは、環K上で定義されるm本の多変数多項式f1(x1,…,xn),…,fm(x1,…,xn)、及びベクトルs=(s1,…,sn)∈Knを生成する。次に、鍵生成アルゴリズムGenは、y=(y1,…,ym)←(f1(s),…,fm(s))を計算する。そして、鍵生成アルゴリズムGenは、(f1(x1,…,xn),…,fm(x1,…,xn),y)を公開鍵pkに設定し、sを秘密鍵に設定する。
【0075】
(証明者アルゴリズムP、検証者アルゴリズムV)
以下、図4を参照しながら、対話プロトコルの中で証明者アルゴリズムPが実行する処理及び検証者アルゴリズムVが実行する処理について説明する。この対話プロトコルの中で、証明者は、秘密鍵sの情報を検証者に一切漏らさずに、「自身がy=F(s)を満たすsを知っていること」を検証者に示す。一方、検証者は、証明者がy=F(s)を満たすsを知っているか否かを検証する。なお、公開鍵pkは、検証者に公開されているものとする。また、秘密鍵sは、証明者により秘密に管理されているものとする。以下、図4に示したフローチャートに沿って説明を進める。
【0076】
工程#1:
図4に示すように、まず、証明者アルゴリズムPは、ランダムにベクトルr0,t0∈Kn及びe0∈Kmを生成する。次いで、証明者アルゴリズムPは、r1←s−r0を計算する。この計算は、秘密鍵sをベクトルr0によりマスクする操作に相当する。さらに、証明者アルゴリズムPは、t1←r0−t0を計算する。次いで、証明者アルゴリズムPは、e1←F(r0)−e0を計算する。
【0077】
工程#1(続き):
次いで、証明者アルゴリズムPは、c0←H(r1,G(t0,r1)+e0)を計算する。次いで、証明者アルゴリズムPは、c1←H(t0,e0)を計算する。次いで、証明者アルゴリズムPは、c2←H(t1,e1)を計算する。工程#1で生成されたメッセージ(c0,c1,c2)は、検証者アルゴリズムVに送られる。
【0078】
工程#2:
メッセージ(c0,c1,c2)を受け取った検証者アルゴリズムVは、3つの検証パターンのうち、どの検証パターンを利用するかを選択する。例えば、検証者アルゴリズムVは、検証パターンの種類を表す3つの数値{0,1,2}の中から1つの数値を選択し、選択した数値を要求Chに設定する。この要求Chは証明者アルゴリズムPに送られる。
【0079】
工程#3:
要求Chを受け取った証明者アルゴリズムPは、受け取った要求Chに応じて検証者アルゴリズムVに送る返答Rspを生成する。Ch=0の場合、証明者アルゴリズムPは、返答Rsp=(r0,t1,e1)を生成する。Ch=1の場合、証明者アルゴリズムPは、返答Rsp=(r1,t0,e0)を生成する。Ch=2の場合、証明者アルゴリズムPは、返答Rsp=(r1,t1,e1)を生成する。工程#3で生成された返答Rspは、検証者アルゴリズムVに送られる。
【0080】
工程#4:
返答Rspを受け取った検証者アルゴリズムVは、受け取った返答Rspを利用して以下の検証処理を実行する。
【0081】
Ch=0の場合、検証者アルゴリズムVは、c1=H(r0−t1,F(r0)−e1)の等号が成り立つか否かを検証する。さらに、検証者アルゴリズムVは、c2=H(t1,e1)の等号が成り立つか否かを検証する。検証者アルゴリズムVは、これらの検証が全て成功した場合に認証成功を示す値1を出力し、検証に失敗があった場合に認証失敗を示す値0を出力する。
【0082】
Ch=1の場合、検証者アルゴリズムVは、c0=H(r1,G(t0,r1)+e0)の等号が成り立つか否かを検証する。さらに、検証者アルゴリズムVは、c1=H(t0,e0)の等号が成り立つか否かを検証する。検証者アルゴリズムVは、これらの検証が全て成功した場合に認証成功を示す値1を出力し、検証に失敗があった場合に認証失敗を示す値0を出力する。
【0083】
Ch=2の場合、検証者アルゴリズムVは、c0=H(r1,y−F(r1)−G(t1,r1)−e1)の等号が成り立つか否かを検証する。さらに、検証者アルゴリズムVは、c2=H(t1,e1)の等号が成り立つか否かを検証する。検証者アルゴリズムVは、これらの検証が全て成功した場合に認証成功を示す値1を出力し、検証に失敗があった場合に認証失敗を示す値0を出力する。
【0084】
以上、3パス方式に係る効率的なアルゴリズムの構成例について説明した。
【0085】
[2−2:並列化アルゴリズムの構成例(図5)]
次に、図5を参照しながら、図4に示した3パス方式のアルゴリズムを並列化する方法について説明する。なお、鍵生成アルゴリズムGenの構成については説明を省略する。
【0086】
さて、上記の対話プロトコルを適用すれば、偽証が成功する確率を2/3以下に抑制することができる。従って、この対話プロトコルを2回実行すれば、偽証が成功する確率を(2/3)2以下に抑制することができる。さらに、この対話プロトコルをN回実行すると、偽証が成功する確率は(2/3)Nとなり、Nを十分に大きい数(例えば、N=140)にすれば、偽証が成功する確率は無視できる程度に小さくなる。
【0087】
対話プロトコルを複数回実行する方法としては、例えば、メッセージ、要求、返答のやり取りを逐次的に複数回繰り返す直列的な方法と、1回分のやり取りで複数回分のメッセージ、要求、返答のやり取りを行う並列的な方法とが考えられる。さらに、直列的な方法と並列的な方法とを組み合わせたハイブリッド型の方法も考えられる。ここでは、図5を参照しながら、3パス方式に係る上記の対話プロトコルを並列的に実行するアルゴリズム(以下、並列化アルゴリズム)について説明する。
【0088】
工程#1:
図5に示すように、まず、証明者アルゴリズムPは、i=1〜Nについて以下の処理(1)〜処理(6)を実行する。
処理(1):証明者アルゴリズムPは、ランダムにベクトルr0i,t0i∈Kn及びe0i∈Kmを生成する。
処理(2):証明者アルゴリズムPは、r1i←s−r0iを計算する。この計算は、秘密鍵sをベクトルr0iによりマスクする操作に相当する。さらに、証明者アルゴリズムPは、t1i←r0i+t0iを計算する。
処理(3):証明者アルゴリズムPは、e1i←F(r0i)−e0iを計算する。
処理(4):証明者アルゴリズムPは、c0i←H(r1i,G(r1i,t0i)+e0i)を計算する。
処理(5):証明者アルゴリズムPは、c1i←H(t0i,e0i)を計算する。
処理(6):証明者アルゴリズムPは、c2i←H(t1i,e1i)を計算する。
【0089】
工程#1(続き)
i=1〜Nについて上記の処理(1)〜処理(6)を実行した後、証明者アルゴリズムPは、Cmt←H(c01,c11,c21,…,c0N,c1N,c2N)を計算する。工程#1で生成されたハッシュ値Cmtは、検証者アルゴリズムVに送られる。このように、メッセージ(c01,c11,c21,…,c0N,c1N,c2N)をハッシュ値に変換してから検証者アルゴリズムVに送ることで、通信量を削減することが可能になる。
【0090】
工程#2:
ハッシュ値Cmtを受け取った検証者アルゴリズムVは、i=1〜Nのそれぞれについて、3つの検証パターンのうち、どの検証パターンを利用するかを選択する。例えば、検証者アルゴリズムVは、i=1〜Nのそれぞれについて、検証パターンの種類を表す3つの数値{0,1,2}の中から1つの数値を選択し、選択した数値を要求Chiに設定する。要求Ch1,…,ChNは、証明者アルゴリズムPに送られる。
【0091】
工程#3:
要求Ch1,…,ChNを受け取った証明者アルゴリズムPは、受け取った要求Ch1,…,ChNのそれぞれ応じて検証者アルゴリズムVに送る返答Rsp1,…,RspNを生成する。Chi=0の場合、証明者アルゴリズムPは、Rspi=(r0i,t1i,e1i,c0i)を生成する。Chi=1の場合、証明者アルゴリズムPは、Rspi=(r1i,t0i,e0i,c2i)を生成する。Chi=2の場合、証明者アルゴリズムPは、Rspi=(r1i,t1i,e1i,c1i)を生成する。
【0092】
工程#3で生成された返答Rsp1,…,RspNは、検証者アルゴリズムVに送られる。
【0093】
工程#4:
返答Rsp1,…,RspNを受け取った検証者アルゴリズムVは、受け取った返答Rsp1,…,RspNを利用して以下の処理(1)〜処理(3)をi=1〜Nについて実行する。但し、検証者アルゴリズムVは、Chi=0の場合に処理(1)を実行し、Chi=1の場合に処理(2)を実行し、Chi=2の場合に処理(3)を実行する。
【0094】
処理(1):Chi=0の場合、検証者アルゴリズムVは、Rspiから(r0i,t1i,e1i,c0i)を取り出す。次いで、検証者アルゴリズムVは、c1i=H(r0i−t1i,F(r0i)−e1i)を計算する。さらに、検証者アルゴリズムVは、c2i=H(t1i,e1i)を計算する。そして、検証者アルゴリズムVは、(c0i,c1i,c2i)を保持する。
【0095】
処理(2):Chi=1の場合、検証者アルゴリズムVは、Rspiから(r1i,t0i,e0i,c2i)を取り出す。次いで、検証者アルゴリズムVは、c0i=H(r1i,G(t0i,r1i)+e0i)を計算する。さらに、検証者アルゴリズムVは、c1i=H(t0i,e0i)を計算する。そして、検証者アルゴリズムVは、(c0i,c1i,c2i)を保持する。
【0096】
処理(3):Chi=2の場合、検証者アルゴリズムVは、Rspiから(r1i,t1i,e1i,c1i)を取り出す。次いで、検証者アルゴリズムVは、c0i=H(r1i,y−F(r1i)−G(t1i,r1i)−e1i)を計算する。さらに、検証者アルゴリズムVは、c2i=H(t1i,e1i)を計算する。そして、検証者アルゴリズムVは、(c0i,c1i,c2i)を保持する。
【0097】
処理(1)〜処理(3)をi=1〜Nについて実行した後、検証者アルゴリズムVは、Cmt=H(c01,c11,c21,…,c0N,c1N,c2N)の等号が成り立つか否かを検証する。検証者アルゴリズムVは、この検証が成功した場合に認証成功を示す値1を出力し、検証に失敗した場合に認証失敗を示す値0を出力する。
【0098】
以上、3パス方式に係る効率的な並列化アルゴリズムの構成例について説明した。
【0099】
[2−3:3次多変数多項式に基づくアルゴリズムの構成例]
次に、下記の式(12)で表現される環R上の3次多項式flを利用した効率的なアルゴリズムの構築方法について検討してみたい。3次多項式flの組で表現される多変数多項式F=(f1,…,fm)は、下記の式(13)の関係を満たす。但し、Gx(x,y)は、xに関して1次となる項を表す。また、Gy(x,y)は、yに関して1次となる項を表す。Gx=(gx1,…,gxm)、Gy=(gy1,…,gym)と表現すると、gxl及びgylは、それぞれ下記の式(14)及び式(15)のように展開することができる。但し、gxlの右辺第2項は、x及びyのいずれに関しても1次であるため、gylに含めてもよい。
【0100】
【数10】

【0101】
上記の式(14)及び式(15)から分かるように、Gx(x,y)及びGy(x,y)は、x及びyについて加法準同型になっている。そこで、これらの性質を利用し、2次多項式fiを利用した効率的なアルゴリズムの構築方法と同様に、新たな変数r0,r1,t0,u0,e0を導入して公開鍵F(s)を分割する。
【0102】
多項式Gx,Gyが加法準同型であるから、変数r0,r1,t0,u0,e0を用いて、下記の式(16)〜式(19)の関係が成り立つ。下記の式(16)〜式(19)は、(r0,t0,u0,e0)で再現可能な第1の部分と、(r0,u1,e1)で再現可能な第2の部分と、(r1,t0,e0)で再現可能な第3の部分と、(r1,t1,u1,e1)で再現可能な第4の部分と、に分けることができる。
【0103】
例えば、下記の式(17)に含まれる「r0,t0」、下記の式(18)に含まれる「u0」、下記の式(19)に含まれる「F(r0),Gy(r0,u0),e0」、は、第1の部分である。また、下記の式(19)に含まれる「Gy(r0,u1),e1」は、第2の部分である。さらに、下記の式(16)に含まれる「e0,Gx(r0,r1)」は、第3の部分である。そして、下記の式(16)に含まれる「e1,F(r1),Gx(t1,r1)」、下記の式(17)に含まれる「t1」、下記の式(18)に含まれる「u1」は、第4の部分である。
【0104】
言い換えると、下記の式(16)は第3及び第4の部分で構成され、下記の式(17)及び下記の式(18)は第1及び第4の部分で構成され、下記の式(19)は第1及び第2の部分で構成されている。このように、下記の式(16)〜式(19)は、それぞれ2種類の部分で構成されている。
【0105】
また、秘密鍵sの定義及び下記の式(16)〜式(19)の関係から、(r0,t0,u0,e0)、(r0,u1,e1)、(r1,t0,e0)、(r1,t1,u1,e1)のいずれか1つを用いても秘密鍵sは得られないことが保証される。これらの性質を利用すると、例えば、環R上の3次多項式flを利用した効率的なアルゴリズム(以下、拡張アルゴリズム)を構築することができる。
【0106】
【数11】

【0107】
以下、具体的な拡張アルゴリズムの構成例について説明する。拡張アルゴリズムの設計に関する基本的なポイントは、下記の式(20)〜式(22)で表現されるメッセージを検証者に送ること、及び第1〜第4の部分のいずれかに関する検証を行うことの2点である。但し、この検証だけでは、第3の部分に含まれる「r1」と第4の部分に含まれる「r1」とが等しいかを検証することができない。同様に、第1の部分に含まれる「r0」と第2の部分に含まれる「r0」とが等しいか、第1の部分に含まれる「t0,e0」と第3の部分に含まれる「t0,e0」とが等しいかも検証することができない。さらに、第2の部分に含まれる「u1,e1」と第4の部分に含まれる「u1,e1」とが等しいかも検証することができない。そこで、以下では、これらの検証も可能にした構成例を紹介する。
【0108】
【数12】

【0109】
以下、図6を参照しながら、3パス方式に係る拡張アルゴリズムの構成例について説明する。なお、鍵生成アルゴリズムGenの構成については説明を省略する。
【0110】
工程#1:
図6に示すように、証明者アルゴリズムPは、ランダムにベクトルr0,t0,u0∈Kn及びe0∈Kmを生成する。次いで、証明者アルゴリズムPは、r1←s−r0を計算する。この計算は、秘密鍵sをベクトルr0によりマスクする操作に相当する。次いで、証明者アルゴリズムPは、t1←r0−t0を計算する。次いで、証明者アルゴリズムPは、u1←r1−u0を計算する。次いで、証明者アルゴリズムPは、e1←F(r0)−e0を計算する。
【0111】
工程#1(続き):
次いで、証明者アルゴリズムPは、c0←H(r1,Gx(t0,r1)+e0)を計算する。次いで、証明者アルゴリズムPは、c1←H(r0−t0,u0)を計算する。次いで、証明者アルゴリズムPは、c2←H(r0,e1−Gy(r0,u1))を計算する。次いで、証明者アルゴリズムPは、c3←H(t0,e0)を計算する。次いで、証明者アルゴリズムPは、c4←H(u1,e1)を計算する。工程#1で生成されたメッセージ(c0,c1,c2,c3,c4)は、検証者アルゴリズムVに送られる。
【0112】
工程#2:
メッセージ(c0,c1,c2,c3,c4)を受け取った検証者アルゴリズムVは、4つの検証パターンのうち、どの検証パターンを利用するかを選択する。例えば、検証者アルゴリズムVは、検証パターンの種類を表す4つの数値{0,1,2,3}の中から1つの数値を選択し、選択した数値を要求Chに設定する。この要求Chは証明者アルゴリズムPに送られる。
【0113】
工程#3:
要求Chを受け取った証明者アルゴリズムPは、受け取った要求Chに応じて検証者アルゴリズムVに送る返答Rspを生成する。Ch=0の場合、証明者アルゴリズムPは、返答Rsp=(r0,t0,u0,e0)を生成する。Ch=1の場合、証明者アルゴリズムPは、返答Rsp=(r0,u1,e1)を生成する。Ch=2の場合、証明者アルゴリズムPは、返答Rsp=(r1,t0,e0)を生成する。Ch=3の場合、証明者アルゴリズムPは、返答Rsp=(r1,t1,u1,e1)を生成する。工程#3で生成された返答Rspは、検証者アルゴリズムVに送られる。
【0114】
工程#4:
返答Rspを受け取った検証者アルゴリズムVは、受け取った返答Rspを利用して以下の検証処理を実行する。
【0115】
Ch=0の場合、検証者アルゴリズムVは、c1=H(r0−t0,u0)の等号が成り立つか否かを検証する。次いで、検証者アルゴリズムVは、c2=H(r0,F(r0)+Gy(r0,u0)−e0)の等号が成り立つか否かを検証する。次いで、検証者アルゴリズムVは、c3=H(t0,e0)の等号が成り立つか否かを検証する。検証者アルゴリズムVは、これらの検証が全て成功した場合に認証成功を示す値1を出力し、検証に失敗があった場合に認証失敗を示す値0を出力する。
【0116】
Ch=1の場合、検証者アルゴリズムVは、c2=H(r0,e1−Gy(r0,u1))の等号が成り立つか否かを検証する。次いで、検証者アルゴリズムVは、c4=H(u1,e1)の等号が成り立つか否かを検証する。検証者アルゴリズムVは、これらの検証が全て成功した場合に認証成功を示す値1を出力し、検証に失敗があった場合に認証失敗を示す値0を出力する。
【0117】
Ch=2の場合、検証者アルゴリズムVは、c0=H(r1,e0+Gx(t0,r1))の等号が成り立つか否かを検証する。次いで、検証者アルゴリズムVは、c3=H(t0,e0)の等号が成り立つか否かを検証する。検証者アルゴリズムVは、これらの検証が全て成功した場合に認証成功を示す値1を出力し、検証に失敗があった場合に認証失敗を示す値0を出力する。
【0118】
Ch=3の場合、検証者アルゴリズムVは、c0=H(r1,y−F(r1)−e1−Gx(t1,r1))の等号が成り立つか否かを検証する。次いで、検証者アルゴリズムVは、c1=H(t1,r1−u1)の等号が成り立つか否かを検証する。次いで、検証者アルゴリズムVは、c4=H(u1,e1)の等号が成り立つか否かを検証する。検証者アルゴリズムVは、これらの検証が全て成功した場合に認証成功を示す値1を出力し、検証に失敗があった場合に認証失敗を示す値0を出力する。
【0119】
以上、3パス方式に係る拡張アルゴリズムの構成例について説明した。3次多項式を利用していることにより、より高い安全性が実現されている。
【0120】
<3:5パスの公開鍵認証方式に係るアルゴリズムの構成>
次に、5パスの公開鍵認証方式に係るアルゴリズムについて説明する。なお、以下の説明において、5パスの公開鍵認証方式のことを「5パス方式」と呼ぶ場合がある。
【0121】
3パス方式の場合には対話プロトコル1回当たりの偽証確率が2/3であったが、5パス方式の場合には対話プロトコル1回当たりの偽証確率が1/2+1/qとなる。但し、qは、利用する環の位数である。従って、環の位数が十分に大きい場合、5パス方式の方が1回当たりの偽証確率を低減することが可能になり、少ない対話プロトコルの実行回数で、偽証確率を十分に小さくすることができる。
【0122】
例えば、偽証確率を1/2n以下にしたい場合、3パス方式においては、n/(log3−1)=1.701n回以上、対話プロトコルを実行する必要がある。一方、偽証確率を1/2n以下にしたい場合、5パス方式においては、n/(1−log(1+1/q))回以上、対話プロトコルを実行する必要がある。従って、q=24にすれば、同じセキュリティレベルを実現するのに必要な通信量は、3パス方式に比べ、5パス方式の方が少なくなるのである。
【0123】
[3−1:具体的なアルゴリズムの構成例(図7)]
まず、図7を参照しながら、5パス方式に係る具体的なアルゴリズムの構成例について紹介する。図7は、5パス方式に係る具体的なアルゴリズムの構成について説明するための説明図である。ここでは、公開鍵pkの一部として2次多項式の組(f1(x),…,fm(x))を利用する場合について考える。但し、2次多項式fi(x)は、上記の式(6)のように表現されるものとする。また、ベクトル(x1,…,xn)をxと表記し、2次多項式の組(f1(x),…,fm(x))を多変数多項式F(x)と表記することにする。
【0124】
3パス方式に係るアルゴリズムと同様、2つのベクトルt0∈Kn、e0∈Kmを用いて、多変数多項式F(x+r0)をマスクするために用いた多変数多項式F1(x)をF1(x)=G(x、t0)+e0のように表現する。この表現を用いると、多変数多項式F(x+r0)について、下記の式(23)で表現される関係が得られる。
【0125】
【数13】

【0126】
そのため、t1=ChA・r0+t0、e1=ChA・F(r0)+e0とすれば、マスク後の多変数多項式F2(x)=ChA・F(x+r0)+F1(x)も、2つのベクトルt1∈Kn、e1∈Kmにより表現することができる。これらの理由から、F1(x)=G(x,t0)+e0と設定すれば、Kn上のベクトル及びKm上のベクトルを用いてF1及びF2を表現できるようになり、通信に必要なデータサイズが少ない効率的なアルゴリズムを実現することが可能になる。
【0127】
なお、F2(或いはF1)からr0に関する情報が一切漏れることはない。例えば、e1及びt1(或いはe0及びt0)を与えられても、e0及びt0(或いはe1及びt1)を知らない限り、r0の情報を一切知ることはできない。従って、零知識性は担保される。以下、上記の論理に基づいて構築された5パス方式のアルゴリズムについて説明する。ここで説明する5パス方式のアルゴリズムは、以下のような鍵生成アルゴリズムGen、証明者アルゴリズムP、検証者アルゴリズムVにより構成される。
【0128】
(鍵生成アルゴリズムGen)
鍵生成アルゴリズムGenは、環K上で定義される多変数多項式f1(x1,…,xn),…,fm(x1,…,xn)、及びベクトルs=(s1,…,sn)∈Knを生成する。次に、鍵生成アルゴリズムGenは、y=(y1,…,ym)←(f1(s),…,fm(s))を計算する。そして、鍵生成アルゴリズムGenは、(f1,…,fm,y)を公開鍵pkに設定し、sを秘密鍵に設定する。なお、以下では、ベクトル(x1,…,xn)をxと表記し、多変数多項式の組(f1(x),…,fm(x))をF(x)と表記する。
【0129】
(証明者アルゴリズムP、検証者アルゴリズムV)
以下、図7を参照しながら、対話プロトコルの中で証明者アルゴリズムP及び検証者アルゴリズムVにより実行される処理について説明する。この対話プロトコルの中で、証明者は、秘密鍵sの情報を検証者に一切漏らさずに、「自身がy=F(s)を満たすsを知っていること」を検証者に示す。一方、検証者は、証明者がy=F(s)を満たすsを知っているか否かを検証する。なお、公開鍵pkは、検証者に公開されているものとする。また、秘密鍵sは、証明者により秘密に管理されているものとする。以下、図7に示したフローチャートに沿って説明を進める。
【0130】
工程#1:
図7に示すように、まず、証明者アルゴリズムPは、ランダムにベクトルr0∈Kn、t0∈Kn、e0∈Kmを生成する。次いで、証明者アルゴリズムPは、r1←s−r0を計算する。この計算は、秘密鍵sをベクトルr0によりマスクする操作に相当する。次いで、証明者アルゴリズムPは、ベクトルr0,t0,e0のハッシュ値c0を生成する。つまり、証明者アルゴリズムPは、c0←H(r0,t0,e0)を計算する。次いで、証明者アルゴリズムPは、G(t0,r1)+e0及びr1のハッシュ値c1を生成する。つまり、証明者アルゴリズムPは、c0←H(r1,G(t0,r1)+e0)を計算する。工程#1で生成されたメッセージ(c0,c1)は、検証者アルゴリズムVに送られる。
【0131】
工程#2:
メッセージ(c0,c1)を受け取った検証者アルゴリズムVは、q通り存在する環Kの元からランダムに1つの数ChAを選択し、選択した数ChAを証明者アルゴリズムPに送る。
【0132】
工程#3:
数ChAを受け取った証明者アルゴリズムPは、t1←ChA・r0−t0を計算する。さらに、証明者アルゴリズムPは、e1←ChA・F(r0)−e0を計算する。そして、証明者アルゴリズムPは、t1及びe1を検証者アルゴリズムVに送る。
【0133】
工程#4:
t1及びe1を受け取った検証者アルゴリズムVは、2つの検証パターンのうち、どちらの検証パターンを利用するかを選択する。例えば、検証者アルゴリズムVは、検証パターンの種類を表す2つの数値{0,1}の中から1つの数値を選択し、選択した数値を要求ChBに設定する。この要求ChBは証明者アルゴリズムPに送られる。
【0134】
工程#5:
要求ChBを受け取った証明者アルゴリズムPは、受け取った要求ChBに応じて検証者アルゴリズムVに送り返す返答Rspを生成する。ChB=0の場合、証明者アルゴリズムPは、返答Rsp=r0を生成する。ChB=1の場合、証明者アルゴリズムPは、返答Rsp=r1を生成する。工程#5で生成された返答Rspは、検証者アルゴリズムVに送られる。
【0135】
工程#6:
返答Rspを受け取った検証者アルゴリズムVは、受け取った返答Rspを利用して以下の検証処理を実行する。
【0136】
ChB=0の場合、検証者アルゴリズムVは、r0←Rspを実行する。そして、検証者アルゴリズムVは、c0=H(r0,ChA・r0−t1,ChA・F(r0)−e1)の等号が成り立つか否かを検証する。検証者アルゴリズムVは、この検証が成功した場合に認証成功を示す値1を出力し、検証に失敗があった場合に認証失敗を示す値0を出力する。
【0137】
ChB=1の場合、検証者アルゴリズムVは、r1←Rspを実行する。そして、検証者アルゴリズムVは、c1=H1(r1,ChA・(y−F(r1))−G(t1,r1)−e1)の等号が成り立つか否かを検証する。検証者アルゴリズムVは、この検証が成功した場合に認証成功を示す値1を出力し、検証に失敗があった場合に認証失敗を示す値0を出力する。
【0138】
以上、5パス方式に係る効率的なアルゴリズムの構成例について説明した。
【0139】
[3−2:並列化アルゴリズムの構成例(図8)]
次に、図8を参照しながら、図7に示した5パス方式のアルゴリズムを並列化する方法について説明する。なお、鍵生成アルゴリズムGenの構成については説明を省略する。
【0140】
先に述べた通り、5パス方式に係る対話プロトコルを適用すれば、偽証が成功する確率を(1/2+1/q)以下に抑制することができる。従って、この対話プロトコルを2回実行すれば、偽証が成功する確率を(1/2+1/q)2以下に抑制することができる。さらに、この対話プロトコルをN回実行すると、偽証が成功する確率は(1/2+1/q)Nとなり、Nを十分に大きい数(例えば、N=80)にすれば、偽証が成功する確率は無視できる程度に小さくなる。
【0141】
対話プロトコルを複数回実行する方法としては、例えば、メッセージ、要求、返答のやり取りを逐次的に複数回繰り返す直列的な方法と、1回分のやり取りで複数回分のメッセージ、要求、返答のやり取りを行う並列的な方法とが考えられる。さらに、直列的な方法と並列的な方法とを組み合わせたハイブリッド型の方法も考えられる。ここでは、5パス方式に係る上記の対話プロトコルを並列的に実行するアルゴリズム(以下、並列化アルゴリズム)について説明する。
【0142】
工程#1:
図8に示すように、まず、証明者アルゴリズムPは、i=1〜Nについて処理(1)〜処理(4)を実行する。
処理(1):証明者アルゴリズムPは、ランダムにベクトルr0i,t0i∈Kn及びe0i∈Kmを生成する。
処理(2):証明者アルゴリズムPは、r1i←s−r0iを計算する。この計算は、秘密鍵sをベクトルr0iによりマスクする操作に相当する。
処理(3):証明者アルゴリズムPは、c0i←H(r0i,t0i,e0i)を計算する。
処理(4):証明者アルゴリズムPは、c1i←H(r1i,G(t0i,r1i)+e0i)を計算する。
i=1〜Nについて処理(1)〜処理(4)を実行した後、証明者アルゴリズムPは、ハッシュ値Cmt←H(c01,c11,…,c0N,c1N)を実行する。そして、工程#1で生成されたハッシュ値Cmtは、検証者アルゴリズムVに送られる。
【0143】
工程#2:
ハッシュ値Cmtを受け取った検証者アルゴリズムVは、i=1〜Nのそれぞれについて、q通り存在する環Kの元からランダムに1つの数ChAiを選択し、選択した数ChAi(i=1〜N)を証明者アルゴリズムPに送る。
【0144】
工程#3:
数ChAi(i=1〜N)を受け取った証明者アルゴリズムPは、i=1〜Nのそれぞれについて、t1i←ChAi・r0i−t0iを計算する。さらに、証明者アルゴリズムPは、i=1〜Nのそれぞれについて、e1i←ChAi・F(r0i)−e0iを計算する。次いで、証明者アルゴリズムPは、ハッシュ値d←H(t11,e11,…,t1N,e1N)を計算する。そして、証明者アルゴリズムPは、ハッシュ値dを検証者アルゴリズムVに送る。
【0145】
工程#4:
ハッシュ値dを受け取った検証者アルゴリズムVは、i=1〜Nのそれぞれについて、2つの検証パターンのうち、どちらの検証パターンを利用するかを選択する。例えば、検証者アルゴリズムVは、検証パターンの種類を表す2つの数値{0,1}の中から1つの数値を選択し、選択した数値を要求ChBiに設定する。要求ChBi(i=1〜N)は証明者アルゴリズムPに送られる。
【0146】
工程#5:
要求ChBi(i=1〜N)を受け取った証明者アルゴリズムPは、i=1〜Nについて、受け取った要求ChBiに応じて検証者アルゴリズムVに送り返す返答Rspiを生成する。ChBi=0の場合、証明者アルゴリズムPは、返答Rspi=(r0i,t0i,e0i,c1i)を生成する。ChBi=1の場合、証明者アルゴリズムPは、返答Rspi=(r1i,t1i,e1i,c0i)を生成する。工程#5で生成された返答Rspi(i=1〜N)は、検証者アルゴリズムVに送られる。
【0147】
工程#6:
返答Rspi(i=1〜N)を受け取った検証者アルゴリズムVは、受け取った返答Rspi(i=1〜N)を利用して以下の処理(1)及び処理(2)を実行する。
【0148】
処理(1):ChBi=0の場合、検証者アルゴリズムVは、(r0i,t0i,e0i,c1i)←Rspiを実行する。そして、検証者アルゴリズムVは、c0i=H(r0i,t0i,e0i)を計算する。さらに、検証者アルゴリズムVは、t1i←ChAi・r0i+t0i、及びe1i←ChAi・F(r0i)−e0iを計算する。そして、検証者アルゴリズムVは、(c0i,c1i,t1i,e1i)を保持する。
【0149】
処理(2):ChBi=1の場合、検証者アルゴリズムVは、(r1i,t1i,e1i,c0i)←Rspiを実行する。そして、検証者アルゴリズムVは、c1i=H(r1i,ChAi・(y−F(r1i))−G(t1i,r1i)−e1i)を計算する。そして、検証者アルゴリズムVは、(c0i,c1i,t1i,e1i)を保持する。
【0150】
i=1〜Nについて処理(1)及び処理(2)を実行した後、検証者アルゴリズムVは、Cmt=H(c01,c11,…,c0N,c1N)の等号が成り立つか否かを検証する。さらに、検証者アルゴリズムVは、d=H(t11,e11,…,t1N,e1N)の等号が成り立つか否かを検証する。そして、検証者アルゴリズムVは、これらの検証が全て成功した場合に認証成功を示す値1を出力し、検証に失敗があった場合に認証失敗を示す値0を出力する。
【0151】
以上、5パス方式に係る効率的な並列化アルゴリズムの構成例について説明した。
【0152】
[3−3:3次多変数多項式に基づくアルゴリズムの構成例]
さて、3パス方式の場合と同様、環R上の3次多項式flを利用した効率的なアルゴリズムの構築方法について検討してみたい。3次多項式flを上記の式(12)のように表現した場合に、Gx(x,y)及びGy(x,y)がx及びyについて線形になることについては式(14)と式(15)より分かる。
【0153】
そこで、上記の性質を利用し、新たな変数r0,r1,t0,u0,e0を導入して、公開鍵F(s)をChA倍した項を分割する。多項式Gx,Gyがそれぞれxとyについて線形であるから、変数r0,r1,t0,u0,e0を用いて、下記の式(24)〜式(27)の関係が成り立つ。また、下記の式(24)〜式(27)は、ChAに依存する第1の部分と、ChAに依存しない第2の部分とに分けることができる。但し、第1の部分は、(r1,t1,u1,e1)で再現可能である。また、第2の部分は、(r0,t1,u1,e1)で再現可能である。
【0154】
例えば、下記の式(32)に含まれる「e0,Gx(t0,r1)」、下記の式(33)に含まれる「t0」、下記の式(26)に含まれる「u0」、下記の式(27)に含まれる「e0,Gy(r0,u0)」は第1の部分である。一方、下記の式(24)に含まれる「ChA・F(r0+r1),e1,ChA・F(r1),Gx(t1,r1)」、下記の式(25)に含まれる「ChA・r0,t1」、下記の式(34)に含まれる「ChA・r1,u1」、下記の式(27)に含まれる「ChA・F(r0),Gy(r0,u1),e1」は第2の部分である。
【0155】
また、秘密鍵sの定義及び下記の式(24)〜式(27)の関係から、(r1,t1,u1,e1)、(r0,t1,u1,e1)のいずれか1つを用いても秘密鍵sは得られないことが保証される。これらの性質を利用すると、例えば、環R上の3次多項式flを利用した効率的なアルゴリズム(以下、拡張アルゴリズム)を構築することができる。
【0156】
【数14】

【0157】
以下、具体的な拡張アルゴリズムの構成例について説明する。拡張アルゴリズムの設計に関する基本的なポイントは、下記の式(28)及び式(29)で表現されるメッセージを検証者に送ること、及び検証者が選択したChAについて、ChAに依存する部分(第1の部分)に関する検証を行うことの2点である。但し、「メッセージを生成する際に利用したr0及びr1を、検証の際に別のr0及びr1にすり替えられることを防ぐ」ために、r0及びr1に関する検証を追加した構成例を以下で紹介する。
【0158】
【数15】

【0159】
以下、図9を参照しながら、5パス方式に係る拡張アルゴリズムの基本構成について説明する。なお、鍵生成アルゴリズムGenの構成については説明を省略する。
【0160】
工程#1:
図9に示すように、証明者アルゴリズムPは、ランダムにベクトルr0,t0,u0∈Kn及びe0∈Kmを生成する。次いで、証明者アルゴリズムPは、r1←s−r0を計算する。この計算は、秘密鍵sをベクトルr0によりマスクする操作に相当する。次いで、証明者アルゴリズムPは、c0←H(r0,t0,e0−Gy(r0,u0))を計算する。次いで、証明者アルゴリズムPは、c1←H(r1,u0,Gx(t0,r1)+e0)を計算する。工程#1で生成されたメッセージ(c0,c1)は、検証者アルゴリズムVに送られる。
【0161】
工程#2:
メッセージ(c0,c1)を受け取った検証者アルゴリズムVは、ランダムに数ChAを選択する。この数ChAは証明者アルゴリズムPに送られる。
【0162】
工程#3:
数ChAを受け取った証明者アルゴリズムPは、t1←ChA・r0−t0を計算する。次いで、証明者アルゴリズムPは、u1←ChA・r1−u0を計算する。次いで、証明者アルゴリズムPは、e1←ChA・F(r0)+ChA・Gy(r0,r1)−e0を計算する。工程#3で生成された(t1,u1,e1)は、検証者アルゴリズムVに送られる。
【0163】
工程#4:
(t1,u1,e1)を受け取った検証者アルゴリズムVは、2つの検証パターンのうち、どの検証パターンを利用するかを選択する。例えば、検証者アルゴリズムVは、検証パターンの種類を表す2つの数値{0,1}の中から1つの数値を選択し、選択した数値を要求ChBに設定する。この要求ChBは証明者アルゴリズムPに送られる。
【0164】
工程#5:
要求ChBを受け取った証明者アルゴリズムPは、受け取った要求ChBに応じて検証者アルゴリズムVに送る返答Rspを生成する。ChB=0の場合、証明者アルゴリズムPは、返答Rsp=r0を生成する。ChB=1の場合、証明者アルゴリズムPは、返答Rsp=r1を生成する。工程#5で生成された返答Rspは、検証者アルゴリズムVに送られる。
【0165】
工程#6:
返答Rspを受け取った検証者アルゴリズムVは、受け取った返答Rspを利用して以下の検証処理を実行する。
【0166】
ChB=0の場合、検証者アルゴリズムVは、c0=H(r0,ChA・r0−t1,ChA・F(r0)+Gy(r0,u1)−e1)の等号が成り立つか否かを検証する。検証者アルゴリズムVは、この検証が成功した場合に認証成功を示す値1を出力し、検証に失敗があった場合に認証失敗を示す値0を出力する。
【0167】
ChB=1の場合、検証者アルゴリズムVは、c1=H(r1,ChA・r1−u1,ChA・(y−F(r1))−Gx(t1,r1)−e1)の等号が成り立つか否かを検証する。検証者アルゴリズムVは、この検証が成功した場合に認証成功を示す値1を出力し、検証に失敗があった場合に認証失敗を示す値0を出力する。
【0168】
以上、5パス方式に係る拡張アルゴリズムの構成例について説明した。3次多項式を利用していることにより、より高い安全性が実現される。
【0169】
<4:電子署名方式への変形>
次に、上記の公開鍵認証方式を電子署名方式へと変形する方法を紹介する。
【0170】
公開鍵認証方式のモデルにおける証明者を電子署名方式における署名者に対応させると、証明者のみが検証者を納得させられるという点において、電子署名方式のモデルと近似していることが容易に理解されよう。こうした考えに基づき、上述した公開鍵認証方式を電子署名方式へと変形する方法について説明する。
【0171】
[4−1:3パスの公開鍵認証方式から電子署名方式への変形(図10)]
まず、3パスの公開鍵認証方式から電子署名方式への変形について説明する。
【0172】
図10に示すように、3パス方式に係る効率的なアルゴリズム(例えば、図5を参照)は、3回の対話及び4つの工程#1〜工程#4で表現される。
【0173】
工程#1は、i=1〜Nについて、ai=(r0i,t0i,e0i,r1i,t1i,e1i,c0i,c1i,c2i)を生成する処理(1)と、Cmt←H(c01,c11,c21,…,c0N,c1N,c2N)を計算する処理(2)とで構成される。工程#1で証明者アルゴリズムPにより生成されたCmtは、検証者アルゴリズムVへと送られる。
【0174】
工程#2は、Ch1,…,ChNを選択する処理で構成される。工程#2で検証者アルゴリズムVにより選択されたCh1,…,ChNは、証明者アルゴリズムPへと送られる。
【0175】
工程#3は、Ch1,…,ChN及びa1,…,aNを用いてRsp1,…,RspNを生成する処理で構成される。この処理をRspi←Select(Chi,ai)と表現する。工程#3で証明者アルゴリズムPにより生成されたRsp1,…,RspNは、検証者アルゴリズムVへと送られる。
【0176】
工程#4は、Ch1,…,ChN及びRsp1,…,RspNを用いてc01,c11,c21,…,c0N,c1N,c2Nを再生する処理(1)と、再生したc01,c11,c21,…,c0N,c1N,c2Nを用いてCmt=H(c01,c11,c21,…,c0N,c1N,c2N)を検証する処理(2)とで構成される。
【0177】
上記の工程#1〜工程#4で表現される公開鍵認証方式のアルゴリズムは、図10に示すような署名生成アルゴリズムSig及び署名検証アルゴリズムVerに変形される。
【0178】
(署名生成アルゴリズムSig)
まず、署名生成アルゴリズムSigの構成について述べる。署名生成アルゴリズムSigは、以下の処理(1)〜処理(5)で構成される。
【0179】
処理(1):署名生成アルゴリズムSigは、ai=(r0i,t0i,e0i,r1i,t1i,e1i,c0i,c1i,c2i)を生成する。
処理(2):署名生成アルゴリズムSigは、Cmt←H(c01,c11,c21,…,c0N,c1N,c2N)を計算する。
処理(3):署名生成アルゴリズムSigは、(Ch1,…,ChN)←H(M,Cmt)を計算する。このMは、署名を付与する文書である。
処理(4):署名生成アルゴリズムSigは、Rspi←Select(Chi,ai)を計算する。
処理(5):署名生成アルゴリズムSigは、(Cmt,Rsp1,…,RspN)を署名に設定する。
【0180】
(署名検証アルゴリズムVer)
次に、署名検証アルゴリズムVerの構成について述べる。署名検証アルゴリズムVerは、以下の処理(1)〜処理(3)で構成される。
【0181】
処理(1):署名検証アルゴリズムVerは、(Ch1,…,ChN)←H(M,Cmt)を計算する。
処理(2):署名検証アルゴリズムVerは、Ch1,…,ChN及びRsp1,…,RspNを用いてc01,c11,c21,…,c0N,c1N,c2Nを生成する。
処理(3):署名検証アルゴリズムVerは、再生したc01,c11,c21,…,c0N,c1N,c2Nを用いてCmt=H(c01,c11,c21,…,c0N,c1N,c2N)を検証する。
【0182】
以上説明したように、公開鍵認証方式のモデルにおける証明者を電子署名方式における署名者に対応させることで、公開鍵認証方式のアルゴリズムを電子署名方式のアルゴリズムへと変形することが可能になる。
【0183】
[4−2:5パスの公開鍵認証方式から電子署名方式への変形(図11)]
次に、5パスの公開鍵認証方式から電子署名方式への変形について説明する。
【0184】
図11に示すように、5パス方式に係る効率的なアルゴリズム(例えば、図8を参照)は、5回の対話及び6つの工程#1〜工程#6で表現される。
【0185】
工程#1は、i=1〜Nについて、ai=(r0i,t0i,e0i,r1i,t1i,e1i,c0i,c1i)を生成する処理(1)と、Cmt←H(c01,c11,…,c0N,c1N)を計算する処理(2)とで構成される。工程#1で証明者アルゴリズムPにより生成されたCmtは、検証者アルゴリズムVへと送られる。
【0186】
工程#2は、ChA1,…,ChANを選択する処理で構成される。工程#2で検証者アルゴリズムVにより選択されたChA1,…,ChANは、証明者アルゴリズムPへと送られる。
【0187】
工程#3は、i=1〜Nについて、bi=(t1i,e1i)を生成する処理、及びd=H(t11,e11,…,t1N,e1N)を生成する処理で構成される。工程#3で証明者アルゴリズムPにより生成されたdは、検証者アルゴリズムVへと送られる。
【0188】
工程#4は、ChB1,…,ChBNを選択する処理で構成される。工程#4で検証者アルゴリズムVにより選択されたChB1,…,ChBNは、証明者アルゴリズムPへと送られる。
【0189】
工程#5は、ChB1,…,ChBN,a1,…,aN,b1,…,bNを用いてRsp1,…,RspNを生成する処理で構成される。この処理をRspi←Select(ChBi,ai,bi)と表現する。工程#5で証明者アルゴリズムPにより生成されたRsp1,…,RspNは、検証者アルゴリズムVへと送られる。
【0190】
工程#6は、ChA1,…,ChAN,ChB1,…,ChBN,Rsp1,…,RspNを用いてc01,c11,…,c0N,c1N,t11,e11,…,t1N,e1Nを再生する処理と、再生したc01,c11,…,c0N,c1Nを用いてCmt=H(c01,c11,…,c0N,c1N)を検証する処理と、d=H(t11,e11,…,t1N,e1N)を検証する処理とで構成される。
【0191】
上記の工程#1〜工程#6で表現される公開鍵認証方式のアルゴリズムは、図11に示すような署名生成アルゴリズムSig及び署名検証アルゴリズムVerに変形される。
【0192】
(署名生成アルゴリズムSig)
まず、署名生成アルゴリズムSigの構成について述べる。署名生成アルゴリズムSigは、以下の処理(1)〜処理(7)で構成される。
【0193】
処理(1):署名生成アルゴリズムSigは、ai=(r0i,t0i,e0i,r1i,t1i,e1i,c0i,c1i)を生成する。
処理(2):署名生成アルゴリズムSigは、Cmt←H(c01,c11,…,c0N,c1N)を計算する。
処理(3):署名生成アルゴリズムSigは、(ChA1,…,ChAN)←H(M,Cmt)を計算する。このMは、署名を付与する文書である。
処理(4):署名生成アルゴリズムSigは、i=1〜Nについて、bi=(t1i,e1i)を生成する。さらに、署名生成アルゴリズムSigは、d=H(t11,e11,…,t1N,e1N)を算出する。
処理(5):署名生成アルゴリズムSigは、(ChB1,…,ChBN)←H(M,Cmt,ChA1,…,ChAN,d)を計算する。なお、(ChB1,…,ChBN)←H(ChA1,…,ChAN,d)と変形してもよい。
処理(6):署名生成アルゴリズムSigは、Rspi←Select(ChBi,ai,bi)を計算する。
処理(7):署名生成アルゴリズムSigは、(Cmt,d,Rsp1,…,RspN)を電子署名に設定する。
【0194】
(署名検証アルゴリズムVer)
次に、署名検証アルゴリズムVerの構成について述べる。署名検証アルゴリズムVerは、以下の処理(1)〜処理(4)で構成される。
【0195】
処理(1):署名検証アルゴリズムVerは、(ChA1,…,ChAN)←H(M,Cmt)を計算する。
処理(2):署名検証アルゴリズムVerは、(ChB1,…,ChBN)←H(M,Cmt,ChA1,…,ChAN,d)を計算する。なお、署名検証アルゴリズムVerが実行する処理(5)において、(ChB1,…,ChBN)←H(ChA1,…,ChAN,d)と変形した場合、署名検証アルゴリズムVerは、(ChB1,…,ChBN)←H(ChA1,…,ChAN,d)を計算する。
処理(3):署名検証アルゴリズムVerは、ChA1,…,ChAN,ChB1,…,ChBN,Rsp1,…,RspNを用いてt11,e11,…,t1N,e1N,c01,c11,…,c0N,c1Nを生成する。
処理(4):署名検証アルゴリズムVerは、再生したc01,c11,…,c0N,c1Nを用いてCmt=H(c01,c11,…,c0N,c1N)及びd=H(t11,e11,…,t1N,e1N,)を検証する。
【0196】
以上説明したように、公開鍵認証方式のモデルにおける証明者を電子署名方式における署名者に対応させることで、公開鍵認証方式のアルゴリズムを電子署名方式のアルゴリズムへと変形することが可能になる。
【0197】
<5:署名検証に要するメモリ量の削減方法について>
ところで、上述した電子署名方式のアルゴリズムにおいては、署名検証アルゴリズムVerが電子署名全体を受信した後で署名検証の処理を実行していた。しかし、上述した電子署名方式の場合、電子署名のデータサイズが比較的大きい。そのため、RFID(Radio Frequency IDentification)など、少ないメモリ容量しか持たないデバイスを用いて認証を行う場合には、メモリの空き容量や認証処理中のメモリ使用率などに気を配る必要があった。また、十分なメモリ容量を持たないデバイスを利用する場合、認証を行うことができない場合も想定される。そこで、本件発明者は、署名検証に要するメモリ量の削減方法を考案した。
【0198】
[5−1:ハッシュ関数の構造について(図12)]
まず、本件発明者は、ハッシュ関数の構造に注目した。多くの場合、ハッシュ関数は、入力をブロック単位に区切り、ブロック単位で順次処理を進める構造を有している。例えば、SHA−1の場合、ハッシュ関数は、図12に示すような構造を有している。図12に示すハッシュ関数は、パディング済みの入力MをZ個のブロックm1,…,mZに区切り、インデックスjをインクリメントしながら、逐次的に、ブロックmjを初期値IV又は中間値CVjと共に所定の関数CFに作用させてハッシュ値を生成する。従って、中間値CVjが得られた時点で、それ以前に利用したブロックは不要になる。そこで、この特性を利用し、アルゴリズムの実行に必要なメモリ量を効果的に削減する仕組み(以下、メモリ削減方法)を考案した。以下、この仕組みを上述した電子署名方式に適用する方法について説明する。
【0199】
[5−2:3パス方式に基づく電子署名方式への適用例(図14)]
まず、図10に示した3パス方式に基づく電子署名方式のアルゴリズムに上記のメモリ削減方法を適用する方法について説明する。
【0200】
(通常の実装方法:図13)
通常、上述した電子署名方式に係る署名検証アルゴリズムVerは、図13に示すように、電子署名を構成する(Cmt,Rsp1,…,RspN)を1度に受信する(S101)。次いで、署名検証アルゴリズムVerは、(Ch1,…,ChN)←H(M,Cmt)を実行する(S102)。次いで、署名検証アルゴリズムVerは、(c01,c11,c21,…,c0N,c1N,c2N)←Reproduce(Ch1,…,ChN;Rsp1,…,RspN)を実行する(S103)。次いで、署名検証アルゴリズムVerは、Cmt=H(c01,c11,c21,…,c0N,c1N,c2N)を検証し(S104)、署名検証に係る一連の処理を終了する。
【0201】
(メモリ削減方法:図14)
通常の実装方法の場合、図13のステップS101のように、一度に電子署名を受信すると、ステップS103の処理が完了するまで(Rsp1,…,RspN)を保持しておくためのメモリが必要になる。しかし、図5のアルゴリズム構成から分かるように、ステップS103で実行する(c0i,c1i,c2i)の再生には(Chi;Rspi)以外の情報を利用しない。また、図12に示したハッシュ関数の構造を考慮すると、ステップS104において実行されるハッシュ関数の計算はブロック単位で分割して実行できることが分かる。そこで、署名検証に係る処理の構成を図14に示すような構成に改良する。
【0202】
図14に示す構成の場合、署名検証アルゴリズムVerは、まず、電子署名に含まれるCmtだけを受信する(S111)。次いで、署名検証アルゴリズムVerは、(Ch1,…,ChN)←H(M,Cmt)を実行する(S112)。次いで、署名検証アルゴリズムVerは、i=1〜Nについて、iをインクリメントさせながら逐次的にステップS113〜S115の処理を実行する。
【0203】
ステップS113において、署名検証アルゴリズムVerは、Rspiを受信する(S113)。次いで、署名検証アルゴリズムVerは、受信したRspiを用いて、(c0i,c1i,c2i)←Reproduce(Chi;Rspi)を実行する(S114)。ステップS114の処理を実行した後、Chi及びRspiは不要になる。そこで、署名検証アルゴリズムVerは、ステップS114の処理を実行後にChi及びRspiをメモリから消去する。
【0204】
次いで、署名検証アルゴリズムVerは、tmpi←Hi(tmpi−1;c0i,c1i,c2i)を実行する(S115)。なお、関数Hiは、ハッシュ関数Hの内部でc0i,c1i,c2iまで計算した際に生成される中間値を出力する関数である。実際には選択したハッシュ関数に応じて関数Hiの入力サイズは異なるため必要に応じて、ビットを付加するなどの適切な入力長の補正が行われる。関数Hiを用いると、ハッシュ関数Hは、以下に示す処理(1)〜処理(3)で構成されたアルゴリズムにより表現される。そして、tmpNがハッシュ関数Hの最終的な出力(ハッシュ値)となる。実際にはハッシュ関数の仕様に応じて、最終処理においてパディングの追加処理を行う。
【0205】
処理(1):tmp0←空文字列
処理(2):
for i=1 to N
tmpi←Hi(tmpi−1;c0i,c1i,c2i)
end for
処理(3):output tmpN
【0206】
i=1〜Nについて、ステップS113〜S115の処理を実行した後、署名検証アルゴリズムVerは、Cmt=tmpNが成り立つか否かを検証し(S116)、署名検証に係る一連の処理を終了する。上記のように、署名検証アルゴリズムVerは、ステップS113〜S115の処理を繰り返し実行する過程で不要になった情報をメモリかた消去する。そのため、署名検証に要するメモリ量は最小限に抑えられる。その結果、少ないメモリ容量しか持たないデバイスでも、上記の署名検証が可能になる。
【0207】
[5−3:5パス方式に基づく電子署名方式への適用例(図16)]
次に、図11に示した5パス方式に基づく電子署名方式のアルゴリズムに上記のメモリ削減方法を適用する方法について説明する。
【0208】
(通常の実装方法:図15)
通常、上述した電子署名方式に係る署名検証アルゴリズムVerは、図15に示すように、電子署名を構成する(Cmt,d,Rsp1,…,RspN)を1度に受信する(S121)。次いで、署名検証アルゴリズムVerは、(ChA1,…,ChAN)←H(M,Cmt)を実行する(S122)。次いで、署名検証アルゴリズムVerは、(ChB1,…,ChBN)←H(M,Cmt,ChA1,…,ChAN,d)を実行する(S123)。次いで、署名検証アルゴリズムVerは、(c01,c11,…,c0N,c1N,d11,e11,…,d1N,e1N)←Reproduce(ChA1,…,ChAN,ChB1,…,ChBN;Rsp1,…,RspN)を実行する(S124)。次いで、署名検証アルゴリズムVerは、Cmt=H(c01,c11,…,c0N,c1N)とd=H(d11,e11,…,d1N,e1N)を検証し(S125)、署名検証に係る一連の処理を終了する。
【0209】
(メモリ削減方法:図16)
図15のステップS121のように、一度に電子署名を受信すると、ステップS124の処理が完了するまで(Rsp1,…,RspN)を保持しておくためのメモリが必要になる。しかしながら、図8のアルゴリズム構成から分かるように、ステップS124で実行する(c0i,c1i,d1i,e1i)の再生には(ChAi,ChBi;Rspi)以外の情報を利用しない。また、図12に示したハッシュ関数の構造を考慮すると、ステップS125において実行されるハッシュ関数の計算はブロック単位で分割して実行できることが分かる。そこで、署名検証に係る処理の構成を図16に示すような構成に改良する。
【0210】
図16に示す構成の場合、署名検証アルゴリズムVerは、まず、電子署名に含まれるCmtだけを受信する(S131)。次いで、署名検証アルゴリズムVerは、(ChA1,…,ChAN)←H(M,Cmt)を実行する(S132)。
【0211】
次いで、署名検証アルゴリズムVerは、dを受信する(S133)。次いで、署名検証アルゴリズムVerは、受信したdを用いて、(ChB1,…,ChBN)←H(M,Cmt,ChA1,…,ChAN,d)を実行する(S134)。ステップS134の処理を実行した後、dは不要になる。そこで、署名検証アルゴリズムVerは、ステップS134の処理を実行後にdをメモリから消去する。次いで、署名検証アルゴリズムVerは、i=1〜Nについて、iをインクリメントさせながら逐次的にステップS135〜S137の処理を実行する。
【0212】
ステップS135において、署名検証アルゴリズムVerは、Rspiを受信する(S135)。次いで、署名検証アルゴリズムVerは、受信したRspiを用いて、(c0i,c1i,t1i,e1i)←Reproduce(ChAi,ChBi,Rspi)を実行する(S136)。ステップS136の処理を実行した後、ChAi、ChBi及びRspiは不要になる。そこで、署名検証アルゴリズムVerは、ステップS136の処理を実行後にChAi、ChBi及びRspiをメモリから消去する。
【0213】
次いで、署名検証アルゴリズムVerは、tmpi←Hi(tmpi−1;c0i,c1i)とtmpi’←Hi(tmpi−1’;t1i,e1i)を実行する(S137)。i=1〜Nについて、ステップS135〜S137の処理を実行した後、署名検証アルゴリズムVerは、Cmt=tmpNとd=tmpN’が成り立つか否かを検証し(S138)、署名検証に係る一連の処理を終了する。上記のように、署名検証アルゴリズムVerは、ステップS135〜S137の処理を繰り返し実行する過程で不要になった情報をメモリから消去する。そのため、署名検証に要するメモリ量は最小限に抑えられる。その結果、少ないメモリ容量しか持たないデバイスでも、上記の署名検証が可能になる。
【0214】
以上、署名検証に要するメモリ量の削減方法について説明した。
【0215】
<6:2進数の乱数列から3進数の乱数列を抽出する方法について>
ところで、3パス方式に基づく公開鍵認証方式のアルゴリズムにおいて、3進数の一様乱数をN個以上生成する場面が存在する。しかし、3進数の一様乱数を生成する優れた乱数生成器は一般的ではない。そのため、2進数の一様乱数を生成する優れた乱数生成器を用いて3進数の一様乱数を生成する方法を考える必要がある。そこで、本件発明者は、2進数の一様乱数から3進数の一様乱数を効率的に生成する方法を考案した。以下、この方法について詳細に説明する。なお、以下の説明において、l進表現(lは2又は3)で表された1つの数を1シンボルと数えることにする。
【0216】
[6−1:抽出方法#1(2ビット区切り)(図17)]
まず、図17を参照しながら、Mビットの2進数を2ビットずつ区切って3進数を抽出する方法(以下、抽出方法#1)を紹介する。図17に示すように、2進表現の乱数列を2ビットずつ区切ると、M/2個の2ビットの乱数が得られる。例えば、「00」を3進数の「0」、「01」を3進数の「1」、「10」を3進数の「2」に対応付けると、2ビット単位の2進表現の乱数列から3進数の乱数列を得ることができる。但し、2ビットの値「11」は除外する。つまり、抽出方法#1は、2進数2シンボルで表現される22通りの数の中から、3進数1シンボルで表現される31通りの数を抽出する方法である。従って、N個以上の3進数が抽出できない確率P1は、下記の式(30)のようになる。
【0217】
【数16】

【0218】
[6−2:抽出方法#2(区切りなし)(図18)]
次に、図18を参照しながら、2進数Mシンボルの乱数を区切らずに利用して3進数Lシンボルの乱数を抽出する方法(以下、抽出方法#2)を紹介する。但し、Lは、3L≦2Mとなる最大の整数である。2進数Mシンボルで表現可能な数は、2M通り存在する。一方、3進数Lシンボルで表現可能な数は、3L通りしか存在しない。そのため、2進数Mシンボルで表現される2M通りの数のうち、2M−3L通りの数は、3進表現の乱数として利用されない。従って、N個以上の3進数が抽出できない確率P2は、下記の式(31)のようになる。
【0219】
【数17】

【0220】
[6−3:抽出方法#3(kビット区切り)(図19)]
上記の抽出方法#1は、最小の区切り単位で2進表現の乱数列を区切る方法である。一方、上記の抽出方法#2は、(Mビット区切りと考えられるため)最大の区切り単位で2進表現の乱数列を区切る方法である。上記の式(30)及び式(31)から分かるように、区切る長さに応じて、N個以上の3進数が抽出できない確率は異なる。因みに、図19に示すように、kビット単位で2進Mシンボルの乱数列を区切った場合、N個以上の3進数が抽出できない確率P3は、下記の式(32)のようになる。
【0221】
【数18】

【0222】
N個以上の3進数が抽出できない確率P3を最小化することができれば、最も効率よく3進表現の乱数列を抽出できることになる。例えば、M=512、N=140の場合、k=8のときに確率P3が最小となる。
【0223】
(6−3−1:基本構成(図20))
ここで、図20を参照しながら、2進Mシンボルの乱数列から3進Lシンボルの乱数列を抽出する処理の流れについて説明する。図20に示すように、まず、2進Mシンボルの乱数列が生成される(S201)。次いで、2進Mシンボルの乱数列が、kビット単位に区切られる(S202)。次いで、kビット単位で区切られたビット列X2kのうち、X2k≦3Lとなるビット列が抽出される(S203)。次いで、抽出されたビット列が、3進数表現で出力され(S204)、一連の処理が終了する。
【0224】
(6−3−2:追加抽出方法(図21))
上記の式(15)で表現される確率P3が最小となる区切りの長さkを算出し、図20に示したアルゴリズムを実行することにより、2進表現の乱数列から3進表現の乱数列を効率的に抽出することが可能になる。しかし、本件発明者は、図20のステップS204においてX2k>3Lとなるビット列が利用されない点に注目し、3進表現の乱数列をより効率的に抽出する方法を考案した。以下、この方法について、図21を参照しながら説明する。
【0225】
この方法は、図20のステップS204で抽出されなかったビット列を利用して、3進表現のシンボル列を抽出する方法である。図21に示すように、まず、図20のステップS204で抽出されなかった、X2k>3Lとなるビット列の組(例えば、ビット列の組をy1y2…yN’と表現すると、個々のビット列yiは3L≦yi<2k)が抽出される(S211)。次いで、抽出したビット列yiからそれぞれ3Lが減算され、新たなビット列の組(例えば、新たなビット列の組をz1z2…zN’と表現すると、個々のビット列zi=yi−3Lは0≦zi<2k−3L)が算出される(S212)。
【0226】
次いで、新たなビット列の組から、ビット列XがX<3L’となるものが抽出される(S213)。但し、L’は、3L’≦2k−3Lとなる最大の整数である。次いで、ステップS213で抽出されたビット列が3進表現で出力され(S214)、一連の処理が終了する。このアルゴリズムを適用することにより、確率3L’/(2k−3L)で新たにL’個の3進数を抽出することが可能になる。なお、この方法を再帰的に用いることで、さらに多くの3進数を抽出することができる。つまり、ステップS213でビット列XがX≧3L’となったビット列から同様にして3進数を抽出することができる。
【0227】
以上、2進数の一様乱数から3進数の一様乱数を効率的に生成する方法について説明した。
【0228】
<7:多変数多項式の係数を効率的に代入する方法について>
さて、これまでは多変数多項式を証明者(又は署名者)と検証者との間で共有する方法について具体的に明示してこなかった。多変数多項式を共有する方法としては、多変数多項式の係数(乱数)を生成する際に用いるシードを両者で共有する方法が考えられる。しかしながら、共有しているシードを利用して生成した乱数を係数に当てはめる順序を両者で共有しない限り、多変数多項式を共有したことにはならない。
【0229】
[7−1:基本的な取り決め]
そこで、証明者(又は署名者)と検証者との間で、共有しているシードを用いて生成した乱数列を、どの順序で多変数多項式に当てはめるかについて基本的な取り決めを行う。そして、多変数多項式を利用する際に、この基本的な取り決めに従って乱数列を多変数多項式に当てはめる。このような方法を用いれば、証明者(又は署名者)と検証者との間で多変数多項式を共有したことになる。
【0230】
[7−2:データの構造化]
但し、多変数多項式を構成する係数の数は膨大である。1つの係数が1ビット単位で表現されている場合、多変数多項式を表現するのに最低でも数万ビット以上のデータが必要になる。そのため、数を多変数多項式の係数に代入する処理の負荷は非常に高い。そこで、本件発明者は、多変数多項式の係数を所定の単位で構造化し、係数への代入処理を効率化する手法(構造化手法#1及び#2)を考案した。さらに、本件発明者は、同じ多変数多項式の係数に対して複数回の代入処理を実行する場合に、その処理効率を向上させる手法(構造化手法#3)を考案した。以下、これらの手法について詳細に説明する。
【0231】
(7−2−1:構造化手法#1(図22〜図26))
まず、構造化手法#1について説明する。構造化手法#1は、図22及び図23に示すように、多変数多項式を構成する同じ種類の項の係数を1つのデータ構造として纏める手法である。図22の例では、多変数多項式Fの係数a1IJ〜aMIJがデータ構造Aとして纏められ、係数b1I〜bMIがデータ構造Bとして纏められている。また、図23に示すように、多変数多項式Gについても同様の手法が適用可能である。この場合、係数(a1IJ+a1JI)〜(aMIJ+aMJI)がデータ構造として纏められる。
【0232】
構造化手法#1を適用しない場合、M本のN変数多項式で構成される多変数多項式Fの計算は、(例1)に示すようなアルゴリズムにより行われる。(例1)の場合、1ビットのAND演算(&)を2×N×(N+1)×M/2回実行する必要がある。さらに、1ビットのXOR演算(^)を1×N×(N+1)×M/2回実行する必要がある。なお、入力xはNビットであるとする。
【0233】
(例1)
input x;
for L=1 to M
for I=1 to N
for J=I to N
[yのLビット目]^=[aLIJ]&[xのIビット目]&[xのJビット目];
end for
end for
end for
output y;
【0234】
一方、図22に示すように係数を構造化し、生成した乱数を多変数多項式Fの係数として一部ずつ逐次適用していく場合、係数の代入アルゴリズムは(例2)のようになる。(例2)の場合、MビットのAND演算(&)を2×N×(N+1)/2回、MビットのXOR演算(^)をN×(N+1)/2回実行するだけで済む。なお、a(1〜M)IJは、それぞれループのタイミングで生成される。また、係数を使い回してもよい。例えば、N(N−1)/2回のループを実行する際、[a(1〜M)IJ]を毎回生成せず、M回に1回だけ生成するようにしてもよい。また、M回のループ中、[a(1〜M)IJ]を1ビットずつローテーションしながら利用してもよい。
【0235】
(例2)
input x;
for I=1 to N
for J=I to N
[yの1〜Mビット目]^=[a(1〜M)IJ]&[xのIビット目]&[xのJビット目];
end for
end for
output y;
【0236】
また、図22に示すように係数を構造化する場合、多変数多項式Fの係数を適用した中間の結果をテーブルに保持するようにしてもよい。この場合、上記のアルゴリズムは(例3)のようになる。なお、配列aIJ[0][0]〜aIJ[2k−1][2k−1]には、それぞれ、aIJ[x1,…,xk][z1,…,zk]=(a(k(I−1)+1)(k(J−1)+1)&x1&z1)^…^(a(k(I−1)+1)(k(J−1)+k)&x1&zk)^…^(a(k(I−1)+k)(k(J−1)+1)&xk&z1)^…^(a(k(I−1)+k)(k(J−1)+k)&xk&zk)が格納されている。(例3)の場合、MビットのXOR演算(^)を(N/k)(N/k+1)/2回実行するだけで済む。但し、(例2)のアルゴリズムに比べると、必要なメモリ量は、22k/k2倍となる。
【0237】
例えば、k=1のとき、MビットXOR演算が120*119/2=7140回、必要なメモリ量が(例2)の22=4倍、ループ回数は変化なしとなる。また、k=2のとき、MビットXOR演算が60*59/2=1770回、必要なメモリ量が24/4=4倍、ループ回数が1/4となる。k=4のとき、MビットXOR演算が30*29/2=435回、必要なメモリ量が28/42=16倍、ループ回数が1/16.4となる。k=6のとき、MビットXOR演算が20*19/2=190回、必要なメモリ量が212/62=114倍、ループ回数が1/37.6となる。k=8のとき、MビットXOR演算が15*14/2=135回、必要なメモリが216/82=1024倍、ループ回数が1/52.9となる。
【0238】
(例3)
input x;
for I=1 to N/k
for J=I to N/k
[yの1〜Mビット目]^=a(1〜M)IJ[xのk(I−1)+1〜kビット目][xのk(J−1)+1〜kビット目];
end for
end for
output y;
【0239】
なお、(例3)に示した手法は、ちょうど、下記の式(33)で定義されるFIJ(…)の値を予め計算し、配列として保持しておく手法と言える。
【0240】
【数19】

【0241】
以上、構造化手法#1を多変数多項式Fへ適用するケースを例に挙げて具体的なアルゴリズムについて説明した。かかる構成により、アルゴリズムを実行する際に処理の高速化が期待できる。
【0242】
(Gへの適用)
ここまで、図22を参照しながら、構造化手法#1を適用して多変数多項式Fを計算するアルゴリズムについて説明してきた。一方で、多変数多項式Gの各要素も二次形式で表現されることから、図23に示すように、同様にして上記の構造化手法#1を多変数多項式Gの計算にそのまま適用することも可能である。
【0243】
例えば、上記の構造化手法#1を適用しない場合、多変数多項式Gを計算するアルゴリズムは、下記の(例1’)のように表現される。なお、入力x及びyはそれぞれNビットであるとする。
【0244】
(例1’)
input x,y;
for L=1 to M
for I=1 to N
for J=1 to N
[zのLビット目]^=[aLIJ+aLJI]&[xのIビット目]&[yのJビット目];
end for
end for
end for
output z;
【0245】
上記の(例1’)に対し、上述した構造化手法#1を適用すると、多変数多項式Gを計算するアルゴリズムは、下記の(例2’)のようになる。
【0246】
(例2’)
input x,y;
for I=1 to N
for J=1 to N
[zの1〜Mビット目]^=[a(1〜M)IJ+a(1〜M)JI]&[xのIビット目]&[yのJビット目];
end for
end for
output z;
【0247】
また、多変数多項式Gの係数を適用した中間の結果をテーブルに保持する手法の場合、多変数多項式Gを計算するアルゴリズムは、上記の(例3)に対応して下記の(例3’)のようになる。なお、配列aIJ[0][0]〜aIJ[2k−1][2k−1]には、それぞれ、aIJ[x1,…,xk][y1,…,yk]=(a(k(I−1)+1)(k(J−1)+1)&x1&y1)^…^(a(k(I−1)+1)(k(J−1)+k)&x1&yk)^…^(a(k(I−1)+k)(k(J−1)+1)&xk&y1)^…^(a(k(I−1)+k)(k(J−1)+k)&xk&yk)が格納されている。
【0248】
(例3’)の場合、MビットのXOR演算(^)を(N/k)2回実行するだけで済む。但し、(例2’)のアルゴリズムに比べると、必要なメモリ量は、22k/k2倍となる。
【0249】
例えば、k=1のとき、MビットXOR演算が1202=14400回、必要なメモリ量が(例2’)の22=4倍、ループ回数は変化なしとなる。また、k=2のとき、MビットXOR演算が602=3600回、必要なメモリ量が24/4=4倍、ループ回数が1/4となる。k=4のとき、MビットXOR演算が302=900回、必要なメモリ量が28/42=16倍、ループ回数が1/16となる。k=6のとき、MビットXOR演算が202=400回、必要なメモリ量が212/62=114倍、ループ回数が1/36となる。k=8のとき、MビットXOR演算が152=225回、必要なメモリが216/82=1024倍、ループ回数が1/64となる。
【0250】
(例3’)
input x,y;
for I=1 to N/k
for J=I to N/k
[zの1〜Mビット目]^=a(1〜M)IJ[xのk(I−1)+1〜kビット目][yのk(J−1)+1〜kビット目];
end for
end for
output z;
【0251】
なお、(例3’)に示した手法は、ちょうど、下記の式(34)で定義されるGIJ(…)の値を予め計算し、配列として保持しておく手法と言える。
【0252】
【数20】

【0253】
以上、多変数多項式Gを計算するケースを例に挙げ、構造化手法#1に係る具体的なアルゴリズムの構成について説明した。かかる構成により、アルゴリズムを実行する際に処理の高速化が期待できる。
【0254】
(3次多変数多項式Fへの適用)
ここまで、構造化手法#1の具体例として、2次の多変数多項式の係数を構造化する手法を紹介してきたが、同様にして3次の多変数多項式の係数を構造化することも可能である。図24の例では、係数a1IJL〜aMIJLがデータ構造Aとして纏められ、係数b1IJ〜bMIJがデータ構造Bとして纏められ、係数c1I〜cMIがデータ構造Cとして纏められる。このように係数を構造化することで多変数多項式の計算が効率化される。
【0255】
例えば、データ構造Aに係る計算について具体的に考えてみたい。係数を構造化しない場合、当該データ構造Aに係る計算のアルゴリズムは、例えば、下記(例4)のようになる。
【0256】
(例4)
input x;
for Q=I to M
for I=1 to N
for J=I to N
for L=J to N
[yのQビット目]^=[aQIJL]&[xのIビット目]&[xのJビット目]&[xのLビット目];
end for
end for
end for
end for
output y;
【0257】
一方、係数を構造化すると、下記(例5)のようなアルゴリズムとなる。(例5)の場合、MビットのAND演算(&)を2×N×(N+1)×(N+2)/6回、MビットのXOR演算(^)を1×N×(N+1)×(N+2)/6回実行するだけで済む。なお、a(1〜M)IJLは、それぞれループのタイミングで生成される。また、係数を使い回してもよい。例えば、ループを実行する際、[a(1〜M)IJL]を毎回生成せず、M回に1回だけ生成するようにしてもよい。また、M回のループ中、[a(1〜M)IJ]を1ビットずつローテーションしながら利用してもよい。
【0258】
(例5)
input x;
for I=1 to N
for J=I to N
for L=J to N
[yの1〜Mビット目]^=[a(1〜M)IJL]&[xのIビット目]&[xのJビット目]&[xのLビット目];
end for
end for
output y;
【0259】
また、係数を構造化する場合、多変数多項式Fの係数を適用した中間の結果をテーブルに保持するようにしてもよい。この場合、上記のアルゴリズムは(例6)のようになる。なお、配列aIJL[0][0][0]〜aIJL[2k−1][2k−1][2k−1]には、それぞれ、aIJL[x1,…,xk][z1,…,zk][w1,…,wk]=Σ1≦α,β,γ≦k(a(k(I−1)+α)(k(J−1)+β)(k(L−1)+γ)&xα&zβ&wγ)が格納されている。(例6)の場合、MビットのXOR演算(^)を(N/k)(N/k+1)(N/k+2)/6回実行するだけで済む。但し、(例4)のアルゴリズムに比べると、必要なメモリ量は、23k/k3倍となる。
【0260】
例えば、k=1のとき、MビットXOR演算が120*121*122/6=295240回、必要なメモリ量が(例4)の23=8倍、ループ回数は変化なしとなる。また、k=2のとき、MビットXOR演算が60*61*62/6=37820回、必要なメモリ量が26/8=8倍、ループ回数が1/7.8となる。k=4のとき、MビットXOR演算が30*31*32/6=4960回、必要なメモリ量が212/43=64倍、ループ回数が1/59.5となる。k=6のとき、MビットXOR演算が20*21*22/6=1540回、必要なメモリ量が218/63=1214倍、ループ回数が1/192となる。
【0261】
(例6)
input x;
for I=1 to N/k
for J=I to N/k
for L=J to N/k
[yの1〜Mビット目]^=a(1〜M)IJL[xのk(I−1)+1〜kビット目][xのk(J−1)+1〜kビット目][xのk(L−1)+1〜kビット目];
end for
end for
end for
output y;
【0262】
なお、(例6)に示した手法は、ちょうど、下記の式(35)で定義されるFIJ(…)の値を予め計算し、配列として保持しておく手法と言える。
【0263】
【数21】

【0264】
以上、構造化手法#1を3次の多変数多項式Fへ適用するケースについて説明した。かかる構成により、アルゴリズムを実行する際に処理の高速化が期待できる。
【0265】
(3次多変数多項式Gx,Gyへの適用)
上記の(例5)や(例6)と同様、図25及び図26に示すように、3次の多変数多項式Gx,Gyに対しても構造化手法#1を適用することが可能である。構造化手法#1を適用しない場合、3次の多変数多項式Gxのデータ構造Aに係る計算は、例えば、下記の(例4’X)のアルゴリズムにより実行される。
【0266】
(例4’X)
input x,y;
for Q=1 to M
for I=1 to N
for J=1 to N
for L=1 to N
[zのQビット目]^=[aQIJL+aQILJ+aQLJI]&[yのIビット目]&[yのJビット目]&[xのLビット目];
end for
end for
end for
end for
output z;
【0267】
上記の(例4’X)に対し、上述した構造化手法#1を適用すると、多変数多項式Gxを計算するアルゴリズムは、下記の(例5’X)のようになる。また、上記の(例6)と同様にして多変数多項式Gxの係数を適用した中間の結果をテーブルに保持するようにしてもよい。
【0268】
(例5’X)
input x,y;
for I=1 to N
for J=1 to N
for L=1 to N
[zの1〜Mビット目]^=[a(1〜M)IJL+a(1〜M)ILJ+a(1〜M)LJI]&[yのIビット目]&[yのJビット目]&[xのLビット目];
end for
end for
end for
output z;
【0269】
また、構造化手法#1を適用しない場合、3次の多変数多項式Gyの計算は、例えば、下記の(例4’Y)のアルゴリズムにより実行される。
【0270】
(例4’Y)
input x,y;
for Q=1 to M
for I=1 to N
for J=1 to N
for L=1 to N
[zのQビット目]^=[aQIJL+aQILJ+aQLJI]&[xのIビット目]&[xのJビット目]&[yのLビット目];
end for
end for
end for
end for
output z;
【0271】
上記の(例4’Y)に対し、上述した構造化手法#1を適用すると、多変数多項式Gyを計算するアルゴリズムは、下記の(例5’Y)のようになる。また、上記の(例6)と同様にして多変数多項式Gyの係数を適用した中間の結果をテーブルに保持するようにしてもよい。
【0272】
(例5’Y)
input x,y;
for I=1 to N
for J=1 to N
for L=1 to N
[zの1〜Mビット目]^=[a(1〜M)IJL+a(1〜M)ILJ+a(1〜M)LJI]&[xのIビット目]&[xのJビット目]&[yのLビット目];
end for
end for
end for
output z;
【0273】
以上、構造化手法#1を3次の多変数多項式Gx、Gyへ適用するケースについて説明した。かかる構成により、アルゴリズムを実行する際に処理の高速化が期待できる。
【0274】
(7−2−2:構造化手法#2(図27))
次に、構造化手法#2について説明する。構造化手法#2は、図27に示すように、多変数多項式を2次形式で表現し、2次形式の行又は列を1つのデータ構造として纏める手法である。図27の例では、行方向にデータ構造が纏められている。
【0275】
図27に示すように係数を構造化し、生成した乱数を多変数多項式の係数として一部ずつ逐次適用していく場合、係数の代入アルゴリズムは(例4)のようになる。例4の場合、NビットのAND演算(&)を(N+1)×M回、NビットのXOR演算(^)をN×M回、関数Qの演算をM回実行するだけで済む。
【0276】
(例4)
for I=1 to N
T^=AI&[xのIビット目];
end for
T&=x;
output Q(T);
【0277】
Q(z){
z=z^(z>>1);
z=z^(z>>2);
z=z^(z>>4);
z=z^(z>>8);
・・・
z=z^(z>>2Log(N));
return z&1;
}
【0278】
また、図27に示すように係数を構造化し、多変数多項式の係数を適用した中間の結果をテーブルに保持するようにしてもよい。この場合、係数の代入アルゴリズムは(例5)のようになる。なお、配列AI[0]〜AI[2k−1]には、それぞれ、AI[x1,…,xk]=(A(k(I−1)+1)&x1)^…^(A(k(I−1)+k)&xk)が格納されている。例5の場合、NビットのXOR演算(^)を(N/k)×M、Nビットの関数Qの演算をM回実行するだけで済む。但し、(例4)のアルゴリズムに比べると、必要なメモリ量は、2k/k倍となる。
【0279】
例えば、k=1のとき、NビットXOR演算が120回、必要なメモリ量が(例4)の2倍、ループ回数は変化なしとなる。また、k=4のとき、NビットXOR演算が30回、必要なメモリ量が24/4=4倍、ループ回数が1/4となる。k=8のとき、NビットXOR演算が15回、必要なメモリが28/8=32倍、ループ回数が1/8となる。k=16のとき、NビットXOR演算が8回、必要なメモリが216/16=4096倍、ループ回数が1/15となる。
【0280】
(例5)
for I=1 to N/k
T^=AI[xのk(I−1)+1〜k(I−1)+kビット目];
end for
T&=x;
output Q(T);
【0281】
以上、構造化手法#2に係る具体的な係数の代入アルゴリズムについて説明した。かかる構成により、アルゴリズムを実行する際に処理の高速化が期待できる。
【0282】
(7−2−3:構造化手法#3)
次に、構造化手法#3について説明する。構造化手法#3は、同じ多変数多項式にN回(N≧2)代入処理を行なう場合に、乱数から多項式をN回生成して代入処理を行うのではなく、「係数を一部生成し、その部分に関するN回分の処理を行なう」部分を単位とする逐次的な処理をN回分並列して行なうという手法である。この手法を適用すると、乱数生成のコストが無視できない場合にN回分の処理全体でのスループットが改善される。
【0283】
例えば、図5に示したアルゴリズムでは、工程#1において引数を更新しながら多変数多項式F及びGの計算をN回繰り返し実行している。そこで、このような計算部分について、同じ係数を利用して繰り返し演算を行うように構成する。上記(例2)のアルゴリズムを用いて多変数多項式F(r0i)(i=1〜N)を計算する場合、一度生成した[aIJL]について、N個のr0iを全て適用した後で、次の[aIJL]に関する処理を実行するように構成する。このように構成すると、同じ係数[aIJL]をN回生成せずに済むようになる。
【0284】
以上、構造化手法#3に係る具体的な係数の代入アルゴリズムについて説明した。かかる構成により、N回分の処理におけるトータルでのスループットが改善される。
【0285】
<8:ハードウェア構成例(図28)>
上記の各アルゴリズムは、例えば、図28に示す情報処理装置のハードウェア構成を用いて実行することが可能である。つまり、当該各アルゴリズムの処理は、コンピュータプログラムを用いて図28に示すハードウェアを制御することにより実現される。なお、このハードウェアの形態は任意であり、例えば、パーソナルコンピュータ、携帯電話、PHS、PDA等の携帯情報端末、ゲーム機、接触式又は非接触式のICチップ、接触式又は非接触式のICカード、又は種々の情報家電がこれに含まれる。但し、上記のPHSは、Personal Handy−phone Systemの略である。また、上記のPDAは、Personal Digital Assistantの略である。
【0286】
図28に示すように、このハードウェアは、主に、CPU902と、ROM904と、RAM906と、ホストバス908と、ブリッジ910と、を有する。さらに、このハードウェアは、外部バス912と、インターフェース914と、入力部916と、出力部918と、記憶部920と、ドライブ922と、接続ポート924と、通信部926と、を有する。但し、上記のCPUは、Central Processing Unitの略である。また、上記のROMは、Read Only Memoryの略である。そして、上記のRAMは、Random Access Memoryの略である。
【0287】
CPU902は、例えば、演算処理装置又は制御装置として機能し、ROM904、RAM906、記憶部920、又はリムーバブル記録媒体928に記録された各種プログラムに基づいて各構成要素の動作全般又はその一部を制御する。ROM904は、CPU902に読み込まれるプログラムや演算に用いるデータ等を格納する手段である。RAM906には、例えば、CPU902に読み込まれるプログラムや、そのプログラムを実行する際に適宜変化する各種パラメータ等が一時的又は永続的に格納される。
【0288】
これらの構成要素は、例えば、高速なデータ伝送が可能なホストバス908を介して相互に接続される。一方、ホストバス908は、例えば、ブリッジ910を介して比較的データ伝送速度が低速な外部バス912に接続される。また、入力部916としては、例えば、マウス、キーボード、タッチパネル、ボタン、スイッチ、及びレバー等が用いられる。さらに、入力部916としては、赤外線やその他の電波を利用して制御信号を送信することが可能なリモートコントローラ(以下、リモコン)が用いられることもある。
【0289】
出力部918としては、例えば、CRT、LCD、PDP、又はELD等のディスプレイ装置、スピーカ、ヘッドホン等のオーディオ出力装置、プリンタ、携帯電話、又はファクシミリ等、取得した情報を利用者に対して視覚的又は聴覚的に通知することが可能な装置である。但し、上記のCRTは、Cathode Ray Tubeの略である。また、上記のLCDは、Liquid Crystal Displayの略である。そして、上記のPDPは、Plasma DisplayPanelの略である。さらに、上記のELDは、Electro−Luminescence Displayの略である。
【0290】
記憶部920は、各種のデータを格納するための装置である。記憶部920としては、例えば、ハードディスクドライブ(HDD)等の磁気記憶デバイス、半導体記憶デバイス、光記憶デバイス、又は光磁気記憶デバイス等が用いられる。但し、上記のHDDは、Hard Disk Driveの略である。
【0291】
ドライブ922は、例えば、磁気ディスク、光ディスク、光磁気ディスク、又は半導体メモリ等のリムーバブル記録媒体928に記録された情報を読み出し、又はリムーバブル記録媒体928に情報を書き込む装置である。リムーバブル記録媒体928は、例えば、DVDメディア、Blu−rayメディア、HD DVDメディア、各種の半導体記憶メディア等である。もちろん、リムーバブル記録媒体928は、例えば、非接触型ICチップを搭載したICカード、又は電子機器等であってもよい。但し、上記のICは、Integrated Circuitの略である。
【0292】
接続ポート924は、例えば、USBポート、IEEE1394ポート、SCSI、RS−232Cポート、又は光オーディオ端子等のような外部接続機器930を接続するためのポートである。外部接続機器930は、例えば、プリンタ、携帯音楽プレーヤ、デジタルカメラ、デジタルビデオカメラ、又はICレコーダ等である。但し、上記のUSBは、Universal Serial Busの略である。また、上記のSCSIは、Small Computer System Interfaceの略である。
【0293】
通信部926は、ネットワーク932に接続するための通信デバイスであり、例えば、有線又は無線LAN、Bluetooth(登録商標)、又はWUSB用の通信カード、光通信用のルータ、ADSL用のルータ、又は接触又は非接触通信用のデバイス等である。また、通信部926に接続されるネットワーク932は、有線又は無線により接続されたネットワークにより構成され、例えば、インターネット、家庭内LAN、赤外線通信、可視光通信、放送、又は衛星通信等である。但し、上記のLANは、Local Area Networkの略である。また、上記のWUSBは、Wireless USBの略である。そして、上記のADSLは、Asymmetric Digital Subscriber Lineの略である。
【0294】
<9:まとめ>
最後に、本技術の実施形態に係る技術内容について簡単に纏める。ここで述べる技術内容は、例えば、PC、携帯電話、ゲーム機、情報端末、情報家電、カーナビゲーションシステム等、種々の情報処理装置に対して適用することができる。なお、以下で述べる情報処理装置の機能は、1台の情報処理装置を利用して実現することも可能であるし、複数台の情報処理装置を利用して実現することも可能である。また、以下で述べる情報処理装置が処理を実行する際に用いるデータ記憶手段及び演算処理手段は、当該情報処理装置に設けられたものであってもよいし、ネットワークを介して接続された機器に設けられたものであってもよい。
【0295】
上記の情報処理装置の機能構成は以下のように表現される。例えば、下記(1)に記載の情報処理装置は、多次多変数連立方程式の求解困難性に安全性の根拠を置く効率的な公開鍵認証方式又は電子署名方式のアルゴリズムを実行する機能を有する。
【0296】
(1)
多次多変数多項式の組F=(f1,…,fm)を含む公開鍵を利用した公開鍵認証方式又は電子署名方式のアルゴリズムを実行するエンティティの間で共有されている情報から所定の関数を用いて、前記多次多変数多項式の組Fを構成する各項の係数に利用する数を生成する数生成部と、
前記数生成部が生成した数を、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式の係数に割り当てる割当部と、
を備え、
前記割当部は、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式の係数のうち、変数の組み合わせの種類が同じ項の係数をグループ化しておき、割り当て処理をグループ単位で実行する、
情報処理装置。
【0297】
(2)
多次多変数多項式の組F=(f1,…,fm)を含む公開鍵を利用した公開鍵認証方式又は電子署名方式のアルゴリズムを実行するエンティティの間で共有されている情報から所定の関数を用いて、前記多次多変数多項式の組Fを構成する各項の係数に利用する数を生成する数生成部と、
前記数生成部が生成した数を、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式の係数に割り当てる割当部と、
を備え、
前記割当部は、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式を2次形式で表現した場合の係数行列を行又は列毎にグループ化しておき、割り当て処理をグループ単位で実行する、
情報処理装置。
【0298】
(3)
前記数生成部は、前記割当部が1つのグループに対する割り当て処理を実行する際に、当該1つのグループに属する係数の分だけ前記数を生成する、
上記(1)又は(2)に記載の情報処理装置。
【0299】
(4)
前記数生成部は、前記1つのグループに属する係数の分だけ前記数を生成する際、1つの数を生成し、生成した数を1ビットずつローテーションして所要数の数を生成する、
上記(3)に記載の情報処理装置。
【0300】
(5)
前記各グループに対応する種類の項に前記係数を割り当て、当該項の変数に任意の数を代入した値をテーブルとして保持するテーブル保持部をさらに備える、
上記(1)又は(2)に記載の情報処理装置。
【0301】
(6)
多次多変数多項式の組F=(f1,…,fm)を含む公開鍵を利用した公開鍵認証方式又は電子署名方式のアルゴリズムを実行するエンティティの間で共有されている情報から所定の関数を用いて前記多次多変数多項式の組Fを構成する各項の係数と同じ数だけ数を生成する数生成部と、
前記証明者と前記認証者との間で予め決められた順序で前記数生成部が生成した数を、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式の係数に割り当てる割当部と、
を備える、
情報処理装置。
【0302】
(7)
前記情報は、乱数のシードであり、
前記所定の関数は、前記シードを利用して乱数を生成する乱数生成器である、
上記(1)〜(6)のいずれか1項に記載の情報処理装置。
【0303】
(8)
環K上で定義される多次多変数多項式の組F=(f1,…,fm)、及びベクトルs∈Knに基づいてメッセージを生成するメッセージ生成部と、
前記多次多変数多項式の組F及びベクトルy=(y1,…,ym)=(f1(s),…,fm(s))を保持する検証者に前記メッセージを提供するメッセージ提供部と、
k通り(k≧3)の検証パターンの中から前記検証者が選択した検証パターンに対応する回答情報を前記検証者に提供する回答提供部と、
を備え、
前記ベクトルsは秘密鍵であり、
前記多次多変数多項式の組F及び前記ベクトルyは公開鍵であり、
前記回答情報は、前記乱数の組及び前記メッセージの中から前記検証パターンに応じて選択される情報であり、
前記メッセージは、前記公開鍵及び前記回答情報を利用して、当該回答情報に対応する検証パターン用に予め用意された演算を実行することで得られる情報である、
上記(1)〜(7)のいずれか1項に記載の情報処理装置。
【0304】
(9)
環K上で定義される多次多変数多項式の組F=(f1,…,fm)及びベクトルy=(y1,…,ym)=(f1(s),…,fm(s))を保持する情報保持部と、
前記多次多変数多項式の組F及びベクトルs∈Knに基づいて生成されたメッセージを取得するメッセージ取得部と、
前記メッセージを提供した証明者に対し、k通り(k≧3)の検証パターンの中からランダムに選択した1つの検証パターンの情報を提供するパターン情報提供部と、
前記選択した検証パターンに対応する回答情報を前記証明者から取得する回答取得部と、
前記メッセージ、前記多次多変数多項式の組F、前記ベクトルy、及び前記回答情報に基づいて前記証明者が前記ベクトルsを保持しているか否かを検証する検証部と、
を備え、
前記ベクトルsは秘密鍵であり、
前記多次多変数多項式の組F及び前記ベクトルyは公開鍵であり、
前記メッセージは、前記公開鍵及び前記回答情報を利用して、当該回答情報に対応する検証パターン用に予め用意された演算を実行することで得られる情報である、
上記(1)〜(7)のいずれか1項に記載の情報処理装置。
【0305】
(10)
環K上で定義される多次多変数多項式の組F=(f1,…,fm)、及びベクトルs∈Knに基づいてメッセージを生成するメッセージ生成部と、
前記多次多変数多項式の組F及びベクトルy=(y1,…,ym)=(f1(s),…,fm(s))を保持する検証者に前記メッセージを提供するメッセージ提供部と、
前記検証者がランダムに選択した第1の情報及び前記メッセージを生成する際に得られる第2の情報を用いて第3の情報を生成する中間情報生成部と、
前記検証者に前記第3の情報を提供する中間情報提供部と、
k通り(k≧2)の検証パターンの中から前記検証者が選択した検証パターンに対応する回答情報を前記検証者に提供する回答提供部と、
を備え、
前記ベクトルsは秘密鍵であり、
前記多次多変数多項式の組F及び前記ベクトルyは公開鍵であり、
前記回答情報は、前記メッセージの中から前記検証パターンに応じて選択される情報であり、
前記メッセージは、前記公開鍵、前記第1の情報、前記第3の情報、前記回答情報を利用して、当該回答情報に対応する検証パターン用に予め用意された演算を実行することで得られる情報である、
上記(1)〜(7)のいずれか1項に記載の情報処理装置。
【0306】
(11)
環K上で定義される多次多変数多項式の組F=(f1,…,fm)及びベクトルy=(y1,…,ym)=(f1(s),…,fm(s))を保持する情報保持部と、
前記多次多変数多項式の組F及びベクトルs∈Knに基づいて生成されたメッセージを取得するメッセージ取得部と、
前記メッセージを提供した証明者に対し、ランダムに選択した第1の情報を提供する情報提供部と、
前記第1の情報及び前記メッセージを生成する際に得られる第2の情報を用いて前記証明者が生成した第3の情報を取得する中間情報取得部と、
k通り(k≧3)の検証パターンの中からランダムに選択した1つの検証パターンの情報を前記証明者に提供するパターン情報提供部と、
前記選択した検証パターンに対応する回答情報を前記証明者から取得する回答取得部と、
前記メッセージ、前記第1の情報、前記第3の情報、前記多次多変数多項式の組F、及び前記回答情報に基づいて前記証明者が前記ベクトルsを保持しているか否かを検証する検証部と、
を備え、
前記ベクトルsは秘密鍵であり、
前記多次多変数多項式の組F及び前記ベクトルyは公開鍵であり、
前記メッセージは、前記公開鍵、前記第1の情報、前記第3の情報、前記回答情報を利用して当該回答情報に対応する検証パターン用に予め用意された演算を実行することで得られる情報である、
上記(1)〜(7)のいずれか1項に記載の情報処理装置。
【0307】
(12)
前記アルゴリズムが複数回繰り返し実行される場合において、前記数生成部は1回だけ前記数を生成し、前記割当部は1回だけ前記割り当て処理を実行し、
前記アルゴリズムは、前記割当部が割り当てた係数を繰り返し利用する、
上記(1)又は(2)に記載の情報処理装置。
【0308】
(13)
環K上で定義される多次多変数多項式の組F=(f1,…,fm)、及び署名鍵s∈Knを用いて文書Mに対する電子署名を生成する署名生成部と、
前記多次多変数多項式の組F及びベクトルy=(f1(s),…,fm(s))を保持する検証者へと前記電子署名を提供する署名提供部と、
を備える、
上記(1)〜(7)のいずれか1項に記載の情報処理装置。
【0309】
(14)
多次多変数多項式の組F=(f1,…,fm)を含む公開鍵を利用した公開鍵認証方式又は電子署名方式のアルゴリズムを実行するエンティティの間で共有されている情報から所定の関数を用いて、前記多次多変数多項式の組Fを構成する各項の係数に利用する数を生成するステップと、
生成した数を、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式の係数に割り当てるステップと、
を含み、
前記割り当てるステップでは、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式の係数のうち、変数の組み合わせの種類が同じ項の係数をグループ化しておき、割り当て処理をグループ単位で実行する、
情報処理方法。
【0310】
(15)
多次多変数多項式の組F=(f1,…,fm)を含む公開鍵を利用した公開鍵認証方式又は電子署名方式のアルゴリズムを実行するエンティティの間で共有されている情報から所定の関数を用いて、前記多次多変数多項式の組Fを構成する各項の係数に利用する数を生成するステップと、
生成した数を、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式の係数に割り当てるステップと、
を含み、
前記割り当てるステップでは、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式を2次形式で表現した場合の係数行列を行又は列毎にグループ化しておき、割り当て処理をグループ単位で実行する、
情報処理方法。
【0311】
(16)
多次多変数多項式の組F=(f1,…,fm)を含む公開鍵を利用した公開鍵認証方式又は電子署名方式のアルゴリズムを実行するエンティティの間で共有されている情報から所定の関数を用いて前記多次多変数多項式の組Fを構成する各項の係数と同じ数だけ数を生成するステップと、
前記証明者と前記認証者との間で予め決められた順序で前記数生成部が生成した数を、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式の係数に割り当てるステップと、
を含む、
情報処理方法。
【0312】
(17)
多次多変数多項式の組F=(f1,…,fm)を含む公開鍵を利用した公開鍵認証方式又は電子署名方式のアルゴリズムを実行するエンティティの間で共有されている情報から所定の関数を用いて、前記多次多変数多項式の組Fを構成する各項の係数に利用する数を生成する数生成機能と、
前記数生成機能が生成した数を、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式の係数に割り当てる割当機能と、
をコンピュータに実現させるためのプログラムであり、
前記割当機能は、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式の係数のうち、変数の組み合わせの種類が同じ項の係数をグループ化しておき、割り当て処理をグループ単位で実行する、
プログラム。
【0313】
(18)
多次多変数多項式の組F=(f1,…,fm)を含む公開鍵を利用した公開鍵認証方式又は電子署名方式のアルゴリズムを実行するエンティティの間で共有されている情報から所定の関数を用いて、前記多次多変数多項式の組Fを構成する各項の係数に利用する数を生成する数生成機能と、
前記数生成機能が生成した数を、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式の係数に割り当てる割当機能と、
をコンピュータに実現させるためのプログラムであり、
前記割当機能は、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式を2次形式で表現した場合の係数行列を行又は列毎にグループ化しておき、割り当て処理をグループ単位で実行する、
プログラム。
【0314】
(19)
多次多変数多項式の組F=(f1,…,fm)を含む公開鍵を利用した公開鍵認証方式又は電子署名方式のアルゴリズムを実行するエンティティの間で共有されている情報から所定の関数を用いて前記多次多変数多項式の組Fを構成する各項の係数と同じ数だけ数を生成する数生成機能と、
前記証明者と前記認証者との間で予め決められた順序で前記数生成部が生成した数を、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式の係数に割り当てる割当機能と、
をコンピュータに実現させるためのプログラム。
【0315】
(20)
上記の(19)に記載のプログラムが記録された、コンピュータにより読み取り可能な記録媒体。
【0316】
(備考)
上記の証明者アルゴリズムP、検証者アルゴリズムV、署名生成アルゴリズムSig、署名検証アルゴリズムVerは、数生成部、割当部、テーブル保持部の一例である。上記の証明者アルゴリズムPは、メッセージ生成部、メッセージ提供部、回答提供部、中間情報生成部、中間情報提供部の一例である。また、上記の検証者アルゴリズムVは、情報保持部、メッセージ取得部、パターン情報提供部、回答取得部、検証部、中間情報取得部の一例である。
【0317】
以上、添付図面を参照しながら本技術の好適な実施形態について説明したが、本技術は係る例に限定されないことは言うまでもない。当業者であれば、特許請求の範囲に記載された範疇内において、各種の変更例または修正例に想到し得ることは明らかであり、それらについても当然に本技術の技術的範囲に属するものと了解される。
【0318】
上記の説明において、ハッシュ関数Hを用いるアルゴリズムを紹介したが、ハッシュ関数Hの代わりにコミットメント関数COMを用いてもよい。コミットメント関数COMは、文字列S及び乱数ρを引数にとる関数である。コミットメント関数の例としては、Shai HaleviとSilvio Micaliによって国際会議CRYPTO1996で発表された方式などがある。
【符号の説明】
【0319】
Gen 鍵生成アルゴリズム
P 証明者アルゴリズム
V 検証者アルゴリズム
Sig 署名生成アルゴリズム
Ver 署名検証アルゴリズム
【特許請求の範囲】
【請求項1】
多次多変数多項式の組F=(f1,…,fm)を含む公開鍵を利用した公開鍵認証方式又は電子署名方式のアルゴリズムを実行するエンティティの間で共有されている情報から所定の関数を用いて、前記多次多変数多項式の組Fを構成する各項の係数に利用する数を生成する数生成部と、
前記数生成部が生成した数を、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式の係数に割り当てる割当部と、
を備え、
前記割当部は、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式の係数のうち、変数の組み合わせの種類が同じ項の係数をグループ化しておき、割り当て処理をグループ単位で実行する、
情報処理装置。
【請求項2】
多次多変数多項式の組F=(f1,…,fm)を含む公開鍵を利用した公開鍵認証方式又は電子署名方式のアルゴリズムを実行するエンティティの間で共有されている情報から所定の関数を用いて、前記多次多変数多項式の組Fを構成する各項の係数に利用する数を生成する数生成部と、
前記数生成部が生成した数を、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式の係数に割り当てる割当部と、
を備え、
前記割当部は、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式を2次形式で表現した場合の係数行列を行又は列毎にグループ化しておき、割り当て処理をグループ単位で実行する、
情報処理装置。
【請求項3】
前記数生成部は、前記割当部が1つのグループに対する割り当て処理を実行する際に、当該1つのグループに属する係数の分だけ前記数を生成する、
請求項1に記載の情報処理装置。
【請求項4】
前記数生成部は、前記1つのグループに属する係数の分だけ前記数を生成する際、1つの数を生成し、生成した数を1ビットずつローテーションして所要数の数を生成する、
請求項3に記載の情報処理装置。
【請求項5】
前記各グループに対応する種類の項に前記係数を割り当て、当該項の変数に任意の数を代入した値をテーブルとして保持するテーブル保持部をさらに備える、
請求項1に記載の情報処理装置。
【請求項6】
多次多変数多項式の組F=(f1,…,fm)を含む公開鍵を利用した公開鍵認証方式又は電子署名方式のアルゴリズムを実行するエンティティの間で共有されている情報から所定の関数を用いて前記多次多変数多項式の組Fを構成する各項の係数と同じ数だけ数を生成する数生成部と、
前記証明者と前記認証者との間で予め決められた順序で前記数生成部が生成した数を、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式の係数に割り当てる割当部と、
を備える、
情報処理装置。
【請求項7】
前記情報は、乱数のシードであり、
前記所定の関数は、前記シードを利用して乱数を生成する乱数生成器である、
請求項1に記載の情報処理装置。
【請求項8】
環K上で定義される多次多変数多項式の組F=(f1,…,fm)、及びベクトルs∈Knに基づいてメッセージを生成するメッセージ生成部と、
前記多次多変数多項式の組F及びベクトルy=(y1,…,ym)=(f1(s),…,fm(s))を保持する検証者に前記メッセージを提供するメッセージ提供部と、
k通り(k≧3)の検証パターンの中から前記検証者が選択した検証パターンに対応する回答情報を前記検証者に提供する回答提供部と、
を備え、
前記ベクトルsは秘密鍵であり、
前記多次多変数多項式の組F及び前記ベクトルyは公開鍵であり、
前記回答情報は、前記乱数の組及び前記メッセージの中から前記検証パターンに応じて選択される情報であり、
前記メッセージは、前記公開鍵及び前記回答情報を利用して、当該回答情報に対応する検証パターン用に予め用意された演算を実行することで得られる情報である、
請求項1に記載の情報処理装置。
【請求項9】
環K上で定義される多次多変数多項式の組F=(f1,…,fm)及びベクトルy=(y1,…,ym)=(f1(s),…,fm(s))を保持する情報保持部と、
前記多次多変数多項式の組F及びベクトルs∈Knに基づいて生成されたメッセージを取得するメッセージ取得部と、
前記メッセージを提供した証明者に対し、k通り(k≧3)の検証パターンの中からランダムに選択した1つの検証パターンの情報を提供するパターン情報提供部と、
前記選択した検証パターンに対応する回答情報を前記証明者から取得する回答取得部と、
前記メッセージ、前記多次多変数多項式の組F、前記ベクトルy、及び前記回答情報に基づいて前記証明者が前記ベクトルsを保持しているか否かを検証する検証部と、
を備え、
前記ベクトルsは秘密鍵であり、
前記多次多変数多項式の組F及び前記ベクトルyは公開鍵であり、
前記メッセージは、前記公開鍵及び前記回答情報を利用して、当該回答情報に対応する検証パターン用に予め用意された演算を実行することで得られる情報である、
請求項1に記載の情報処理装置。
【請求項10】
環K上で定義される多次多変数多項式の組F=(f1,…,fm)、及びベクトルs∈Knに基づいてメッセージを生成するメッセージ生成部と、
前記多次多変数多項式の組F及びベクトルy=(y1,…,ym)=(f1(s),…,fm(s))を保持する検証者に前記メッセージを提供するメッセージ提供部と、
前記検証者がランダムに選択した第1の情報及び前記メッセージを生成する際に得られる第2の情報を用いて第3の情報を生成する中間情報生成部と、
前記検証者に前記第3の情報を提供する中間情報提供部と、
k通り(k≧2)の検証パターンの中から前記検証者が選択した検証パターンに対応する回答情報を前記検証者に提供する回答提供部と、
を備え、
前記ベクトルsは秘密鍵であり、
前記多次多変数多項式の組F及び前記ベクトルyは公開鍵であり、
前記回答情報は、前記メッセージの中から前記検証パターンに応じて選択される情報であり、
前記メッセージは、前記公開鍵、前記第1の情報、前記第3の情報、前記回答情報を利用して、当該回答情報に対応する検証パターン用に予め用意された演算を実行することで得られる情報である、
請求項1に記載の情報処理装置。
【請求項11】
環K上で定義される多次多変数多項式の組F=(f1,…,fm)及びベクトルy=(y1,…,ym)=(f1(s),…,fm(s))を保持する情報保持部と、
前記多次多変数多項式の組F及びベクトルs∈Knに基づいて生成されたメッセージを取得するメッセージ取得部と、
前記メッセージを提供した証明者に対し、ランダムに選択した第1の情報を提供する情報提供部と、
前記第1の情報及び前記メッセージを生成する際に得られる第2の情報を用いて前記証明者が生成した第3の情報を取得する中間情報取得部と、
k通り(k≧3)の検証パターンの中からランダムに選択した1つの検証パターンの情報を前記証明者に提供するパターン情報提供部と、
前記選択した検証パターンに対応する回答情報を前記証明者から取得する回答取得部と、
前記メッセージ、前記第1の情報、前記第3の情報、前記多次多変数多項式の組F、及び前記回答情報に基づいて前記証明者が前記ベクトルsを保持しているか否かを検証する検証部と、
を備え、
前記ベクトルsは秘密鍵であり、
前記多次多変数多項式の組F及び前記ベクトルyは公開鍵であり、
前記メッセージは、前記公開鍵、前記第1の情報、前記第3の情報、前記回答情報を利用して当該回答情報に対応する検証パターン用に予め用意された演算を実行することで得られる情報である、
請求項1に記載の情報処理装置。
【請求項12】
前記アルゴリズムが複数回繰り返し実行される場合において、前記数生成部は1回だけ前記数を生成し、前記割当部は1回だけ前記割り当て処理を実行し、
前記アルゴリズムは、前記割当部が割り当てた係数を繰り返し利用する、
請求項1に記載の情報処理装置。
【請求項13】
環K上で定義される多次多変数多項式の組F=(f1,…,fm)、及び署名鍵s∈Knを用いて文書Mに対する電子署名を生成する署名生成部と、
前記多次多変数多項式の組F及びベクトルy=(f1(s),…,fm(s))を保持する検証者へと前記電子署名を提供する署名提供部と、
を備える、
請求項1に記載の情報処理装置。
【請求項14】
多次多変数多項式の組F=(f1,…,fm)を含む公開鍵を利用した公開鍵認証方式又は電子署名方式のアルゴリズムを実行するエンティティの間で共有されている情報から所定の関数を用いて、前記多次多変数多項式の組Fを構成する各項の係数に利用する数を生成するステップと、
生成した数を、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式の係数に割り当てるステップと、
を含み、
前記割り当てるステップでは、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式の係数のうち、変数の組み合わせの種類が同じ項の係数をグループ化しておき、割り当て処理をグループ単位で実行する、
情報処理方法。
【請求項15】
多次多変数多項式の組F=(f1,…,fm)を含む公開鍵を利用した公開鍵認証方式又は電子署名方式のアルゴリズムを実行するエンティティの間で共有されている情報から所定の関数を用いて、前記多次多変数多項式の組Fを構成する各項の係数に利用する数を生成するステップと、
生成した数を、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式の係数に割り当てるステップと、
を含み、
前記割り当てるステップでは、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式を2次形式で表現した場合の係数行列を行又は列毎にグループ化しておき、割り当て処理をグループ単位で実行する、
情報処理方法。
【請求項16】
多次多変数多項式の組F=(f1,…,fm)を含む公開鍵を利用した公開鍵認証方式又は電子署名方式のアルゴリズムを実行するエンティティの間で共有されている情報から所定の関数を用いて前記多次多変数多項式の組Fを構成する各項の係数と同じ数だけ数を生成するステップと、
前記証明者と前記認証者との間で予め決められた順序で前記数生成部が生成した数を、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式の係数に割り当てるステップと、
を含む、
情報処理方法。
【請求項17】
多次多変数多項式の組F=(f1,…,fm)を含む公開鍵を利用した公開鍵認証方式又は電子署名方式のアルゴリズムを実行するエンティティの間で共有されている情報から所定の関数を用いて、前記多次多変数多項式の組Fを構成する各項の係数に利用する数を生成する数生成機能と、
前記数生成機能が生成した数を、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式の係数に割り当てる割当機能と、
をコンピュータに実現させるためのプログラムであり、
前記割当機能は、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式の係数のうち、変数の組み合わせの種類が同じ項の係数をグループ化しておき、割り当て処理をグループ単位で実行する、
プログラム。
【請求項18】
多次多変数多項式の組F=(f1,…,fm)を含む公開鍵を利用した公開鍵認証方式又は電子署名方式のアルゴリズムを実行するエンティティの間で共有されている情報から所定の関数を用いて、前記多次多変数多項式の組Fを構成する各項の係数に利用する数を生成する数生成機能と、
前記数生成機能が生成した数を、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式の係数に割り当てる割当機能と、
をコンピュータに実現させるためのプログラムであり、
前記割当機能は、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式を2次形式で表現した場合の係数行列を行又は列毎にグループ化しておき、割り当て処理をグループ単位で実行する、
プログラム。
【請求項19】
多次多変数多項式の組F=(f1,…,fm)を含む公開鍵を利用した公開鍵認証方式又は電子署名方式のアルゴリズムを実行するエンティティの間で共有されている情報から所定の関数を用いて前記多次多変数多項式の組Fを構成する各項の係数と同じ数だけ数を生成する数生成機能と、
前記証明者と前記認証者との間で予め決められた順序で前記数生成部が生成した数を、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式の係数に割り当てる割当機能と、
をコンピュータに実現させるためのプログラム。
【請求項1】
多次多変数多項式の組F=(f1,…,fm)を含む公開鍵を利用した公開鍵認証方式又は電子署名方式のアルゴリズムを実行するエンティティの間で共有されている情報から所定の関数を用いて、前記多次多変数多項式の組Fを構成する各項の係数に利用する数を生成する数生成部と、
前記数生成部が生成した数を、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式の係数に割り当てる割当部と、
を備え、
前記割当部は、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式の係数のうち、変数の組み合わせの種類が同じ項の係数をグループ化しておき、割り当て処理をグループ単位で実行する、
情報処理装置。
【請求項2】
多次多変数多項式の組F=(f1,…,fm)を含む公開鍵を利用した公開鍵認証方式又は電子署名方式のアルゴリズムを実行するエンティティの間で共有されている情報から所定の関数を用いて、前記多次多変数多項式の組Fを構成する各項の係数に利用する数を生成する数生成部と、
前記数生成部が生成した数を、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式の係数に割り当てる割当部と、
を備え、
前記割当部は、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式を2次形式で表現した場合の係数行列を行又は列毎にグループ化しておき、割り当て処理をグループ単位で実行する、
情報処理装置。
【請求項3】
前記数生成部は、前記割当部が1つのグループに対する割り当て処理を実行する際に、当該1つのグループに属する係数の分だけ前記数を生成する、
請求項1に記載の情報処理装置。
【請求項4】
前記数生成部は、前記1つのグループに属する係数の分だけ前記数を生成する際、1つの数を生成し、生成した数を1ビットずつローテーションして所要数の数を生成する、
請求項3に記載の情報処理装置。
【請求項5】
前記各グループに対応する種類の項に前記係数を割り当て、当該項の変数に任意の数を代入した値をテーブルとして保持するテーブル保持部をさらに備える、
請求項1に記載の情報処理装置。
【請求項6】
多次多変数多項式の組F=(f1,…,fm)を含む公開鍵を利用した公開鍵認証方式又は電子署名方式のアルゴリズムを実行するエンティティの間で共有されている情報から所定の関数を用いて前記多次多変数多項式の組Fを構成する各項の係数と同じ数だけ数を生成する数生成部と、
前記証明者と前記認証者との間で予め決められた順序で前記数生成部が生成した数を、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式の係数に割り当てる割当部と、
を備える、
情報処理装置。
【請求項7】
前記情報は、乱数のシードであり、
前記所定の関数は、前記シードを利用して乱数を生成する乱数生成器である、
請求項1に記載の情報処理装置。
【請求項8】
環K上で定義される多次多変数多項式の組F=(f1,…,fm)、及びベクトルs∈Knに基づいてメッセージを生成するメッセージ生成部と、
前記多次多変数多項式の組F及びベクトルy=(y1,…,ym)=(f1(s),…,fm(s))を保持する検証者に前記メッセージを提供するメッセージ提供部と、
k通り(k≧3)の検証パターンの中から前記検証者が選択した検証パターンに対応する回答情報を前記検証者に提供する回答提供部と、
を備え、
前記ベクトルsは秘密鍵であり、
前記多次多変数多項式の組F及び前記ベクトルyは公開鍵であり、
前記回答情報は、前記乱数の組及び前記メッセージの中から前記検証パターンに応じて選択される情報であり、
前記メッセージは、前記公開鍵及び前記回答情報を利用して、当該回答情報に対応する検証パターン用に予め用意された演算を実行することで得られる情報である、
請求項1に記載の情報処理装置。
【請求項9】
環K上で定義される多次多変数多項式の組F=(f1,…,fm)及びベクトルy=(y1,…,ym)=(f1(s),…,fm(s))を保持する情報保持部と、
前記多次多変数多項式の組F及びベクトルs∈Knに基づいて生成されたメッセージを取得するメッセージ取得部と、
前記メッセージを提供した証明者に対し、k通り(k≧3)の検証パターンの中からランダムに選択した1つの検証パターンの情報を提供するパターン情報提供部と、
前記選択した検証パターンに対応する回答情報を前記証明者から取得する回答取得部と、
前記メッセージ、前記多次多変数多項式の組F、前記ベクトルy、及び前記回答情報に基づいて前記証明者が前記ベクトルsを保持しているか否かを検証する検証部と、
を備え、
前記ベクトルsは秘密鍵であり、
前記多次多変数多項式の組F及び前記ベクトルyは公開鍵であり、
前記メッセージは、前記公開鍵及び前記回答情報を利用して、当該回答情報に対応する検証パターン用に予め用意された演算を実行することで得られる情報である、
請求項1に記載の情報処理装置。
【請求項10】
環K上で定義される多次多変数多項式の組F=(f1,…,fm)、及びベクトルs∈Knに基づいてメッセージを生成するメッセージ生成部と、
前記多次多変数多項式の組F及びベクトルy=(y1,…,ym)=(f1(s),…,fm(s))を保持する検証者に前記メッセージを提供するメッセージ提供部と、
前記検証者がランダムに選択した第1の情報及び前記メッセージを生成する際に得られる第2の情報を用いて第3の情報を生成する中間情報生成部と、
前記検証者に前記第3の情報を提供する中間情報提供部と、
k通り(k≧2)の検証パターンの中から前記検証者が選択した検証パターンに対応する回答情報を前記検証者に提供する回答提供部と、
を備え、
前記ベクトルsは秘密鍵であり、
前記多次多変数多項式の組F及び前記ベクトルyは公開鍵であり、
前記回答情報は、前記メッセージの中から前記検証パターンに応じて選択される情報であり、
前記メッセージは、前記公開鍵、前記第1の情報、前記第3の情報、前記回答情報を利用して、当該回答情報に対応する検証パターン用に予め用意された演算を実行することで得られる情報である、
請求項1に記載の情報処理装置。
【請求項11】
環K上で定義される多次多変数多項式の組F=(f1,…,fm)及びベクトルy=(y1,…,ym)=(f1(s),…,fm(s))を保持する情報保持部と、
前記多次多変数多項式の組F及びベクトルs∈Knに基づいて生成されたメッセージを取得するメッセージ取得部と、
前記メッセージを提供した証明者に対し、ランダムに選択した第1の情報を提供する情報提供部と、
前記第1の情報及び前記メッセージを生成する際に得られる第2の情報を用いて前記証明者が生成した第3の情報を取得する中間情報取得部と、
k通り(k≧3)の検証パターンの中からランダムに選択した1つの検証パターンの情報を前記証明者に提供するパターン情報提供部と、
前記選択した検証パターンに対応する回答情報を前記証明者から取得する回答取得部と、
前記メッセージ、前記第1の情報、前記第3の情報、前記多次多変数多項式の組F、及び前記回答情報に基づいて前記証明者が前記ベクトルsを保持しているか否かを検証する検証部と、
を備え、
前記ベクトルsは秘密鍵であり、
前記多次多変数多項式の組F及び前記ベクトルyは公開鍵であり、
前記メッセージは、前記公開鍵、前記第1の情報、前記第3の情報、前記回答情報を利用して当該回答情報に対応する検証パターン用に予め用意された演算を実行することで得られる情報である、
請求項1に記載の情報処理装置。
【請求項12】
前記アルゴリズムが複数回繰り返し実行される場合において、前記数生成部は1回だけ前記数を生成し、前記割当部は1回だけ前記割り当て処理を実行し、
前記アルゴリズムは、前記割当部が割り当てた係数を繰り返し利用する、
請求項1に記載の情報処理装置。
【請求項13】
環K上で定義される多次多変数多項式の組F=(f1,…,fm)、及び署名鍵s∈Knを用いて文書Mに対する電子署名を生成する署名生成部と、
前記多次多変数多項式の組F及びベクトルy=(f1(s),…,fm(s))を保持する検証者へと前記電子署名を提供する署名提供部と、
を備える、
請求項1に記載の情報処理装置。
【請求項14】
多次多変数多項式の組F=(f1,…,fm)を含む公開鍵を利用した公開鍵認証方式又は電子署名方式のアルゴリズムを実行するエンティティの間で共有されている情報から所定の関数を用いて、前記多次多変数多項式の組Fを構成する各項の係数に利用する数を生成するステップと、
生成した数を、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式の係数に割り当てるステップと、
を含み、
前記割り当てるステップでは、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式の係数のうち、変数の組み合わせの種類が同じ項の係数をグループ化しておき、割り当て処理をグループ単位で実行する、
情報処理方法。
【請求項15】
多次多変数多項式の組F=(f1,…,fm)を含む公開鍵を利用した公開鍵認証方式又は電子署名方式のアルゴリズムを実行するエンティティの間で共有されている情報から所定の関数を用いて、前記多次多変数多項式の組Fを構成する各項の係数に利用する数を生成するステップと、
生成した数を、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式の係数に割り当てるステップと、
を含み、
前記割り当てるステップでは、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式を2次形式で表現した場合の係数行列を行又は列毎にグループ化しておき、割り当て処理をグループ単位で実行する、
情報処理方法。
【請求項16】
多次多変数多項式の組F=(f1,…,fm)を含む公開鍵を利用した公開鍵認証方式又は電子署名方式のアルゴリズムを実行するエンティティの間で共有されている情報から所定の関数を用いて前記多次多変数多項式の組Fを構成する各項の係数と同じ数だけ数を生成するステップと、
前記証明者と前記認証者との間で予め決められた順序で前記数生成部が生成した数を、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式の係数に割り当てるステップと、
を含む、
情報処理方法。
【請求項17】
多次多変数多項式の組F=(f1,…,fm)を含む公開鍵を利用した公開鍵認証方式又は電子署名方式のアルゴリズムを実行するエンティティの間で共有されている情報から所定の関数を用いて、前記多次多変数多項式の組Fを構成する各項の係数に利用する数を生成する数生成機能と、
前記数生成機能が生成した数を、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式の係数に割り当てる割当機能と、
をコンピュータに実現させるためのプログラムであり、
前記割当機能は、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式の係数のうち、変数の組み合わせの種類が同じ項の係数をグループ化しておき、割り当て処理をグループ単位で実行する、
プログラム。
【請求項18】
多次多変数多項式の組F=(f1,…,fm)を含む公開鍵を利用した公開鍵認証方式又は電子署名方式のアルゴリズムを実行するエンティティの間で共有されている情報から所定の関数を用いて、前記多次多変数多項式の組Fを構成する各項の係数に利用する数を生成する数生成機能と、
前記数生成機能が生成した数を、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式の係数に割り当てる割当機能と、
をコンピュータに実現させるためのプログラムであり、
前記割当機能は、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式を2次形式で表現した場合の係数行列を行又は列毎にグループ化しておき、割り当て処理をグループ単位で実行する、
プログラム。
【請求項19】
多次多変数多項式の組F=(f1,…,fm)を含む公開鍵を利用した公開鍵認証方式又は電子署名方式のアルゴリズムを実行するエンティティの間で共有されている情報から所定の関数を用いて前記多次多変数多項式の組Fを構成する各項の係数と同じ数だけ数を生成する数生成機能と、
前記証明者と前記認証者との間で予め決められた順序で前記数生成部が生成した数を、前記多次多変数多項式の組Fを構成要素に含む多次多変数多項式の係数に割り当てる割当機能と、
をコンピュータに実現させるためのプログラム。
【図1】


【図2】


【図3】


【図4】


【図5】


【図6】


【図7】


【図8】


【図9】


【図10】


【図11】


【図12】


【図13】


【図14】


【図15】


【図16】


【図17】


【図18】


【図19】


【図20】


【図21】


【図22】


【図23】


【図24】


【図25】


【図26】


【図27】


【図28】




【図2】


【図3】


【図4】


【図5】


【図6】


【図7】


【図8】


【図9】


【図10】


【図11】


【図12】


【図13】


【図14】


【図15】


【図16】


【図17】


【図18】


【図19】


【図20】


【図21】


【図22】


【図23】


【図24】


【図25】


【図26】


【図27】


【図28】


【公開番号】特開2013−66151(P2013−66151A)
【公開日】平成25年4月11日(2013.4.11)
【国際特許分類】
【出願番号】特願2012−46687(P2012−46687)
【出願日】平成24年3月2日(2012.3.2)
【出願人】(000002185)ソニー株式会社 (34,172)
【Fターム(参考)】
【公開日】平成25年4月11日(2013.4.11)
【国際特許分類】
【出願日】平成24年3月2日(2012.3.2)
【出願人】(000002185)ソニー株式会社 (34,172)
【Fターム(参考)】
[ Back to top ]

