数値計算方法、プログラムおよび記録媒体
【課題】保存形IDO法を含めたIDO法に適用することで計算精度を向上させることができる数値計算方法を提供すること。
【解決手段】本発明は、流体に関する数値計算を行う局所補間微分オペレータ法を実行する数値計算装置による数値計算方法である。数値計算装置は、記憶部と演算部を有し、記憶部は、時間積分を行う変数の値と、その変数に関する補間関数とを記憶する。そして、演算部は、偏微分方程式に関して、時間軸上の固定点以外の流動点による影響も考慮した方程式解法であるラグランジュ法を移流項に適用するセミラグランジュ移流を、前記補間関数を使って前記偏微分方程式の移流項に対して行うことで前記時間積分を行う。
【解決手段】本発明は、流体に関する数値計算を行う局所補間微分オペレータ法を実行する数値計算装置による数値計算方法である。数値計算装置は、記憶部と演算部を有し、記憶部は、時間積分を行う変数の値と、その変数に関する補間関数とを記憶する。そして、演算部は、偏微分方程式に関して、時間軸上の固定点以外の流動点による影響も考慮した方程式解法であるラグランジュ法を移流項に適用するセミラグランジュ移流を、前記補間関数を使って前記偏微分方程式の移流項に対して行うことで前記時間積分を行う。
【発明の詳細な説明】
【技術分野】
【0001】
本発明は、偏微分方程式の演算に使用する数値計算方法、プログラムおよび記録媒体に関する。
【背景技術】
【0002】
近年、流体(液体や気体など)、電磁波、熱などに関する数値計算(シミュレーション)についての研究や開発が活発になってきている。
そのような数値計算を行う場合、流体などの変数(速度、圧力、温度、密度など)に関する偏微分方程式を、離散化された空間および時間に関して解く、という手法が用いられるのが一般的である。なぜなら、偏微分方程式の数学的な解析解(厳密解)を求めることは現実的に不可能だからである。したがって、高精度の数値計算方法を開発することが重要となる。
【0003】
そして、より高精度な計算を行うため、変数の値だけでなく変数の微分係数(空間勾配)の値も従属変数とするマルチモーメント手法であるCIP法(Cubic-Interpolated Pseudo-Particle Scheme)やIDO法(Interpolated Differential Operator Scheme:局所補間微分オペレータ法)が開発された。
【0004】
IDO法は、物理的に保存しなければならない質量、運動量、エネルギーを厳密に保存する保存形IDO法と、高精度数値計算の範囲内で物理的な保存を満足する非保存形IDO法とに大別することができる。保存形IDO法は、たとえば、変数の区間積分値(以下、単に「積分値」という。)を従属変数とすることで、その変数に関する物理量を保存することができる。
【0005】
そして、一般的に、計算の精度は保存形IDO法のほうがよい。しかし、保存形IDO法は値や積分値の定義点が異なるためにプログラムが複雑になるのに対し、非保存形IDO法は値と微分値が同じ格子点上に定義されるため、プログラムの構造が簡単になり境界条件も取り扱い易くなる。つまり、保存形IDO法と非保存形IDO法は、それぞれ一長一短を有し、場面や状況に応じて選択および使用される。
【0006】
そして、本出願人は、特許文献1において、非保存形IDO法における変数間の安定化カップリングの技術について提案した。この技術によれば、非保存形IDO法における数値計算の精度を向上させることができる。
【特許文献1】特開2006−318355号公報
【発明の開示】
【発明が解決しようとする課題】
【0007】
しかしながら、特許文献1の技術は、非保存形IDO法に使用するものであり、保存形IDO法に使用することはできない。つまり、保存形IDO法の計算精度の向上には、特許文献1の技術とは別の技術が必要となる。
そこで、本発明は、前記問題点に鑑みてなされたものであり、保存形IDO法を含めたIDO法に適用することで計算精度を向上させることができる数値計算方法、プログラムおよび記録媒体を提供することを目的とする。
【課題を解決するための手段】
【0008】
前記課題を解決するために、本発明は、複数の定義点における1つ以上の変数とその微分係数を含んだ複数の値を用いて偏微分方程式に関する演算を行い、変数のうち少なくともいずれか1つの変数を時間積分することにより、流体に関する数値計算を行う局所補間微分オペレータ法を実行する数値計算装置による数値計算方法である。
数値計算装置は、記憶部と演算部を有し、記憶部は、時間積分を行う変数の値と、その変数に関する補間関数とを記憶する。
そして、演算部は、偏微分方程式に関して、時間軸上の固定点以外の流動点による影響も考慮した方程式解法であるラグランジュ法を移流項に適用するセミラグランジュ移流を、補間関数を使って偏微分方程式の移流項に対して行うことで時間積分を行う。
また、当該数値計算方法をコンピュータに実行させるためのプログラムを作成し、さらに、そのプログラムを記録媒体に記録することができる。
【発明の効果】
【0009】
本発明によれば、保存形IDO法を含めたIDO法において、計算精度を向上させることができる。
【発明を実施するための最良の形態】
【0010】
以下、本発明の各実施形態について、適宜図面を参照しながら説明する。なお、本実施形態において、方程式の解法のうち、時間軸上の固定点に基づく解法をオイラー法といい、時間軸上の固定点以外の流動点による影響も考慮した解法をラグランジュ法という。また、偏微分方程式において、移流項にラグランジュ法を適用し、非移流項にオイラー法を適用する解法のことをセミラグランジュ(「セミラグ」と略記することもある。)法という。さらに、移流項に対してラグランジュ法を適用することを、「セミラグランジュ移流する(を行う)」と呼ぶ。ここで、移流項とは、ある物理量の局所変化を考える際に、対象物(流体など)自体の移動速度ベクトルとその物理量(またはその物理量の空間勾配)の空間勾配の内積に負の符号をつけた項のことを指す。また、移流項以外の項を非移流項という。
【0011】
図1および図2は各実施形態の説明に共通であり、まず、図1を参照しながら、数値計算方法を行う数値計算装置の構成について説明する。図1は、数値計算装置の構成図である。
数値計算装置10は、入力部1、記憶部2、メモリ3、演算部4および出力部5を備えて構成されるコンピュータ装置であり、たとえば、パソコン、ワークステーション、スーパーコンピュータなどにより実現することができる。
なお、演算部4は、ここでは1つとしているが、複数設けることにより並列計算を行うようにしてもよい。
【0012】
入力部1は、数値計算装置10の使用者(以下、単に「使用者」という)が各種情報を入力する手段であり、たとえば、キーボード、マウスなどである。
記憶部2は、各種情報を記憶するものであり、たとえば、ROM(Read Only Memory)、ハードディスクなどである。記憶部2は、ここでは、流体の数値計算(シミュレーション)を行うために、数値計算を行う場所を示す定義点である格子点、物理量(変数)やその微分係数の初期条件、支配方程式(自然現象を表わす偏微分方程式など)、補間関数、各種プログラムなどを記憶している。
【0013】
メモリ3は、演算部4が使用する一時記憶手段であり、たとえば、RAM(Random Access Memory)などである。
演算部4は、記憶部2に記憶された各種情報(プログラム、データなど)などに基づいて演算(処理)を行うものであり、たとえば、CPU(Central Processing Unit)である。
出力部5は、演算部4による演算の結果を出力するものであり、たとえば、ディスプレイなどである。
【0014】
次に、図2を参照しながら、数値計算の演算について説明する(適宜図1参照)。図2は、流体の数値計算の演算の大まかな流れを表わしたフローチャートである。
【0015】
まず、使用者が入力部1によって数値計算の開始に関する操作を行うと、演算部4は、記憶部2に記憶された情報に基づいて、演算を行う場所を示す定義点である格子点、各物理量の初期条件などを設定する(ステップS1)。
格子点は、たとえば、1次元の場合は「128」、2次元の場合は「32×32」、3次元の場合は「16×16×8」、といったように設定される。また、各物理量の初期条件としては、それぞれの格子点における変数の値、および、それらの値の微分係数(空間勾配)などが設定される。変数としては、たとえば、流体の速度、圧力、温度、密度などが挙げられる。
【0016】
次に、演算部4は、記憶部2に記憶された情報に基づいて、時間と空間に関する偏微分方程式などからなる支配方程式、各物理量の値を修正するための補間関数などを設定する(ステップS2)。
支配方程式としては、たとえば、圧縮性流体の運動方程式、流体の質量保存方程式などが挙げられ、詳細については後記する。また、補間関数としては、2次関数、3次関数、分母に関数を有する有理関数などが挙げられ、詳細については後記する。
【0017】
続いて、演算部4は、ステップS1およびステップS2で設定した各種情報を用い、時刻「t」における各格子点での各物理量の値に基づいて、時刻「t+1」における各格子点での各物理量の値を算出する、という演算をt=0,1,2,・・・nに関して行う(ステップS3〜ステップS5)。
そして、このステップS4における演算が本発明のポイントであるが、その詳細については後記する。
【0018】
次に、演算部4は、ステップS3〜ステップS5で算出した各物理量の値を、出力部5に出力する(ステップS6)。以上で、数値計算が完了する。
【0019】
(第1実施形態)
続いて、本発明の第1実施形態について説明する。第1実施形態は、保存形IDO法を用いた数値計算の例である。第1実施形態について説明する前に、その理解を助けるため、図9、図10Aおよび図10Bを参照しながら、保存形IDO法を用いた数値計算の比較例(従来技術)について説明する。図9は、比較例の保存形IDO法における変数イメージを示した図である。図10Aおよび図10Bは、比較例の保存形IDO法におけるルンゲクッタ法による時間更新(時間積分)を示した図である。
【0020】
なお、第1実施形態において、移流項における微分値の算出には風上補間(2つの格子点のうち風下側(流れの下流側)の格子点を中心にして行う補間)を用い、非移流項における微分値の算出には中心補間(3つの格子点のうちの真ん中の格子点を中心にして行う補間)を用いる。
【0021】
比較例では、支配方程式として、拡散項を有する一次元質量保存の偏微分方程式である式(1)を使用する。なお、流体に関して、ρは密度、uは速度、tは時間、xは座標を表す変数である。また、κ(カッパ)は拡散係数(物質の拡散の度合を示す係数)であり、あらかじめ与えられる。なお、速度uを求めるための式が別に必要であるが、その記載を省略し、速度uはその式によってすでに求められているものとする。
【数1】

【0022】
そして、実際に数値計算を行うことができるように、式(1)を変形して式(2)とする。なお、式(2)において「i」が付与された各変数は、複数の格子点のうち「i」番目の格子点上の変数であることを意味する。また、∂ρ/∂x|iは補間関数を用いた風上補間から求められる値である(詳細は後記)。さらに、∂u/∂x|iおよび∂2ρ/∂x2|iは補間関数を用いた中心補間から求められる値である(詳細は後記)。なお、本実施形態において、右側に「|i」が付与された項は、「座標「i」における、補間関数を用いて算出される値」であることを意味する。
【数2】

【0023】
さらに、ρの積分値を式(3)と定義し、その積分値に関する方程式を式(4)と定義する。なお、式(3)において記載されている「i+1/2」は、積分区間の両端(「i」と「i+1」)の中間地点を表している。また、式(4)において、「i+1」が付与された各変数は「i+1」番目の格子点上の変数であることを意味する。
【数3】

【0024】
また、∂ρ/∂x|iの風上補間に用いられる補間関数を式(5)と定義する。式(6)〜(8)は、その拘束条件である。これらの式(5)〜(8)から、補間係数a,bおよびcが式(9)〜(11)のように求められる。また、式(12)に示したように、ρiを微分したρx,i(=∂ρ/∂x|i)はbと等しくなる。
【数4】

【0025】
このような条件の下で、図10Aおよび図10Bに示したように、ルンゲクッタ法による時間更新(時間積分)を行う。ここでの目的は、時刻「n」における密度(ρni)と各係数(k1,i〜k4,i)から時刻「n+1」における密度(ρn+1i)を求めること(式(1015)参照)と、時刻「n」における密度の積分値(ρ-X,ni+1/2)と各係数(m1,i+1/2〜m4,i+1/2)から時刻「n+1」における密度(ρ-X,n+1i+1/2)を求めること(式(1016)参照)である。式(1001)〜式(1014)は、各係数(k1,i〜k4,i,m1,i+1/2〜m4,i+1/2)を求めるための式である。
【0026】
まず、式(1001)と式(1002)によって、k1,i(以下、「k1」とも表記する。k2,i〜k4,iについても同様)とm1,i+1/2(以下、「m1」とも表記する。m2,i+1/2〜m4,i+1/2についても同様)を求める。ここで、ui,ui+1,ρi,ρi+1の値は、時刻「n」における値としてすでに求められているものを使用することができる。なお、移流項である「−ui∂ρ/∂x|i」における「∂ρ/∂x|i」は、前記したように風上補間によって求めることができる。
【0027】
また、∂u/∂x|iはuの補間関数から求めることができる。ここでは、たとえば、uの補間関数として4次関数を使用し、中心補間によって∂u/∂x|iを求めることができる。その場合、3つの格子点の座標を「i-1」,「i」および「i+1」とし、補間関数をf(X)、その積分値(前記式(8)と同様)をfX(X)すると、その補間関数は、f(i-1),f(i),f(i+1),fX(i-1/2)およびfX(i+1/2)の拘束条件から決定することができる。∂2ρ/∂x2|iおよび非移流項中の∂ρ/∂x|iについても、同様にして中心補間から求めることができる。
【0028】
Δtは、時刻「n」と時刻「n+1」の差の時間長(時間刻み幅)である。なお、この式(1001)と式(1002)によって演算が行われる段階では、すべての格子点に関して演算が行われ、その後、次の演算に進む。以降についても同様である。
【0029】
次に、式(1003)と式(1004)によって、ρ*i(ρn+1iの暫定値)とρ-X,*i+1/2(ρ-X,n+1i+1/2の暫定値)を求める。ここで、ρi,ρ-Xi+1/2は、時刻「n」における値としてすでに求められているものを使用することができる。また、k1とm1は、それぞれ式(1001)と式(1002)で求められた値である。
【0030】
そして、式(1005)と式(1006)によって、k2,iとm2,i+1/2を求める。ここで、ρ*i(ρ*i+1も同様)は、式(1003)で求められた値である。また、移流項における∂ρ*/∂x|i(ρ*x,i)は、式(12)からbであることがわかり、前記した式(10)の右辺に、式(1003)と式(1004)から求められたρ*i,ρ*i-1,ρ-X,*i-1/2を代入することにより求められる。また、∂2ρ*/∂x2|iおよび非移流項中の∂ρ*/∂x|iについては、中心補間から求めることができる。
【0031】
以下、同様にして、式(1007)〜式(1014)を使うことにより、k1,i〜k4,i,m1,i+1/2〜m4,i+1/2の値をすべて求めることができる。そして、前記したように、式(1015)と式(1016)を使って、ρn+1iとρ-X,n+1i+1/2を求めることができる。なお、式(1007)と式(1011)においてρ*iは新たに更新され、式(1008)と式(1012)においてρ-X,*i+1/2は新たに更新される。
【0032】
次に、図3〜図6を参照しながら、本発明の第1実施形態の部分セミラグ保存形IDO法(セミラグランジュ法を部分的に適用した保存形IDO法)について説明する。
第1実施形態では、計算に、前記した比較例の場合と同じ式(1)〜式(11)を使用するので、重複説明を適宜省略する。なお、第1実施形態は、式(2)における右辺の移流項である第1項の「−ui∂ρ/∂x|i」に関してセミラグランジュ移流を行う点で、比較例における計算と異なっている。
【0033】
第1実施形態では、式(5)に対して、X=xi−uiΔtを代入することで、Δtの分だけセミラグランジュ移流したρの値であるρSLi,Δtを算出することができる(式(13)参照)。なお、式(13)において、Fni(X),anおよびbnは、時刻「n」におけるそれぞれの値であることを意味している。また、式(13)におけるΔtをΔt/2と置き換えることで、Δt/2の分だけセミラグランジュ移流したρの値であるρSLi,Δt/2を算出することができる。
【数5】

【0034】
ここで、図3は、第1実施形態の部分セミラグ保存形IDO法における変数イメージを示した図である。図3に示したように、このρSLi,Δtの値を用いて、時刻「n+1」における密度(ρn+1i)を求めることができる(詳細は後記)。
【0035】
次に、図4A〜図4Cを参照しながら、第1実施形態における数値計算装置の演算(処理)について説明する(適宜他図参照)。図4A〜図4Cは、第1実施形態における数値計算装置の演算を示したフローチャートである。数値計算装置10の演算部4は、記憶部2とメモリ3を使用しながら各演算を行う。そして、この演算の目的は、比較例の場合と同様、時刻「n」における密度(ρi)やその積分値(ρ-Xi+1/2(ρ-X,ni+1/2))などに基づいて、時刻「n+1」における密度(ρn+1i)と積分値(ρ-X,n+1i+1/2)を求めることである(ステップS410参照)。つまり、比較例の場合と同様、時刻「n」におけるρi,ρ-Xi+1/2,ui,ui+1,ρi,ρi+1などの値はすでに求められているものとして、以下の演算を行う。また、∂u/∂x|i,∂2ρ/∂x2|i,∂ρ/∂x|iなどは、前記した比較例の場合と同様、中心補間によって求められる。
【0036】
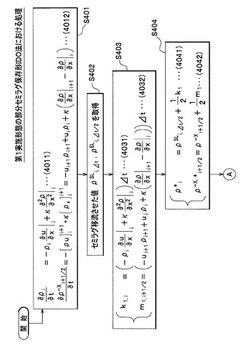
演算部4は、式(2)を、右辺の移流項である第1項の「−ui∂ρ/∂x|i」を削除して(省いて)使用し(式(4011)参照)、また、式(4)はそのまま使用する(式(4012)参照)(ステップS401)。
次に、演算部4は、式(13)を用いて、セミラグランジュ移流させた値であるρSLi,ΔtおよびρSLi,Δt/2を取得する(ステップS402)。
【0037】
続いて、演算部4は、式(4031)と式(4032)によって、k1,i(k1)とm1,i+1/2(m1)を求める。ここで、∂u/∂x|iはuの補間関数(説明を省略)から求めることができる。Δtは、時刻「n」と時刻「n+1」の差の時間長である。
【0038】
次に、演算部4は、式(4041)と式(4042)によって、ρ*i(ρn+1iの暫定値)とρ-X,*i+1/2(ρ-X,n+1i+1/2の暫定値)を取得する(ステップS404)。ここで、k1とm1はステップS403で取得された値であり、ρSLi,Δt/2はステップS402で取得された値である。
【0039】
続いて、演算部4は、式(4051)と式(4052)によって、k2,iとm2,i+1/2を取得する(ステップS405)。ここで、ρ*i(ρ*i+1も同様)は、ステップS404で取得された値である。また、∂u/∂x|i,∂2ρ*/∂x2|i,∂ρ*/∂x|iなどは、中心補間によって求められる。
【0040】
以下、演算部4は、同様にして、ステップS406〜ステップS409の演算を行うことによって、k1,i〜k4,i,m1,i+1/2〜m4,i+1/2のすべての値を取得することができる。なお、ステップS406およびステップS408において、ρ*iおよびρ-X,*i+1/2はそれぞれ新たに更新される。
そして、演算部4は、ステップS409までの演算で得た各値と式(4101)と式(4102)によって、ρn+1iとρ-X,n+1i+1/2を取得する(ステップS410)。
このようにして、第1実施形態の数値計算装置10によれば、保存形IDO法における偏微分方程式に対して部分的に(2つのうち片方の方程式に)セミラグランジュ法を適用することで、時間更新を行うことができる。
【0041】
次に、図5および図6を参照しながら、第1実施形態の数値計算装置による数値計算方法の計算結果例について説明する。図5は、第1実施形態の数値計算装置による数値計算方法の計算結果例を示すグラフである。ここでは、実際に爆発実験を行い、大気圧に対する加圧(量)に関して、実測値(実験データ)、第1実施形態による計算結果、および、比較例による計算結果の三者を比較した。
【0042】
図5に示すグラフにおいて、横軸は爆源からの距離(メートル)、縦軸は大気圧をゼロとした場合の加圧(パスカル)を表している。符号51の破線は、実験で得られた各距離の地点におけるピーク加圧の実測値を示す。符号51の破線を見れば、爆発による衝撃波が少しずつ弱まりながら遠方に伝搬していることがわかる。
【0043】
符号52の実線は、第1実施形態の部分セミラグ保存形IDO法により計算したある瞬間の衝撃波プロファイルである。そのピーク値が符号51の破線とほぼ一致しており、計算結果の精度が高いことがわかる。なお、この衝撃波プロファイルは、時間の経過とともに、その形をほぼ維持したまま右方に平行移動することになる。
一方、符号53の二点鎖線は、比較例の非保存形IDO法により計算したある瞬間の衝撃波プロファイルを示す。そのピーク値が符号51の破線と大きく離れており、計算結果の精度が第1実施形態の部分セミラグ保存形IDO法の場合よりも低いことがわかる。
【0044】
同じ実験に関する別のグラフについて、図6を参照しながら説明する。図6は、第1実施形態の数値計算装置による数値計算方法の計算結果例を示す両対数グラフである。ここでも、図5の場合と同様に、加圧に関して、実測値(実験データ)、第1実施形態による計算結果、および、比較例による計算結果の三者を比較した。
【0045】
図6に示す両対数グラフにおいて、横軸は爆源からの距離(メートル)、縦軸は大気圧をゼロとした場合のピーク加圧(パスカル)を表している。符号61の破線は、実験で得られた各距離の地点におけるピーク加圧の実測値を示す。符号61の破線を見れば、爆発による衝撃波が弱まりながら遠方に伝搬していることがわかる。
【0046】
符号62の実線は、第1実施形態の部分セミラグ保存形IDO法により計算したピーク加圧に関する衝撃波プロファイルを示す。符号62の実線は、符号61の破線とほぼ一致しており、計算結果の精度が高いことがわかる。
一方、符号63の二点鎖線は、比較例の非保存形IDO法により計算したピーク加圧に関する衝撃波プロファイルである。符号63の二点鎖線は、符号61の破線と大きく離れており、計算結果の精度が第1実施形態の部分セミラグ保存形IDO法の場合よりも低いことがわかる。
【0047】
つまり、図5および図6からわかるように、第1実施形態の部分セミラグ保存形IDO法によれば、比較例の非保存形IDO法の場合に比べて、爆源から近距離(たとえば10m程度)に関しても高い精度での計算結果を得ることができ、また、爆源から遠距離(たとえば200m以上)に関してはさらに高い精度での計算結果を得ることができる。
【0048】
このような第1実施形態の部分セミラグ保存形IDO法を応用すれば、車体周りの空気や熱の流れ、風力発電の空力解析、気象計算、津波予測など、多くの流体計算を高精度で行うことができる。また、爆発現象や、水と空気が混在する流れのような、空間的な密度変化が1000倍以上になる流体計算が可能となる。さらに、高速流体(高レイノルズ数流れ)で頻繁に発生する乱流に対し、定義された格子間隔よりも小さな渦による影響を渦粘性項無しでシミュレーションする、いわゆる陰的なラージ・エディ・シミュレーションになっていて、特別な乱流モデルを導入すること無しに複雑な流体計算を行うことができる。
【0049】
さらに説明すると、一般に、多くの利点を有している保存形IDO法の時間積分は、CIP法のようなセミラグランジュ法ではなく、オイラー法で解くためにルンゲクッタ法などが用いられる。しかし、通常のルンゲクッタ法を用いてアンダーシュート(プロファイルにおける下方への飛び出し誤差)やオーバーシュート(プロファイルにおける上方への飛び出し誤差)を抑制することは非常に難しい。そこで、ルンゲクッタ法による時間積分の各段階において、保存量となる積分値については従来の保存形IDO法による計算を行い、保存が保証されない格子点上の変数の時間積分に関する偏微分方程式を移流項と非移流項に分割し、セミラグランジュ法を適用し、さらに望ましくは後記するような単調性を有する補間関数を使用することで、アンダーシュートやオーバーシュートを抑制し、高い計算精度を実現することができる。
【0050】
(第2実施形態)
次に、本発明の第2実施形態について説明する。第2実施形態は、非保存形IDO法を用いた数値計算の例である。第2実施形態について説明する前に、その理解を助けるため、図11、図12Aおよび図12Bを参照しながら、非保存形IDO法を用いた数値計算の比較例(従来技術)について説明する。図11は、比較例の非保存形IDO法における変数イメージを示した図である。図12Aおよび図12Bは、比較例の非保存形IDO法におけるルンゲクッタ法による時間更新(時間積分)を示した図である。なお、以下、第1実施形態と重複する説明については適宜省略する。また、第2実施形態において、移流項における微分値の算出には風上補間を用い、非移流項における2階以上の微分値の算出には中心補間を用いる。
【0051】
比較例では、支配方程式として、拡散項を有する一次元質量保存の偏微分方程式である式(14)(式(1)と同様)を使用する。つまり、流体に関して、ρは密度、uは速度、tは時間、xは座標を表す変数である。なお、速度uを求めるための式が別に必要であるが、その記載を省略し、u,ux(uの一階微分)の値はその式などからすでに求められているものとする。
【数6】

【0052】
そして、実際に数値計算を行うことができるように、式(14)を変形して式(15)とする。
【数7】

【0053】
さらに、ρの微分値を式(16)と定義し、その微分値に関する方程式を式(17)と定義する。なお、∂ρx/∂x|iは、後記する補間関数(式(18))による風上補間によって求められる値である。また、非移流項における∂2u/∂x2|iおよび∂3ρ/∂x3|iは、中心補間によって求められる。
【数8】

【0054】
また、ρに関する補間関数を式(18)と定義する。式(19)〜(22)は、その拘束条件である。これらの式(19)〜(22)から、補間係数a〜dが式(23)〜(26)のように求められる。また、式(27)に示すように、ρiを二階微分した∂ρx/∂x|iは2bと等しくなる。
【数9】

【0055】
このような条件の下で、図12Aおよび図12Bに示したように、ルンゲクッタ法による時間更新(時間積分)を行う。ここでの目的は、時刻「n」における密度(ρni)と各係数(k1,i〜k4,i)から時刻「n+1」における密度(ρn+1i)を求めること(式(1215)参照)と、時刻「n」における密度の微分値(ρnx,i)と各係数(m1,i〜m4,i)から時刻「n+1」における密度(ρn+1x,i)を求めること(式(1216)参照)である。式(1201)〜式(1214)は、各係数(k1,i〜k4,i,m1,i〜m4,i)を求めるための式である。
【0056】
まず、式(1201)と式(1202)によって、k1,i(以下、「k1」とも表記する。k2,i〜k4,iについても同様)とm1,i(以下、「m1」とも表記する。m2,i〜m4,iについても同様)を求める。ここで、ui,ux,i,ρiおよびρx,iは、時刻「n」における値としてすでに求められている値を使用することができる。また、前記したように、移流項における∂ρ/∂x|iと∂ρx/∂x|iは風上補間により求めることができる。さらに、非移流項における∂2ρ/∂x2|i,∂2u/∂x2|iおよび∂3ρ/∂x3|iは、中心補間によって求められる。Δtは、時刻「n」と時刻「n+1」の差の時間長である。
【0057】
次に、式(1203)と式(1204)によって、ρ*i(ρn+1iの暫定値)とρ*x,i(ρn+1x,iの暫定値)を求める。ここで、ρiとρx,iは、時刻「n」における値としてすでに求められている値を使用することができる。また、k1とm1は、それぞれ式(1201)と式(1202)で求められた値である。
【0058】
そして、式(1205)と式(1206)によって、k2,iとm2,iを求める。ここで、ρ*iは、式(1203)で求められた値である。また、∂ρ*/∂x|iは、式(1204)で求められたρ*x,iである。
∂ρ*x/∂x|iは、式(27)と式(24)から求められる値であり(式(27)の∂ρx/∂x|iに相当)、具体的には、式(24)において式(1203)と式(1204)から求められたρ*i,ρ*i-1,ρ*x,iおよびρ*x,i-1を代入し、それによって得られたbに2を乗算することで求められる。また、非移流項における∂2ρ*/∂x2|i,∂2u/∂x2|iおよび∂3ρ*/∂x3|iは、中心補間によって求められる。
【0059】
以下、同様にして、式(1207)〜式(1214)を使うことにより、k1,i〜k4,i,m1,i〜m4,iの値をすべて求めることができる。そして、前記したように、式(1215)と式(1216)を使って、ρn+1iとρn+1x,iを求めることができる。なお、式(1207)と式(1211)においてρ*iは新たに更新され、式(1208)と式(1212)においてρ*x,iは新たに更新される。
【0060】
次に、図7および図8A〜図8Cを参照しながら、本発明の第2実施形態であるセミラグ非保存形IDO法(セミラグランジュ法を適用した非保存形IDO法)について説明する。
第2実施形態では、計算に、前記した比較例の場合と同じ式(14)〜式(26)を使用するので、重複説明を適宜省略する。なお、第2実施形態は、式(15)における右辺の移流項である第1項の「−uiρx,i」と、式(17)における右辺の移流項である第1項の「−ui∂ρx/∂x|i」とに関してセミラグランジュ移流を行う点で、比較例における計算と異なっている。
【0061】
第2実施形態では、式(18)に対して、X=xi−uiΔtを代入することで、Δtの分だけセミラグランジュ移流したρの値であるρSLi,Δtを算出することができる(式(28)参照)。なお、Fni(X),an,bn,cnおよびdnは、時刻「n」におけるそれぞれの値であることを意味している。また、式(28)におけるΔtをΔt/2と置き換えることで、Δt/2の分だけセミラグランジュ移流したρの値であるρSLi,Δt/2を算出することができる。
【数10】

【0062】
また、式(18)を微分した式(説明を省略)に対して、X=xi−uiΔtを代入することで、Δtの分だけセミラグランジュ移流したρx,iの値であるρSLx,i,Δtを算出することができる(式(29)参照)。また、式(29)におけるΔtをΔt/2と置き換えることで、Δt/2の分だけセミラグランジュ移流したρx,iの値であるρSLx,i,Δt/2を算出することができる。
【数11】

【0063】
ここで、図7は、第2実施形態のセミラグ非保存形IDO法における変数イメージを示した図である。図7に示したように、このρSLi,Δt(ρSLi,Δt/2)およびρSLx,i,Δt(ρSLx,i,Δt/2)の値を用いて、時刻「n+1」における密度(ρn+1i)を求めることができる(詳細は後記)。
【0064】
次に、図8A〜図8Cを参照しながら、第2実施形態における数値計算装置の演算(処理)について説明する(適宜他図参照)。図8A〜図8Cは、第2実施形態における数値計算装置の演算を示したフローチャートである。数値計算装置10の演算部4は、記憶部2とメモリ3を使用しながら各演算を行う。そして、この演算の目的は、比較例の場合と同様、時刻「n」における密度(ρi)やその微分値(ρx,i)などに基づいて、時刻「n+1」における密度(ρn+1i)と微分値(ρn+1x,i)を求めることである(ステップS430参照)。つまり、比較例の場合と同様、時刻「n」におけるρi,ρx,i,ux,iなどの値はすでに求められているものとして以下の演算を行う。なお、非移流項における∂2ρ/∂x2|i,∂2u/∂x2|iおよび∂3ρ/∂x3|iは、中心補間によって求められる。
【0065】
演算部4は、式(15)について右辺の移流項である第1項の「−uiρx,i」を削除して(省いて)使用し(式(4211)参照)、また、式(17)について右辺の移流項である第1項の「−ui∂ρx/∂x|i」を削除して(省いて)使用する(式(4212)参照)(ステップS421)。
次に、演算部4は、式(28)および式(29)を用いて、セミラグランジュ移流させた値であるρSLi,Δt,ρSLi,Δt/2,ρSLx,i,ΔtおよびρSLx,i,Δt/2を取得する(ステップS422)。
【0066】
続いて、演算部4は、式(4231)と式(4232)によって、k1,i(k1)とm1,i(m1)を求める。ここで、∂2ρ/∂x2|i,∂2u/∂x2|iおよび∂3ρ/∂x3|iは、中心補間によって求められる。Δtは、時刻「n」と時刻「n+1」の差の時間長である。
【0067】
次に、演算部4は、式(4241)と式(4242)によって、ρ*i(ρn+1iの暫定値)とρ*x,i(ρn+1x,iの暫定値)を取得する(ステップS424)。ここで、k1とm1はステップS423で取得された値であり、ρSLi,Δt/2およびρSLx,i,Δt/2はステップS422で取得された値である。
【0068】
続いて、演算部4は、式(4251)と式(4252)によって、k2,iとm2,iを取得する(ステップS425)。ここで、ρ*iおよびρ*x,iは、ステップS424で取得された値である。また、∂2ρ*/∂x2|i,∂2u/∂x2|iおよび∂3ρ*/∂x3|iは、中心補間によって求められる。
【0069】
以下、演算部4は、同様にして、ステップS426〜ステップS429の演算を行うことによって、k1,i〜k4,i,m1,i〜m4,iのすべての値を取得することができる。なお、ステップS426およびステップS428において、ρ*iおよびρ*x,iはそれぞれ新たに更新される。
そして、演算部4は、ステップS429までの演算で得た各値と式(4301)と式(4302)によって、ρn+1iとρn+1x,iを取得する(ステップS430)。
【0070】
このようにして、第2実施形態の数値計算装置10によれば、非保存形IDO法における偏微分方程式に対してセミラグランジュ法を適用することで、時間更新を行うことができる。また、その詳細な効果についての説明を省略するが、図5および図6を参照して説明した第1実施形態の場合と同様の効果を得ることができる。
【0071】
(変形例)
第1実施形態では、補間関数として、式(5)に示した式を使用した場合について説明したが、それ以外に、式(30)に示す分母に関数を有する有理関数を使用してもよい。β,aおよびcは、拘束条件により決定される係数である。
【数12】

【0072】
また、第2実施形態では、補間関数として、式(18)に示した式を使用した場合について説明したが、それ以外に、式(31)に示す分母に関数を有する有理関数を使用してもよい。a,b,cおよびdは、拘束条件により決定される係数である。
【数13】

そして、αとBは、数値計算の諸条件により、式(31)が単調性を有するように決定すればよい。たとえば、α=1とし、Bを式(32)および式(33)により決定すればよい。
【数14】

【0073】
このような式(30)や式(31)に示すように、単調性を有する(単調増加または単調減少する)補間関数を使用すれば、密度比や圧力比などが極端に大きな(たとえば1000倍以上)現象について数値計算を行う場合でも、その計算精度を高く維持することができる。つまり、密度比や圧力比などが極端に大きな現象に関する数値計算を行う場合、変数の数値の大きな場面での誤差の影響が大きくなる。そのため、単調性を有する補間関数を使用することで、急激な空間勾配のプロファイルに対してアンダーシュートやオーバーシュートをなくし、計算を安定させ、高い精度を維持することができるようになる。
【0074】
図13の(a)は、前記した2つの比較例においてκ(拡散係数)=0の場合の計算結果のプロファイルの例を示した図である。図13の(a)に示すように、比較例による計算結果(ドット)は、解析解(実線)に対してアンダーシュートやオーバーシュートを起こすことがあった。つまり、比較例では、密度比や圧力比などが極端に大きな現象についての数値計算が破綻することがあった。
【0075】
図13の(b)は、本実施形態(第1実施形態および第2実施形態に前記変形例の補間関数を適用したもの)においてκ(拡散係数)=0の場合の計算結果のプロファイルの例を示した図である。図13の(b)に示すように、本実施形態において上記のような有理関数を用いた場合の計算結果(ドット)は、解析解(実線)に対してアンダーシュートやオーバーシュートを起こすことがなくなる。つまり、本実施形態では、密度比や圧力比などが極端に大きな現象についての数値計算が安定するという効果を奏する。
なお、単調性を有する補間関数として、式(30)および式(31)を示したが、これらに限定されるものではない。
【0076】
また、当業者であれば、前記した各実施形態とその変形例にかかる数値計算方法をコンピュータに実行させるためのプログラムを作成し、さらに、そのプログラムをCD(Compact Disc)やDVD(Digital Versatile Disk)などの記録媒体に記録することができる。
【0077】
以上で本実施形態の説明を終えるが、本発明の態様はこれらに限定されるものではない。
たとえば、本実施形態では、説明を簡潔にするため、一次元空間の偏微分方程式について説明したが、2次元以上の空間の偏微分方程式を使用してもかまわない。
また、流体の変数として、密度を中心に説明したが、速度、圧力、温度などの別の変数に関しても同様に、本発明のセミラグランジュ移流による数値計算を適用することができる。
【0078】
さらに、時間積分のルンゲクッタ法については、4段で行う手法について説明したが、2段や3段など別の手法で行うようにしてもよい。
その他、数値計算装置や各フローチャートなどの具体的な構成について、本発明の趣旨を逸脱しない範囲で適宜変更が可能である。
【図面の簡単な説明】
【0079】
【図1】数値計算装置の構成図である。
【図2】流体の数値計算の演算の大まかな流れを表わしたフローチャートである。
【図3】第1実施形態の部分セミラグ保存形IDO法における変数イメージを示した図である。
【図4A】第1実施形態における数値計算装置の演算を示したフローチャートである。
【図4B】第1実施形態における数値計算装置の演算を示したフローチャートである。
【図4C】第1実施形態における数値計算装置の演算を示したフローチャートである。
【図5】第1実施形態の数値計算装置による数値計算方法の計算結果例を示すグラフである。
【図6】第1実施形態の数値計算装置による数値計算方法の計算結果例を示す両対数グラフである。
【図7】第2実施形態のセミラグ非保存形IDO法における変数イメージを示した図である。
【図8A】第2実施形態における数値計算装置の演算を示したフローチャートである。
【図8B】第2実施形態における数値計算装置の演算を示したフローチャートである。
【図8C】第2実施形態における数値計算装置の演算を示したフローチャートである。
【図9】比較例の保存形IDO法における変数イメージを示した図である。
【図10A】比較例の保存形IDO法におけるルンゲクッタ法による時間更新(時間積分)を示した図である。
【図10B】比較例の保存形IDO法におけるルンゲクッタ法による時間更新(時間積分)を示した図である。
【図11】比較例の非保存形IDO法における変数イメージを示した図である。
【図12A】比較例の非保存形IDO法におけるルンゲクッタ法による時間更新(時間積分)を示した図である。
【図12B】比較例の非保存形IDO法におけるルンゲクッタ法による時間更新(時間積分)を示した図である。
【図13】(a)は、比較例による計算結果のプロファイルの例を示した図であり、(b)は、本実施形態による計算結果のプロファイルの例を示した図である。
【符号の説明】
【0080】
1 入力部
2 記憶部
3 メモリ
4 演算部
5 出力部
10 数値計算装置
【技術分野】
【0001】
本発明は、偏微分方程式の演算に使用する数値計算方法、プログラムおよび記録媒体に関する。
【背景技術】
【0002】
近年、流体(液体や気体など)、電磁波、熱などに関する数値計算(シミュレーション)についての研究や開発が活発になってきている。
そのような数値計算を行う場合、流体などの変数(速度、圧力、温度、密度など)に関する偏微分方程式を、離散化された空間および時間に関して解く、という手法が用いられるのが一般的である。なぜなら、偏微分方程式の数学的な解析解(厳密解)を求めることは現実的に不可能だからである。したがって、高精度の数値計算方法を開発することが重要となる。
【0003】
そして、より高精度な計算を行うため、変数の値だけでなく変数の微分係数(空間勾配)の値も従属変数とするマルチモーメント手法であるCIP法(Cubic-Interpolated Pseudo-Particle Scheme)やIDO法(Interpolated Differential Operator Scheme:局所補間微分オペレータ法)が開発された。
【0004】
IDO法は、物理的に保存しなければならない質量、運動量、エネルギーを厳密に保存する保存形IDO法と、高精度数値計算の範囲内で物理的な保存を満足する非保存形IDO法とに大別することができる。保存形IDO法は、たとえば、変数の区間積分値(以下、単に「積分値」という。)を従属変数とすることで、その変数に関する物理量を保存することができる。
【0005】
そして、一般的に、計算の精度は保存形IDO法のほうがよい。しかし、保存形IDO法は値や積分値の定義点が異なるためにプログラムが複雑になるのに対し、非保存形IDO法は値と微分値が同じ格子点上に定義されるため、プログラムの構造が簡単になり境界条件も取り扱い易くなる。つまり、保存形IDO法と非保存形IDO法は、それぞれ一長一短を有し、場面や状況に応じて選択および使用される。
【0006】
そして、本出願人は、特許文献1において、非保存形IDO法における変数間の安定化カップリングの技術について提案した。この技術によれば、非保存形IDO法における数値計算の精度を向上させることができる。
【特許文献1】特開2006−318355号公報
【発明の開示】
【発明が解決しようとする課題】
【0007】
しかしながら、特許文献1の技術は、非保存形IDO法に使用するものであり、保存形IDO法に使用することはできない。つまり、保存形IDO法の計算精度の向上には、特許文献1の技術とは別の技術が必要となる。
そこで、本発明は、前記問題点に鑑みてなされたものであり、保存形IDO法を含めたIDO法に適用することで計算精度を向上させることができる数値計算方法、プログラムおよび記録媒体を提供することを目的とする。
【課題を解決するための手段】
【0008】
前記課題を解決するために、本発明は、複数の定義点における1つ以上の変数とその微分係数を含んだ複数の値を用いて偏微分方程式に関する演算を行い、変数のうち少なくともいずれか1つの変数を時間積分することにより、流体に関する数値計算を行う局所補間微分オペレータ法を実行する数値計算装置による数値計算方法である。
数値計算装置は、記憶部と演算部を有し、記憶部は、時間積分を行う変数の値と、その変数に関する補間関数とを記憶する。
そして、演算部は、偏微分方程式に関して、時間軸上の固定点以外の流動点による影響も考慮した方程式解法であるラグランジュ法を移流項に適用するセミラグランジュ移流を、補間関数を使って偏微分方程式の移流項に対して行うことで時間積分を行う。
また、当該数値計算方法をコンピュータに実行させるためのプログラムを作成し、さらに、そのプログラムを記録媒体に記録することができる。
【発明の効果】
【0009】
本発明によれば、保存形IDO法を含めたIDO法において、計算精度を向上させることができる。
【発明を実施するための最良の形態】
【0010】
以下、本発明の各実施形態について、適宜図面を参照しながら説明する。なお、本実施形態において、方程式の解法のうち、時間軸上の固定点に基づく解法をオイラー法といい、時間軸上の固定点以外の流動点による影響も考慮した解法をラグランジュ法という。また、偏微分方程式において、移流項にラグランジュ法を適用し、非移流項にオイラー法を適用する解法のことをセミラグランジュ(「セミラグ」と略記することもある。)法という。さらに、移流項に対してラグランジュ法を適用することを、「セミラグランジュ移流する(を行う)」と呼ぶ。ここで、移流項とは、ある物理量の局所変化を考える際に、対象物(流体など)自体の移動速度ベクトルとその物理量(またはその物理量の空間勾配)の空間勾配の内積に負の符号をつけた項のことを指す。また、移流項以外の項を非移流項という。
【0011】
図1および図2は各実施形態の説明に共通であり、まず、図1を参照しながら、数値計算方法を行う数値計算装置の構成について説明する。図1は、数値計算装置の構成図である。
数値計算装置10は、入力部1、記憶部2、メモリ3、演算部4および出力部5を備えて構成されるコンピュータ装置であり、たとえば、パソコン、ワークステーション、スーパーコンピュータなどにより実現することができる。
なお、演算部4は、ここでは1つとしているが、複数設けることにより並列計算を行うようにしてもよい。
【0012】
入力部1は、数値計算装置10の使用者(以下、単に「使用者」という)が各種情報を入力する手段であり、たとえば、キーボード、マウスなどである。
記憶部2は、各種情報を記憶するものであり、たとえば、ROM(Read Only Memory)、ハードディスクなどである。記憶部2は、ここでは、流体の数値計算(シミュレーション)を行うために、数値計算を行う場所を示す定義点である格子点、物理量(変数)やその微分係数の初期条件、支配方程式(自然現象を表わす偏微分方程式など)、補間関数、各種プログラムなどを記憶している。
【0013】
メモリ3は、演算部4が使用する一時記憶手段であり、たとえば、RAM(Random Access Memory)などである。
演算部4は、記憶部2に記憶された各種情報(プログラム、データなど)などに基づいて演算(処理)を行うものであり、たとえば、CPU(Central Processing Unit)である。
出力部5は、演算部4による演算の結果を出力するものであり、たとえば、ディスプレイなどである。
【0014】
次に、図2を参照しながら、数値計算の演算について説明する(適宜図1参照)。図2は、流体の数値計算の演算の大まかな流れを表わしたフローチャートである。
【0015】
まず、使用者が入力部1によって数値計算の開始に関する操作を行うと、演算部4は、記憶部2に記憶された情報に基づいて、演算を行う場所を示す定義点である格子点、各物理量の初期条件などを設定する(ステップS1)。
格子点は、たとえば、1次元の場合は「128」、2次元の場合は「32×32」、3次元の場合は「16×16×8」、といったように設定される。また、各物理量の初期条件としては、それぞれの格子点における変数の値、および、それらの値の微分係数(空間勾配)などが設定される。変数としては、たとえば、流体の速度、圧力、温度、密度などが挙げられる。
【0016】
次に、演算部4は、記憶部2に記憶された情報に基づいて、時間と空間に関する偏微分方程式などからなる支配方程式、各物理量の値を修正するための補間関数などを設定する(ステップS2)。
支配方程式としては、たとえば、圧縮性流体の運動方程式、流体の質量保存方程式などが挙げられ、詳細については後記する。また、補間関数としては、2次関数、3次関数、分母に関数を有する有理関数などが挙げられ、詳細については後記する。
【0017】
続いて、演算部4は、ステップS1およびステップS2で設定した各種情報を用い、時刻「t」における各格子点での各物理量の値に基づいて、時刻「t+1」における各格子点での各物理量の値を算出する、という演算をt=0,1,2,・・・nに関して行う(ステップS3〜ステップS5)。
そして、このステップS4における演算が本発明のポイントであるが、その詳細については後記する。
【0018】
次に、演算部4は、ステップS3〜ステップS5で算出した各物理量の値を、出力部5に出力する(ステップS6)。以上で、数値計算が完了する。
【0019】
(第1実施形態)
続いて、本発明の第1実施形態について説明する。第1実施形態は、保存形IDO法を用いた数値計算の例である。第1実施形態について説明する前に、その理解を助けるため、図9、図10Aおよび図10Bを参照しながら、保存形IDO法を用いた数値計算の比較例(従来技術)について説明する。図9は、比較例の保存形IDO法における変数イメージを示した図である。図10Aおよび図10Bは、比較例の保存形IDO法におけるルンゲクッタ法による時間更新(時間積分)を示した図である。
【0020】
なお、第1実施形態において、移流項における微分値の算出には風上補間(2つの格子点のうち風下側(流れの下流側)の格子点を中心にして行う補間)を用い、非移流項における微分値の算出には中心補間(3つの格子点のうちの真ん中の格子点を中心にして行う補間)を用いる。
【0021】
比較例では、支配方程式として、拡散項を有する一次元質量保存の偏微分方程式である式(1)を使用する。なお、流体に関して、ρは密度、uは速度、tは時間、xは座標を表す変数である。また、κ(カッパ)は拡散係数(物質の拡散の度合を示す係数)であり、あらかじめ与えられる。なお、速度uを求めるための式が別に必要であるが、その記載を省略し、速度uはその式によってすでに求められているものとする。
【数1】

【0022】
そして、実際に数値計算を行うことができるように、式(1)を変形して式(2)とする。なお、式(2)において「i」が付与された各変数は、複数の格子点のうち「i」番目の格子点上の変数であることを意味する。また、∂ρ/∂x|iは補間関数を用いた風上補間から求められる値である(詳細は後記)。さらに、∂u/∂x|iおよび∂2ρ/∂x2|iは補間関数を用いた中心補間から求められる値である(詳細は後記)。なお、本実施形態において、右側に「|i」が付与された項は、「座標「i」における、補間関数を用いて算出される値」であることを意味する。
【数2】

【0023】
さらに、ρの積分値を式(3)と定義し、その積分値に関する方程式を式(4)と定義する。なお、式(3)において記載されている「i+1/2」は、積分区間の両端(「i」と「i+1」)の中間地点を表している。また、式(4)において、「i+1」が付与された各変数は「i+1」番目の格子点上の変数であることを意味する。
【数3】

【0024】
また、∂ρ/∂x|iの風上補間に用いられる補間関数を式(5)と定義する。式(6)〜(8)は、その拘束条件である。これらの式(5)〜(8)から、補間係数a,bおよびcが式(9)〜(11)のように求められる。また、式(12)に示したように、ρiを微分したρx,i(=∂ρ/∂x|i)はbと等しくなる。
【数4】

【0025】
このような条件の下で、図10Aおよび図10Bに示したように、ルンゲクッタ法による時間更新(時間積分)を行う。ここでの目的は、時刻「n」における密度(ρni)と各係数(k1,i〜k4,i)から時刻「n+1」における密度(ρn+1i)を求めること(式(1015)参照)と、時刻「n」における密度の積分値(ρ-X,ni+1/2)と各係数(m1,i+1/2〜m4,i+1/2)から時刻「n+1」における密度(ρ-X,n+1i+1/2)を求めること(式(1016)参照)である。式(1001)〜式(1014)は、各係数(k1,i〜k4,i,m1,i+1/2〜m4,i+1/2)を求めるための式である。
【0026】
まず、式(1001)と式(1002)によって、k1,i(以下、「k1」とも表記する。k2,i〜k4,iについても同様)とm1,i+1/2(以下、「m1」とも表記する。m2,i+1/2〜m4,i+1/2についても同様)を求める。ここで、ui,ui+1,ρi,ρi+1の値は、時刻「n」における値としてすでに求められているものを使用することができる。なお、移流項である「−ui∂ρ/∂x|i」における「∂ρ/∂x|i」は、前記したように風上補間によって求めることができる。
【0027】
また、∂u/∂x|iはuの補間関数から求めることができる。ここでは、たとえば、uの補間関数として4次関数を使用し、中心補間によって∂u/∂x|iを求めることができる。その場合、3つの格子点の座標を「i-1」,「i」および「i+1」とし、補間関数をf(X)、その積分値(前記式(8)と同様)をfX(X)すると、その補間関数は、f(i-1),f(i),f(i+1),fX(i-1/2)およびfX(i+1/2)の拘束条件から決定することができる。∂2ρ/∂x2|iおよび非移流項中の∂ρ/∂x|iについても、同様にして中心補間から求めることができる。
【0028】
Δtは、時刻「n」と時刻「n+1」の差の時間長(時間刻み幅)である。なお、この式(1001)と式(1002)によって演算が行われる段階では、すべての格子点に関して演算が行われ、その後、次の演算に進む。以降についても同様である。
【0029】
次に、式(1003)と式(1004)によって、ρ*i(ρn+1iの暫定値)とρ-X,*i+1/2(ρ-X,n+1i+1/2の暫定値)を求める。ここで、ρi,ρ-Xi+1/2は、時刻「n」における値としてすでに求められているものを使用することができる。また、k1とm1は、それぞれ式(1001)と式(1002)で求められた値である。
【0030】
そして、式(1005)と式(1006)によって、k2,iとm2,i+1/2を求める。ここで、ρ*i(ρ*i+1も同様)は、式(1003)で求められた値である。また、移流項における∂ρ*/∂x|i(ρ*x,i)は、式(12)からbであることがわかり、前記した式(10)の右辺に、式(1003)と式(1004)から求められたρ*i,ρ*i-1,ρ-X,*i-1/2を代入することにより求められる。また、∂2ρ*/∂x2|iおよび非移流項中の∂ρ*/∂x|iについては、中心補間から求めることができる。
【0031】
以下、同様にして、式(1007)〜式(1014)を使うことにより、k1,i〜k4,i,m1,i+1/2〜m4,i+1/2の値をすべて求めることができる。そして、前記したように、式(1015)と式(1016)を使って、ρn+1iとρ-X,n+1i+1/2を求めることができる。なお、式(1007)と式(1011)においてρ*iは新たに更新され、式(1008)と式(1012)においてρ-X,*i+1/2は新たに更新される。
【0032】
次に、図3〜図6を参照しながら、本発明の第1実施形態の部分セミラグ保存形IDO法(セミラグランジュ法を部分的に適用した保存形IDO法)について説明する。
第1実施形態では、計算に、前記した比較例の場合と同じ式(1)〜式(11)を使用するので、重複説明を適宜省略する。なお、第1実施形態は、式(2)における右辺の移流項である第1項の「−ui∂ρ/∂x|i」に関してセミラグランジュ移流を行う点で、比較例における計算と異なっている。
【0033】
第1実施形態では、式(5)に対して、X=xi−uiΔtを代入することで、Δtの分だけセミラグランジュ移流したρの値であるρSLi,Δtを算出することができる(式(13)参照)。なお、式(13)において、Fni(X),anおよびbnは、時刻「n」におけるそれぞれの値であることを意味している。また、式(13)におけるΔtをΔt/2と置き換えることで、Δt/2の分だけセミラグランジュ移流したρの値であるρSLi,Δt/2を算出することができる。
【数5】

【0034】
ここで、図3は、第1実施形態の部分セミラグ保存形IDO法における変数イメージを示した図である。図3に示したように、このρSLi,Δtの値を用いて、時刻「n+1」における密度(ρn+1i)を求めることができる(詳細は後記)。
【0035】
次に、図4A〜図4Cを参照しながら、第1実施形態における数値計算装置の演算(処理)について説明する(適宜他図参照)。図4A〜図4Cは、第1実施形態における数値計算装置の演算を示したフローチャートである。数値計算装置10の演算部4は、記憶部2とメモリ3を使用しながら各演算を行う。そして、この演算の目的は、比較例の場合と同様、時刻「n」における密度(ρi)やその積分値(ρ-Xi+1/2(ρ-X,ni+1/2))などに基づいて、時刻「n+1」における密度(ρn+1i)と積分値(ρ-X,n+1i+1/2)を求めることである(ステップS410参照)。つまり、比較例の場合と同様、時刻「n」におけるρi,ρ-Xi+1/2,ui,ui+1,ρi,ρi+1などの値はすでに求められているものとして、以下の演算を行う。また、∂u/∂x|i,∂2ρ/∂x2|i,∂ρ/∂x|iなどは、前記した比較例の場合と同様、中心補間によって求められる。
【0036】
演算部4は、式(2)を、右辺の移流項である第1項の「−ui∂ρ/∂x|i」を削除して(省いて)使用し(式(4011)参照)、また、式(4)はそのまま使用する(式(4012)参照)(ステップS401)。
次に、演算部4は、式(13)を用いて、セミラグランジュ移流させた値であるρSLi,ΔtおよびρSLi,Δt/2を取得する(ステップS402)。
【0037】
続いて、演算部4は、式(4031)と式(4032)によって、k1,i(k1)とm1,i+1/2(m1)を求める。ここで、∂u/∂x|iはuの補間関数(説明を省略)から求めることができる。Δtは、時刻「n」と時刻「n+1」の差の時間長である。
【0038】
次に、演算部4は、式(4041)と式(4042)によって、ρ*i(ρn+1iの暫定値)とρ-X,*i+1/2(ρ-X,n+1i+1/2の暫定値)を取得する(ステップS404)。ここで、k1とm1はステップS403で取得された値であり、ρSLi,Δt/2はステップS402で取得された値である。
【0039】
続いて、演算部4は、式(4051)と式(4052)によって、k2,iとm2,i+1/2を取得する(ステップS405)。ここで、ρ*i(ρ*i+1も同様)は、ステップS404で取得された値である。また、∂u/∂x|i,∂2ρ*/∂x2|i,∂ρ*/∂x|iなどは、中心補間によって求められる。
【0040】
以下、演算部4は、同様にして、ステップS406〜ステップS409の演算を行うことによって、k1,i〜k4,i,m1,i+1/2〜m4,i+1/2のすべての値を取得することができる。なお、ステップS406およびステップS408において、ρ*iおよびρ-X,*i+1/2はそれぞれ新たに更新される。
そして、演算部4は、ステップS409までの演算で得た各値と式(4101)と式(4102)によって、ρn+1iとρ-X,n+1i+1/2を取得する(ステップS410)。
このようにして、第1実施形態の数値計算装置10によれば、保存形IDO法における偏微分方程式に対して部分的に(2つのうち片方の方程式に)セミラグランジュ法を適用することで、時間更新を行うことができる。
【0041】
次に、図5および図6を参照しながら、第1実施形態の数値計算装置による数値計算方法の計算結果例について説明する。図5は、第1実施形態の数値計算装置による数値計算方法の計算結果例を示すグラフである。ここでは、実際に爆発実験を行い、大気圧に対する加圧(量)に関して、実測値(実験データ)、第1実施形態による計算結果、および、比較例による計算結果の三者を比較した。
【0042】
図5に示すグラフにおいて、横軸は爆源からの距離(メートル)、縦軸は大気圧をゼロとした場合の加圧(パスカル)を表している。符号51の破線は、実験で得られた各距離の地点におけるピーク加圧の実測値を示す。符号51の破線を見れば、爆発による衝撃波が少しずつ弱まりながら遠方に伝搬していることがわかる。
【0043】
符号52の実線は、第1実施形態の部分セミラグ保存形IDO法により計算したある瞬間の衝撃波プロファイルである。そのピーク値が符号51の破線とほぼ一致しており、計算結果の精度が高いことがわかる。なお、この衝撃波プロファイルは、時間の経過とともに、その形をほぼ維持したまま右方に平行移動することになる。
一方、符号53の二点鎖線は、比較例の非保存形IDO法により計算したある瞬間の衝撃波プロファイルを示す。そのピーク値が符号51の破線と大きく離れており、計算結果の精度が第1実施形態の部分セミラグ保存形IDO法の場合よりも低いことがわかる。
【0044】
同じ実験に関する別のグラフについて、図6を参照しながら説明する。図6は、第1実施形態の数値計算装置による数値計算方法の計算結果例を示す両対数グラフである。ここでも、図5の場合と同様に、加圧に関して、実測値(実験データ)、第1実施形態による計算結果、および、比較例による計算結果の三者を比較した。
【0045】
図6に示す両対数グラフにおいて、横軸は爆源からの距離(メートル)、縦軸は大気圧をゼロとした場合のピーク加圧(パスカル)を表している。符号61の破線は、実験で得られた各距離の地点におけるピーク加圧の実測値を示す。符号61の破線を見れば、爆発による衝撃波が弱まりながら遠方に伝搬していることがわかる。
【0046】
符号62の実線は、第1実施形態の部分セミラグ保存形IDO法により計算したピーク加圧に関する衝撃波プロファイルを示す。符号62の実線は、符号61の破線とほぼ一致しており、計算結果の精度が高いことがわかる。
一方、符号63の二点鎖線は、比較例の非保存形IDO法により計算したピーク加圧に関する衝撃波プロファイルである。符号63の二点鎖線は、符号61の破線と大きく離れており、計算結果の精度が第1実施形態の部分セミラグ保存形IDO法の場合よりも低いことがわかる。
【0047】
つまり、図5および図6からわかるように、第1実施形態の部分セミラグ保存形IDO法によれば、比較例の非保存形IDO法の場合に比べて、爆源から近距離(たとえば10m程度)に関しても高い精度での計算結果を得ることができ、また、爆源から遠距離(たとえば200m以上)に関してはさらに高い精度での計算結果を得ることができる。
【0048】
このような第1実施形態の部分セミラグ保存形IDO法を応用すれば、車体周りの空気や熱の流れ、風力発電の空力解析、気象計算、津波予測など、多くの流体計算を高精度で行うことができる。また、爆発現象や、水と空気が混在する流れのような、空間的な密度変化が1000倍以上になる流体計算が可能となる。さらに、高速流体(高レイノルズ数流れ)で頻繁に発生する乱流に対し、定義された格子間隔よりも小さな渦による影響を渦粘性項無しでシミュレーションする、いわゆる陰的なラージ・エディ・シミュレーションになっていて、特別な乱流モデルを導入すること無しに複雑な流体計算を行うことができる。
【0049】
さらに説明すると、一般に、多くの利点を有している保存形IDO法の時間積分は、CIP法のようなセミラグランジュ法ではなく、オイラー法で解くためにルンゲクッタ法などが用いられる。しかし、通常のルンゲクッタ法を用いてアンダーシュート(プロファイルにおける下方への飛び出し誤差)やオーバーシュート(プロファイルにおける上方への飛び出し誤差)を抑制することは非常に難しい。そこで、ルンゲクッタ法による時間積分の各段階において、保存量となる積分値については従来の保存形IDO法による計算を行い、保存が保証されない格子点上の変数の時間積分に関する偏微分方程式を移流項と非移流項に分割し、セミラグランジュ法を適用し、さらに望ましくは後記するような単調性を有する補間関数を使用することで、アンダーシュートやオーバーシュートを抑制し、高い計算精度を実現することができる。
【0050】
(第2実施形態)
次に、本発明の第2実施形態について説明する。第2実施形態は、非保存形IDO法を用いた数値計算の例である。第2実施形態について説明する前に、その理解を助けるため、図11、図12Aおよび図12Bを参照しながら、非保存形IDO法を用いた数値計算の比較例(従来技術)について説明する。図11は、比較例の非保存形IDO法における変数イメージを示した図である。図12Aおよび図12Bは、比較例の非保存形IDO法におけるルンゲクッタ法による時間更新(時間積分)を示した図である。なお、以下、第1実施形態と重複する説明については適宜省略する。また、第2実施形態において、移流項における微分値の算出には風上補間を用い、非移流項における2階以上の微分値の算出には中心補間を用いる。
【0051】
比較例では、支配方程式として、拡散項を有する一次元質量保存の偏微分方程式である式(14)(式(1)と同様)を使用する。つまり、流体に関して、ρは密度、uは速度、tは時間、xは座標を表す変数である。なお、速度uを求めるための式が別に必要であるが、その記載を省略し、u,ux(uの一階微分)の値はその式などからすでに求められているものとする。
【数6】

【0052】
そして、実際に数値計算を行うことができるように、式(14)を変形して式(15)とする。
【数7】

【0053】
さらに、ρの微分値を式(16)と定義し、その微分値に関する方程式を式(17)と定義する。なお、∂ρx/∂x|iは、後記する補間関数(式(18))による風上補間によって求められる値である。また、非移流項における∂2u/∂x2|iおよび∂3ρ/∂x3|iは、中心補間によって求められる。
【数8】

【0054】
また、ρに関する補間関数を式(18)と定義する。式(19)〜(22)は、その拘束条件である。これらの式(19)〜(22)から、補間係数a〜dが式(23)〜(26)のように求められる。また、式(27)に示すように、ρiを二階微分した∂ρx/∂x|iは2bと等しくなる。
【数9】

【0055】
このような条件の下で、図12Aおよび図12Bに示したように、ルンゲクッタ法による時間更新(時間積分)を行う。ここでの目的は、時刻「n」における密度(ρni)と各係数(k1,i〜k4,i)から時刻「n+1」における密度(ρn+1i)を求めること(式(1215)参照)と、時刻「n」における密度の微分値(ρnx,i)と各係数(m1,i〜m4,i)から時刻「n+1」における密度(ρn+1x,i)を求めること(式(1216)参照)である。式(1201)〜式(1214)は、各係数(k1,i〜k4,i,m1,i〜m4,i)を求めるための式である。
【0056】
まず、式(1201)と式(1202)によって、k1,i(以下、「k1」とも表記する。k2,i〜k4,iについても同様)とm1,i(以下、「m1」とも表記する。m2,i〜m4,iについても同様)を求める。ここで、ui,ux,i,ρiおよびρx,iは、時刻「n」における値としてすでに求められている値を使用することができる。また、前記したように、移流項における∂ρ/∂x|iと∂ρx/∂x|iは風上補間により求めることができる。さらに、非移流項における∂2ρ/∂x2|i,∂2u/∂x2|iおよび∂3ρ/∂x3|iは、中心補間によって求められる。Δtは、時刻「n」と時刻「n+1」の差の時間長である。
【0057】
次に、式(1203)と式(1204)によって、ρ*i(ρn+1iの暫定値)とρ*x,i(ρn+1x,iの暫定値)を求める。ここで、ρiとρx,iは、時刻「n」における値としてすでに求められている値を使用することができる。また、k1とm1は、それぞれ式(1201)と式(1202)で求められた値である。
【0058】
そして、式(1205)と式(1206)によって、k2,iとm2,iを求める。ここで、ρ*iは、式(1203)で求められた値である。また、∂ρ*/∂x|iは、式(1204)で求められたρ*x,iである。
∂ρ*x/∂x|iは、式(27)と式(24)から求められる値であり(式(27)の∂ρx/∂x|iに相当)、具体的には、式(24)において式(1203)と式(1204)から求められたρ*i,ρ*i-1,ρ*x,iおよびρ*x,i-1を代入し、それによって得られたbに2を乗算することで求められる。また、非移流項における∂2ρ*/∂x2|i,∂2u/∂x2|iおよび∂3ρ*/∂x3|iは、中心補間によって求められる。
【0059】
以下、同様にして、式(1207)〜式(1214)を使うことにより、k1,i〜k4,i,m1,i〜m4,iの値をすべて求めることができる。そして、前記したように、式(1215)と式(1216)を使って、ρn+1iとρn+1x,iを求めることができる。なお、式(1207)と式(1211)においてρ*iは新たに更新され、式(1208)と式(1212)においてρ*x,iは新たに更新される。
【0060】
次に、図7および図8A〜図8Cを参照しながら、本発明の第2実施形態であるセミラグ非保存形IDO法(セミラグランジュ法を適用した非保存形IDO法)について説明する。
第2実施形態では、計算に、前記した比較例の場合と同じ式(14)〜式(26)を使用するので、重複説明を適宜省略する。なお、第2実施形態は、式(15)における右辺の移流項である第1項の「−uiρx,i」と、式(17)における右辺の移流項である第1項の「−ui∂ρx/∂x|i」とに関してセミラグランジュ移流を行う点で、比較例における計算と異なっている。
【0061】
第2実施形態では、式(18)に対して、X=xi−uiΔtを代入することで、Δtの分だけセミラグランジュ移流したρの値であるρSLi,Δtを算出することができる(式(28)参照)。なお、Fni(X),an,bn,cnおよびdnは、時刻「n」におけるそれぞれの値であることを意味している。また、式(28)におけるΔtをΔt/2と置き換えることで、Δt/2の分だけセミラグランジュ移流したρの値であるρSLi,Δt/2を算出することができる。
【数10】

【0062】
また、式(18)を微分した式(説明を省略)に対して、X=xi−uiΔtを代入することで、Δtの分だけセミラグランジュ移流したρx,iの値であるρSLx,i,Δtを算出することができる(式(29)参照)。また、式(29)におけるΔtをΔt/2と置き換えることで、Δt/2の分だけセミラグランジュ移流したρx,iの値であるρSLx,i,Δt/2を算出することができる。
【数11】

【0063】
ここで、図7は、第2実施形態のセミラグ非保存形IDO法における変数イメージを示した図である。図7に示したように、このρSLi,Δt(ρSLi,Δt/2)およびρSLx,i,Δt(ρSLx,i,Δt/2)の値を用いて、時刻「n+1」における密度(ρn+1i)を求めることができる(詳細は後記)。
【0064】
次に、図8A〜図8Cを参照しながら、第2実施形態における数値計算装置の演算(処理)について説明する(適宜他図参照)。図8A〜図8Cは、第2実施形態における数値計算装置の演算を示したフローチャートである。数値計算装置10の演算部4は、記憶部2とメモリ3を使用しながら各演算を行う。そして、この演算の目的は、比較例の場合と同様、時刻「n」における密度(ρi)やその微分値(ρx,i)などに基づいて、時刻「n+1」における密度(ρn+1i)と微分値(ρn+1x,i)を求めることである(ステップS430参照)。つまり、比較例の場合と同様、時刻「n」におけるρi,ρx,i,ux,iなどの値はすでに求められているものとして以下の演算を行う。なお、非移流項における∂2ρ/∂x2|i,∂2u/∂x2|iおよび∂3ρ/∂x3|iは、中心補間によって求められる。
【0065】
演算部4は、式(15)について右辺の移流項である第1項の「−uiρx,i」を削除して(省いて)使用し(式(4211)参照)、また、式(17)について右辺の移流項である第1項の「−ui∂ρx/∂x|i」を削除して(省いて)使用する(式(4212)参照)(ステップS421)。
次に、演算部4は、式(28)および式(29)を用いて、セミラグランジュ移流させた値であるρSLi,Δt,ρSLi,Δt/2,ρSLx,i,ΔtおよびρSLx,i,Δt/2を取得する(ステップS422)。
【0066】
続いて、演算部4は、式(4231)と式(4232)によって、k1,i(k1)とm1,i(m1)を求める。ここで、∂2ρ/∂x2|i,∂2u/∂x2|iおよび∂3ρ/∂x3|iは、中心補間によって求められる。Δtは、時刻「n」と時刻「n+1」の差の時間長である。
【0067】
次に、演算部4は、式(4241)と式(4242)によって、ρ*i(ρn+1iの暫定値)とρ*x,i(ρn+1x,iの暫定値)を取得する(ステップS424)。ここで、k1とm1はステップS423で取得された値であり、ρSLi,Δt/2およびρSLx,i,Δt/2はステップS422で取得された値である。
【0068】
続いて、演算部4は、式(4251)と式(4252)によって、k2,iとm2,iを取得する(ステップS425)。ここで、ρ*iおよびρ*x,iは、ステップS424で取得された値である。また、∂2ρ*/∂x2|i,∂2u/∂x2|iおよび∂3ρ*/∂x3|iは、中心補間によって求められる。
【0069】
以下、演算部4は、同様にして、ステップS426〜ステップS429の演算を行うことによって、k1,i〜k4,i,m1,i〜m4,iのすべての値を取得することができる。なお、ステップS426およびステップS428において、ρ*iおよびρ*x,iはそれぞれ新たに更新される。
そして、演算部4は、ステップS429までの演算で得た各値と式(4301)と式(4302)によって、ρn+1iとρn+1x,iを取得する(ステップS430)。
【0070】
このようにして、第2実施形態の数値計算装置10によれば、非保存形IDO法における偏微分方程式に対してセミラグランジュ法を適用することで、時間更新を行うことができる。また、その詳細な効果についての説明を省略するが、図5および図6を参照して説明した第1実施形態の場合と同様の効果を得ることができる。
【0071】
(変形例)
第1実施形態では、補間関数として、式(5)に示した式を使用した場合について説明したが、それ以外に、式(30)に示す分母に関数を有する有理関数を使用してもよい。β,aおよびcは、拘束条件により決定される係数である。
【数12】

【0072】
また、第2実施形態では、補間関数として、式(18)に示した式を使用した場合について説明したが、それ以外に、式(31)に示す分母に関数を有する有理関数を使用してもよい。a,b,cおよびdは、拘束条件により決定される係数である。
【数13】

そして、αとBは、数値計算の諸条件により、式(31)が単調性を有するように決定すればよい。たとえば、α=1とし、Bを式(32)および式(33)により決定すればよい。
【数14】

【0073】
このような式(30)や式(31)に示すように、単調性を有する(単調増加または単調減少する)補間関数を使用すれば、密度比や圧力比などが極端に大きな(たとえば1000倍以上)現象について数値計算を行う場合でも、その計算精度を高く維持することができる。つまり、密度比や圧力比などが極端に大きな現象に関する数値計算を行う場合、変数の数値の大きな場面での誤差の影響が大きくなる。そのため、単調性を有する補間関数を使用することで、急激な空間勾配のプロファイルに対してアンダーシュートやオーバーシュートをなくし、計算を安定させ、高い精度を維持することができるようになる。
【0074】
図13の(a)は、前記した2つの比較例においてκ(拡散係数)=0の場合の計算結果のプロファイルの例を示した図である。図13の(a)に示すように、比較例による計算結果(ドット)は、解析解(実線)に対してアンダーシュートやオーバーシュートを起こすことがあった。つまり、比較例では、密度比や圧力比などが極端に大きな現象についての数値計算が破綻することがあった。
【0075】
図13の(b)は、本実施形態(第1実施形態および第2実施形態に前記変形例の補間関数を適用したもの)においてκ(拡散係数)=0の場合の計算結果のプロファイルの例を示した図である。図13の(b)に示すように、本実施形態において上記のような有理関数を用いた場合の計算結果(ドット)は、解析解(実線)に対してアンダーシュートやオーバーシュートを起こすことがなくなる。つまり、本実施形態では、密度比や圧力比などが極端に大きな現象についての数値計算が安定するという効果を奏する。
なお、単調性を有する補間関数として、式(30)および式(31)を示したが、これらに限定されるものではない。
【0076】
また、当業者であれば、前記した各実施形態とその変形例にかかる数値計算方法をコンピュータに実行させるためのプログラムを作成し、さらに、そのプログラムをCD(Compact Disc)やDVD(Digital Versatile Disk)などの記録媒体に記録することができる。
【0077】
以上で本実施形態の説明を終えるが、本発明の態様はこれらに限定されるものではない。
たとえば、本実施形態では、説明を簡潔にするため、一次元空間の偏微分方程式について説明したが、2次元以上の空間の偏微分方程式を使用してもかまわない。
また、流体の変数として、密度を中心に説明したが、速度、圧力、温度などの別の変数に関しても同様に、本発明のセミラグランジュ移流による数値計算を適用することができる。
【0078】
さらに、時間積分のルンゲクッタ法については、4段で行う手法について説明したが、2段や3段など別の手法で行うようにしてもよい。
その他、数値計算装置や各フローチャートなどの具体的な構成について、本発明の趣旨を逸脱しない範囲で適宜変更が可能である。
【図面の簡単な説明】
【0079】
【図1】数値計算装置の構成図である。
【図2】流体の数値計算の演算の大まかな流れを表わしたフローチャートである。
【図3】第1実施形態の部分セミラグ保存形IDO法における変数イメージを示した図である。
【図4A】第1実施形態における数値計算装置の演算を示したフローチャートである。
【図4B】第1実施形態における数値計算装置の演算を示したフローチャートである。
【図4C】第1実施形態における数値計算装置の演算を示したフローチャートである。
【図5】第1実施形態の数値計算装置による数値計算方法の計算結果例を示すグラフである。
【図6】第1実施形態の数値計算装置による数値計算方法の計算結果例を示す両対数グラフである。
【図7】第2実施形態のセミラグ非保存形IDO法における変数イメージを示した図である。
【図8A】第2実施形態における数値計算装置の演算を示したフローチャートである。
【図8B】第2実施形態における数値計算装置の演算を示したフローチャートである。
【図8C】第2実施形態における数値計算装置の演算を示したフローチャートである。
【図9】比較例の保存形IDO法における変数イメージを示した図である。
【図10A】比較例の保存形IDO法におけるルンゲクッタ法による時間更新(時間積分)を示した図である。
【図10B】比較例の保存形IDO法におけるルンゲクッタ法による時間更新(時間積分)を示した図である。
【図11】比較例の非保存形IDO法における変数イメージを示した図である。
【図12A】比較例の非保存形IDO法におけるルンゲクッタ法による時間更新(時間積分)を示した図である。
【図12B】比較例の非保存形IDO法におけるルンゲクッタ法による時間更新(時間積分)を示した図である。
【図13】(a)は、比較例による計算結果のプロファイルの例を示した図であり、(b)は、本実施形態による計算結果のプロファイルの例を示した図である。
【符号の説明】
【0080】
1 入力部
2 記憶部
3 メモリ
4 演算部
5 出力部
10 数値計算装置
【特許請求の範囲】
【請求項1】
複数の定義点における1つ以上の変数とその微分係数を含んだ複数の値を用いて偏微分方程式に関する演算を行い、前記変数のうち少なくともいずれか1つの変数を時間積分することにより、流体に関する数値計算を行う局所補間微分オペレータ法を実行する数値計算装置による数値計算方法であって、
前記数値計算装置は、記憶部と演算部を有し、
前記記憶部は、前記時間積分を行う変数の値と、その変数に関する補間関数と、を記憶し、
前記演算部は、前記偏微分方程式に関して、時間軸上の固定点以外の流動点による影響も考慮した方程式解法であるラグランジュ法を移流項に適用するセミラグランジュ移流を、前記補間関数を使って前記偏微分方程式の移流項に対して行うことで前記時間積分を行う
ことを特徴とする数値計算方法。
【請求項2】
前記局所補間微分オペレータ法は、前記時間積分を行う変数の区間積分値を保存する保存形局所補間微分オペレータ法であり、
前記演算部は、前記区間積分値を演算する場合には前記セミラグランジュ移流を行わず、前記時間積分を行う変数の値を演算する場合には前記セミラグランジュ移流を行うことで、前記時間積分を行う
ことを特徴とする請求項1に記載の数値計算方法。
【請求項3】
前記演算部は、ルンゲクッタ法によって前記時間積分を行う
ことを特徴とする請求項1または請求項2に記載の数値計算方法。
【請求項4】
前記補間関数は、単調増加または単調減少する有理関数である
ことを特徴とする請求項1から請求項3のいずれか一項に記載の数値計算方法。
【請求項5】
請求項1から請求項4のいずれか一項に記載の数値計算方法をコンピュータに実行させるためのプログラム。
【請求項6】
請求項5に記載のプログラムを記録した記録媒体。
【請求項1】
複数の定義点における1つ以上の変数とその微分係数を含んだ複数の値を用いて偏微分方程式に関する演算を行い、前記変数のうち少なくともいずれか1つの変数を時間積分することにより、流体に関する数値計算を行う局所補間微分オペレータ法を実行する数値計算装置による数値計算方法であって、
前記数値計算装置は、記憶部と演算部を有し、
前記記憶部は、前記時間積分を行う変数の値と、その変数に関する補間関数と、を記憶し、
前記演算部は、前記偏微分方程式に関して、時間軸上の固定点以外の流動点による影響も考慮した方程式解法であるラグランジュ法を移流項に適用するセミラグランジュ移流を、前記補間関数を使って前記偏微分方程式の移流項に対して行うことで前記時間積分を行う
ことを特徴とする数値計算方法。
【請求項2】
前記局所補間微分オペレータ法は、前記時間積分を行う変数の区間積分値を保存する保存形局所補間微分オペレータ法であり、
前記演算部は、前記区間積分値を演算する場合には前記セミラグランジュ移流を行わず、前記時間積分を行う変数の値を演算する場合には前記セミラグランジュ移流を行うことで、前記時間積分を行う
ことを特徴とする請求項1に記載の数値計算方法。
【請求項3】
前記演算部は、ルンゲクッタ法によって前記時間積分を行う
ことを特徴とする請求項1または請求項2に記載の数値計算方法。
【請求項4】
前記補間関数は、単調増加または単調減少する有理関数である
ことを特徴とする請求項1から請求項3のいずれか一項に記載の数値計算方法。
【請求項5】
請求項1から請求項4のいずれか一項に記載の数値計算方法をコンピュータに実行させるためのプログラム。
【請求項6】
請求項5に記載のプログラムを記録した記録媒体。
【図1】


【図2】


【図3】


【図4A】


【図4B】


【図4C】


【図5】


【図6】


【図7】


【図8A】


【図8B】


【図8C】


【図9】


【図10A】


【図10B】


【図11】


【図12A】


【図12B】


【図13】




【図2】


【図3】


【図4A】


【図4B】


【図4C】


【図5】


【図6】


【図7】


【図8A】


【図8B】


【図8C】


【図9】


【図10A】


【図10B】


【図11】


【図12A】


【図12B】


【図13】


【公開番号】特開2008−197949(P2008−197949A)
【公開日】平成20年8月28日(2008.8.28)
【国際特許分類】
【出願番号】特願2007−32967(P2007−32967)
【出願日】平成19年2月14日(2007.2.14)
【出願人】(304021417)国立大学法人東京工業大学 (1,821)
【Fターム(参考)】
【公開日】平成20年8月28日(2008.8.28)
【国際特許分類】
【出願日】平成19年2月14日(2007.2.14)
【出願人】(304021417)国立大学法人東京工業大学 (1,821)
【Fターム(参考)】
[ Back to top ]

