気液2相流解析方法
【課題】 多孔質構造体における2相浸透流れに対して均質化法を適用し、マルチスケール解析のための理論構築を図り、その数値解析アルゴリズムを提案することを提供すること。
【解決手段】 多孔質体構造体を流れる気液2相の流れをミクロ・マクロスケールで解析する気液2相流解析方法において、想定している立方体ミクロ構造で、3軸方向圧力勾配、及び水飽和度を変化させたときの、気相浸透係数Ka、液相透過係数Kw、及び毛管圧力Pcawをデータとして記憶し、多孔質体構造体の多孔質体形状を、データから読み出した気相浸透係数Ka、液相透過係数Kw、及び毛管圧力Pcawを持った等価均質体に置き換えて、マクロ構造の浸透流解析を行う。
【解決手段】 多孔質体構造体を流れる気液2相の流れをミクロ・マクロスケールで解析する気液2相流解析方法において、想定している立方体ミクロ構造で、3軸方向圧力勾配、及び水飽和度を変化させたときの、気相浸透係数Ka、液相透過係数Kw、及び毛管圧力Pcawをデータとして記憶し、多孔質体構造体の多孔質体形状を、データから読み出した気相浸透係数Ka、液相透過係数Kw、及び毛管圧力Pcawを持った等価均質体に置き換えて、マクロ構造の浸透流解析を行う。
【発明の詳細な説明】
【技術分野】
【0001】
この発明は、多孔質体構造体を流れる気液2相の流れをミクロ・マクロスケールで解析する気液2相流解析方法に関するものである。
【背景技術】
【0002】
例えば、燃料電池の開発においては、まずは拡散層における水の浸透現象を知ることが重要である。拡散層のような多孔質体における流れは、気相と液相の流体が存在する場合において、当該流れは複雑化する。その流れを解析する上で注意しなければならないのは図12 に示すように、多孔質体における浸透流れを着目するスケール(巨視スケールから微視スケールまで)によって全く異なる現象として捉えなければならないことである。
図12の(a)に示す最もスケールの大きい巨視スケールでは飽和度に斑を生じさせながら、徐々に液体の飽和度が高くなっていくような流れになる。このスケールにおいてはDarcy 則の浸透係数や拡散方程式の拡散係数といった現象に応じた係数を用いることで流体の移動を表現する。
図12の(b)に示す、より微視的なスケール(メゾスケール)で見た場合、相ごとに界面が生じ、表面張力や粘性が支配的になる。大抵の場合、液体は固体表面に張り付くような動きをし、比較的ゆっくりとした流れになると考えられる。
巨視スケール、メゾスケールにおいては連続体近似が成り立ち、運動量保存則はNavier Stokes 式である。
【0003】
多孔質体は無数の立方体ミクロ構造を持った非均質な材料と見ることが出来る。この非均質性を数値解析に導入しようとすると、立方体ミクロ構造の幾何性状や材料特性等の詳細な情報をすべて取り入れなくてはならない。このような直接的に立方体ミクロ構造を反映させた解析はモデル生成が困難な上に、立方体ミクロ構造の情報が時間によって変化するような非定常性や非線形性を含む場合、膨大な計算機資源を消費し、現実的な選択ではない。
従って、多孔質体内の気相と液相の浸透流れをミクロ・マクロのマルチスケールで現象を把握したい場合、それぞれのスケールを関係付けて何らかの平均化を導入した数理モデルが必要となる。
すなわち、ミクロスケールの構造や気相と液相の分布性状から、マクロスケールの流れの支配方程式や特性を導く方法論を構築し、直接的に解いて得られる流れの場と等価な現象を解析する必要がある。
その方法論の1 つが数学的均質化法であり、そこで導出される数理モデルを数値的に解く手法はマルチスケール解析手法と呼ばれている.
【0004】
すべての材料は、微視的に見れば複数の相からなる複合構造を有しており、各相の幾何学的及び物理的条件・各相間の相互作用によって、その巨視的物性が特徴づけられるというのが均質化法の思想である。均質化法の多くは構造解析に用いられることが多いが、流体解析においても同様の過程を経て、ミクロ・マクロスケールの支配方程式を導出することが出来る。その例として、 Terada et al. (非特許文献1) は多孔材料においてマクロスケールの支配方程式としてDarcy 則を導出し、固液連成現象のマルチスケール解析を行っている。
また、2相流に対しては例えばB. Amaziane et al. (非特許文献2) によって研究されている。
また、特許文献1には、マイクロ領域と、ミクロ領域とを設定し、マクロ領域における溶融物の凝固過程を演算し、その演算結果に基づきミクロ領域における溶融物の凝固過程を演算する工程が繰り返される凝固シミュレーション装置が開示されている。
【0005】
【非特許文献1】Terada, K., Ito, T. and Kikuchi, N. : Characterization of the mechanical behaviors of solid-fluid mixture by the homogenization, Comput. Methods Appl. Mech. Engrg., Vol. 153, pp. 223-257,1998.
【非特許文献2】AMAZIANE, B., BOURGEAT, A. and KOEBBE, J. : NUMERICAL SIMULATION AND HOMOGENIZATION OF TWO-PHASE FLOW IN HETEROGENEOUS POROUS MEDIA,Transport in Porous Media, Vol. 6, pp. 519-547, 1991.
【特許文献1】特開2003-39163号公報
【発明の開示】
【発明が解決しようとする課題】
【0006】
しかしながら、非特許文献1及び非特許文献2の技術は、ミクロ・マクロスケールを連成させて計算する方法であり、膨大な計算時間を必要とし、非効率である。また、特許文献1の技術は、ミクロ領域の演算精度を高めるものであり、ミクロ・マクロスケールの解析には、膨大な計算時間が必要とされるため、非効率である。
従来技術の計算方法では、例えば、100mm四方(厚さ1mm)の構造体に10μm四方の空孔を有するメッシュを作成すると、総メッシュ数は、100億メッシュとなり、ミクロ解析を行うだけで、数年規模の膨大な計算時間を必要とする問題がある。
【0007】
この発明は上記事情に鑑みてなされたものであって、多孔質構造体における2相浸透流れに対して均質化法を適用し、マルチスケール解析のための理論構築を図り、その数値解析アルゴリズムを提案することを提供することを目的とする。
【課題を解決するための手段】
【0008】
上記目的を達成するために、本発明の多孔質体構造体を流れる気液2相の流れをミクロ・マクロスケールで解析する気液2相流解析方法は、次の構成を有している。
(1)多孔質体構造体を流れる気液2相の流れをミクロ・マクロスケールで解析する気液2相流解析方法において、想定している立方体ミクロ構造で、3軸方向圧力勾配、及び水飽和度を変化させたときの、気相浸透係数Ka、液相透過係数Kw、及び毛管圧力Pcawをデータとして記憶し、多孔質体構造体の多孔質体形状を、データから読み出した気相浸透係数Ka、液相透過係数Kw、及び毛管圧力Pcawを持った等価均質体に置き換えて、マクロ構造の浸透流解析を行う。
(2)多孔質体構造体を流れる気液2相の流れをミクロ・マクロスケールで解析する気液2相流解析方法において、マクロ構造の浸透流解析結果のうち、詳細に評価したい箇所の3軸方向圧力勾配、及びマクロ構造水飽和度を求め、求めた3軸方向圧力勾配、及びマクロ構造水飽和度を立方体ミクロ構造に付与することにより、ミクロ解析を行う。
(3)多孔質体構造体を流れる気液2相の流れをミクロ・マクロスケールで解析する気液2相流解析方法において、想定している立方体ミクロ構造で、3軸方向圧力勾配及、び水飽和度を変化させたときの、気相浸透係数Ka、液相透過係数Kw、及び毛管圧力Pcawを関数近似し、その近似された関数を用いてマクロ構造の浸透流解析を行う。
【発明の効果】
【0009】
次に、上記構成を有する本発明の気液2相流解析方法の作用・効果について説明する。
本発明の気液2相流解析方法は、多孔質体構造体を流れる気液2相の流れをミクロ・マクロスケールで解析する気液2相流解析方法において、想定している立方体ミクロ構造で、3軸方向圧力勾配及び水飽和度を変化させたときの、気相浸透係数Ka、液相透過係数Kw、及び毛管圧力Pcawをデータとして記憶し、多孔質体構造体の多孔質体形状を、データから読み出した気相浸透係数Ka、液相透過係数Kw、及び毛管圧力Pcawを持った等価均質体に置き換えて、マクロ構造の浸透流解析を行うので、本来の均質化法に基づく非線形マルチスケール解析が、常にミクロスケールの分布性状とマクロスケールの分布性状が平衡状態を保ちながら、マクロスケールの変数を求めるといった非常に大掛かりな解析になるのに対して、本発明の解析はあくまでもマクロ解析のみであり、ミクロスケールの構造を意識する必要はないため、近似である点は精度の劣化が考えられるが、計算コストの面では利便性が高い。ここで、ミクロスケールの構造を意識する必要がないのは、既に浸透係数がミクロスケールの構造を近似したものとして算出されているからである。
【0010】
また、本発明の気液2相流解析方法は、多孔質体構造体を流れる気液2相の流れをミクロ・マクロスケールで解析する気液2相流解析方法において、マクロ構造の浸透流解析結果のうち、詳細に評価したい箇所の3軸方向圧力勾配、及びマクロ構造水飽和度を求め、求めた3軸方向圧力勾配、及びマクロ構造水飽和度を立方体ミクロ構造に付与することにより、ミクロ解析を行うので、必要とする箇所について、マクロ構造体の一部のミクロ構造体の気液2相流挙動を把握することができる。
【0011】
また、本発明の気液2相流解析は、多孔質体構造体を流れる気液2相の流れをミクロ・マクロスケールで解析する気液2相流解析方法において、想定している立方体ミクロ構造で、3軸方向圧力勾配、及び水飽和度を変化させたときの、気相浸透係数Ka、液相透過係数Kw、及び毛管圧力Pcawを関数近似し、その近似された関数を用いてマクロ構造の浸透流解析を行うので、関数近似を用いることで、非連成でマクロ構造及びミクロ構造を解析できるため、ミクロ構造を繰り返すことによる計算コストを必要とせず、計算コストを低減することができる。
【発明を実施するための最良の形態】
【0012】
以下、本発明の気相と液相の2相流解析方法の一実施形態について図面を参照して詳細に説明する。
【0013】
(ステップ1)立方体ミクロ構造において、水飽和度Sw、及び3軸方向圧力勾配を変化させて、2相流計算を実施する。
ミクロ構造として、図1に示す想定空間11を想定する。想定空間11は、一辺の長さが、50μmの立方体であり、中心位置に水飽和度Swに応じた大きさの立方体形状の水12が存在する。想定空間11の対向する2面間毎に、すなわちXYZの3軸の軸毎に圧力勾配▽Px、▽Py、▽Pzを仮定する。
液相の飽和度Swについては、0 から1 までのミクロスケールの相の分布として、図2に示す11個のパターンを設定する。すなわち、水飽和度Swは、0%から100%まで、10%ずつ増加する、図2に示す11段階を設定する。
【0014】
【数1】

ここで、ρは密度であり、vαは、Y−periodicな特性流速であり、μは粘性係数であり、pはミクロ構造内の圧力であり、Pはマクロ構造内の圧力であり、fは外力であり、▽は微分であり、下付きのαは相を表し、Γは固体表面を表している。
モデルとして図1に示す解析条件の下で、ミクロ構造支配方程式である(数1)の4つの式を解き、|Y| 、Yαを求める。
一方、kαは、(数2)から求められる。
【数2】

【0015】
(ステップ2)ステップ1で得られた値を(数3)の右辺に代入することにより、気相透過係数Ka、液相透過係数Kw、及び毛管圧力Pcawを算出する。
【数3】

ここで、Kαは、透過係数であり、Kaは気相透過係数であり、Kwは液相透過係数であり、各々が3方向のベクトルである。kは特性流速であり、dyはミクロ構造微小領域であり、Yはミクロ領域であり、|Y| はミクロ構造体積である。また、Pcawは毛管圧力であり、Paは気相圧力であり、Pwは液相圧力である。
【0016】
図1に示すモデルにおける、気相の透過係数Ka、液相の透過係数Kw、毛管圧力Pcawのデータを図3、4、5に示す。いずれも横軸は、水飽和度Swである。図3の縦軸は、気相の透過係数Kaである。図4の縦軸は、液相の透過係数Kwである。図5の縦軸は、毛管圧力Pcawである。
ここで、(数4)に示すように、Pcaw、Ka、Kwを、水飽和度Sw、圧力勾配▽Pの
関数として関数近似しても良い。関数近似した値を図3、4、5に実線で示す。○印はデータを示す。
【数4】

【0017】
(ステップ3)多孔体形状を、ステップ2で得られた図3、4、5のマップデータの特性を持った等価均質体に置き換え、マクロ構造の浸透流解析を実施する。
すなわち、(数5)に示すマクロ構造支配方程式に、Kα、Pcawをマップデータに基づいた値を代入することにより、計算される。この計算は、市販の汎用流体解析ソフトFLUENTを使用した。実用面での利便性が高いFLUENT では、Darcy 則を抵抗の効果として運動方程式に導入している。
【数5】

上記ミクロ解析で求めたデータの近似関数、またはデータマップを用いてマクロ解析を行う。
【0018】
マクロ解析の例として図6 に示す解析条件の問題を考える。横100mm、縦300mm、厚さ0.5mmのマクロ構造体を考える。下面が流入口23,24で、上面が流出口25であり、両側面は壁であると仮定する。入口の中央部20mm幅に水の流入口24がある。水の流入速度は、0.2m/secとする。水の流入口24の両側に各々30mm幅に空気の流入口23が形成されている。空気の流入速度は、0.3m/secとする。流出口25における圧力は、0Paである。
【0019】
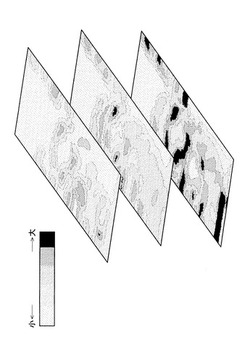
ステップ3のマクロ構造の浸透流解析した結果を、図7に示す。また、水12の分布を図8に示す。図8に示した3枚の図は、下から、底面、中間面、上面における水12の存在を示している。濃い部分は、水12が多く存在することを示している。また、空気の分布を図9に示す。図9に示した3枚の図は、下から、底面、中間面、上面における空気の存在を示している。濃い部分は、空気が多く存在することを示している。また、図10に水12及び空気の速度分布を示す。図10に示した3枚の図は、下から、底面、中間面、上面における水及び空気の速度分布を示している。濃い部分は、水及び空気の速度が速いことを示している。
【0020】
以上、詳細に説明したように、本実施例の気液2相流解析方法によれば、多孔体構造体を流れる気液2相の流れをミクロ・マクロスケールで解析する気液2相流解析方法において、想定している立方体ミクロ構造で、3方向圧力勾配及び水飽和度を変化させたときの、浸透係数及び毛管圧力をデータとして記憶し、多孔体構造体の多孔体形状を、データから読み出した浸透係数及び毛管圧力を持った等価均質体に置き換えて、マクロ構造の浸透流解析を行うので、本来の均質化法に基づく非線形マルチスケール解析が、常にミクロスケールの分布性状とマクロスケールの分布性状が平衡状態を保ちながら、マクロスケールの変数を求めるといった非常に大掛かりな解析になるのに対して、本発明の解析はあくまでもマクロ解析のみであり、ミクロスケールの構造を意識する必要はないため、近似である点は精度の劣化が考えられるが、計算コストの面では利便性が高い。ここで、ミクロスケールの構造を意識する必要がないのは、既に浸透係数がミクロスケールの構造を近似したものとして算出されているからである。
【0021】
また、本実施例の気液2相流解析方法によれば、多孔体構造体を流れる気液2相の流れをミクロ・マクロスケールで解析する気液2相流解析方法において、想定している立方体ミクロ構造で、3方向圧力勾配及び水飽和度を変化させたときの、浸透係数及び毛管圧力を関数近似し、その近似された関数を用いてマクロ構造の浸透流解析を行うので、関数近似を用いることで、非連成でマクロ構造及びミクロ構造を解析できるため、ミクロ構造を繰り返すことによる計算コストを必要とせず、計算コストを低減することができる。
すなわち、従来は、ミクロ構造計算した結果を、逐一マクロ構造の浸透流解析にフィードバックしてマクロ構造計算を行い、次のミクロ構造計算を行うという、いわゆる練成計算を行っているため、計算時間が多くかかっていた。それに対して、本実施例では、マクロ解析から、水飽和度Sw、3軸の圧力勾配▽Px、▽Py、▽Pzを用いて、一方的にミクロ構造計算を行い、KαとPcawを関数近似式として求め、その関数近似式を用いて、マクロ構造の浸透流解析を行っているので、逐一ミクロ構造計算を行う必要のない、いわゆる非連成解析アルゴリズムを用いるため、ミクロ解析とマクロ解析とを完全に分離して計算でき、計算時間を短縮することができる。
【0022】
次に、本発明の第2の実施例について説明する。第2の実施例は、第1実施例で得られた図8、9、10の図のうち、詳細なデータを必要とする箇所を図中で指摘することにより、指摘された部分に関して、ミクロ構造体の気液2相流分布を算出するステップを追加したものである。
すなわち、指摘された箇所の立方体ミクロ構造に関して、3軸方向の圧力勾配▽Px、▽Py、▽Pz、及び水飽和度Swを、図8、9、10に示したマクロ構造の浸透流解析結果より求めて、その値を(数1)のミクロ構造支配方程式に代入することにより、ミクロ構造体における水12の分布を得ることができる。得られた分布を図11に示す。想定空間11内で、水12が、分散した状態を示している。濃い色の部分13は、水12が多く存在する部分であり、白色部分15は、水12が存在しない部分であり、薄い色の部分14は、その中間部分である。
【0023】
以上説明したように、第2実施例の気液2相流解析方法によれば、多孔体構造体を流れる気液2相の流れをミクロ・マクロスケールで解析する気液2相流解析方法において、マクロ構造の浸透流解析結果のうち、詳細に評価したい箇所の3方向圧力勾配及びマクロ構造水飽和度を求め、求めた3方向圧力勾配及びマクロ構造水飽和度を立方体ミクロ構造に付与することにより、ミクロ解析を行うので、必要とする箇所について、マクロ構造体の一部のミクロ構造体の気液2相流挙動を把握することができる。
【0024】
このように多孔質体内のミクロ構造を反映したマクロ的な浸透特性を評価した上で,2相浸透流解析を行えば燃料電池の拡散層の水分管理を意図した設計支援が可能となりうる.特に,ミクロ構造内部の幾何性状を設計変数にとることでマクロ特性をコントロールしたり,またマクロ境界条件を変数にとることで飽和度の最適分布を探索する行程の構築するなど燃料電池のCAE における利用価値は高まると考えられる.
【0025】
なお、この発明は前記実施形態に限定されるものではなく、発明の趣旨を逸脱することのない範囲で構成の一部を適宜変更して実施することもできる。
【図面の簡単な説明】
【0026】
【図1】立体ミクロ構造として想定した想定空間11を示す図である。
【図2】水飽和度Swの11のパターンを示す図である。
【図3】気相の透過係数Kaのデータ図である。
【図4】液相の透過係数Kwのデータ図である。
【図5】毛管圧力Pcawのデータ図である。
【図6】マクロ解析の解析条件を示す図である。
【図7】マクロ構造の浸透流解析した結果を示す図である。
【図8】水12の分布を示す図である。
【図9】空気の分布を示す図である。
【図10】水12と空気の速度の分布を示す図である。
【図11】ミクロ構造体における水12の分布を示す図である。
【図12】巨視スケールから微視スケールで気液2相流の流れを模式化した図である。
【符号の説明】
【0027】
11 立方体ミクロ構造
12 水
【技術分野】
【0001】
この発明は、多孔質体構造体を流れる気液2相の流れをミクロ・マクロスケールで解析する気液2相流解析方法に関するものである。
【背景技術】
【0002】
例えば、燃料電池の開発においては、まずは拡散層における水の浸透現象を知ることが重要である。拡散層のような多孔質体における流れは、気相と液相の流体が存在する場合において、当該流れは複雑化する。その流れを解析する上で注意しなければならないのは図12 に示すように、多孔質体における浸透流れを着目するスケール(巨視スケールから微視スケールまで)によって全く異なる現象として捉えなければならないことである。
図12の(a)に示す最もスケールの大きい巨視スケールでは飽和度に斑を生じさせながら、徐々に液体の飽和度が高くなっていくような流れになる。このスケールにおいてはDarcy 則の浸透係数や拡散方程式の拡散係数といった現象に応じた係数を用いることで流体の移動を表現する。
図12の(b)に示す、より微視的なスケール(メゾスケール)で見た場合、相ごとに界面が生じ、表面張力や粘性が支配的になる。大抵の場合、液体は固体表面に張り付くような動きをし、比較的ゆっくりとした流れになると考えられる。
巨視スケール、メゾスケールにおいては連続体近似が成り立ち、運動量保存則はNavier Stokes 式である。
【0003】
多孔質体は無数の立方体ミクロ構造を持った非均質な材料と見ることが出来る。この非均質性を数値解析に導入しようとすると、立方体ミクロ構造の幾何性状や材料特性等の詳細な情報をすべて取り入れなくてはならない。このような直接的に立方体ミクロ構造を反映させた解析はモデル生成が困難な上に、立方体ミクロ構造の情報が時間によって変化するような非定常性や非線形性を含む場合、膨大な計算機資源を消費し、現実的な選択ではない。
従って、多孔質体内の気相と液相の浸透流れをミクロ・マクロのマルチスケールで現象を把握したい場合、それぞれのスケールを関係付けて何らかの平均化を導入した数理モデルが必要となる。
すなわち、ミクロスケールの構造や気相と液相の分布性状から、マクロスケールの流れの支配方程式や特性を導く方法論を構築し、直接的に解いて得られる流れの場と等価な現象を解析する必要がある。
その方法論の1 つが数学的均質化法であり、そこで導出される数理モデルを数値的に解く手法はマルチスケール解析手法と呼ばれている.
【0004】
すべての材料は、微視的に見れば複数の相からなる複合構造を有しており、各相の幾何学的及び物理的条件・各相間の相互作用によって、その巨視的物性が特徴づけられるというのが均質化法の思想である。均質化法の多くは構造解析に用いられることが多いが、流体解析においても同様の過程を経て、ミクロ・マクロスケールの支配方程式を導出することが出来る。その例として、 Terada et al. (非特許文献1) は多孔材料においてマクロスケールの支配方程式としてDarcy 則を導出し、固液連成現象のマルチスケール解析を行っている。
また、2相流に対しては例えばB. Amaziane et al. (非特許文献2) によって研究されている。
また、特許文献1には、マイクロ領域と、ミクロ領域とを設定し、マクロ領域における溶融物の凝固過程を演算し、その演算結果に基づきミクロ領域における溶融物の凝固過程を演算する工程が繰り返される凝固シミュレーション装置が開示されている。
【0005】
【非特許文献1】Terada, K., Ito, T. and Kikuchi, N. : Characterization of the mechanical behaviors of solid-fluid mixture by the homogenization, Comput. Methods Appl. Mech. Engrg., Vol. 153, pp. 223-257,1998.
【非特許文献2】AMAZIANE, B., BOURGEAT, A. and KOEBBE, J. : NUMERICAL SIMULATION AND HOMOGENIZATION OF TWO-PHASE FLOW IN HETEROGENEOUS POROUS MEDIA,Transport in Porous Media, Vol. 6, pp. 519-547, 1991.
【特許文献1】特開2003-39163号公報
【発明の開示】
【発明が解決しようとする課題】
【0006】
しかしながら、非特許文献1及び非特許文献2の技術は、ミクロ・マクロスケールを連成させて計算する方法であり、膨大な計算時間を必要とし、非効率である。また、特許文献1の技術は、ミクロ領域の演算精度を高めるものであり、ミクロ・マクロスケールの解析には、膨大な計算時間が必要とされるため、非効率である。
従来技術の計算方法では、例えば、100mm四方(厚さ1mm)の構造体に10μm四方の空孔を有するメッシュを作成すると、総メッシュ数は、100億メッシュとなり、ミクロ解析を行うだけで、数年規模の膨大な計算時間を必要とする問題がある。
【0007】
この発明は上記事情に鑑みてなされたものであって、多孔質構造体における2相浸透流れに対して均質化法を適用し、マルチスケール解析のための理論構築を図り、その数値解析アルゴリズムを提案することを提供することを目的とする。
【課題を解決するための手段】
【0008】
上記目的を達成するために、本発明の多孔質体構造体を流れる気液2相の流れをミクロ・マクロスケールで解析する気液2相流解析方法は、次の構成を有している。
(1)多孔質体構造体を流れる気液2相の流れをミクロ・マクロスケールで解析する気液2相流解析方法において、想定している立方体ミクロ構造で、3軸方向圧力勾配、及び水飽和度を変化させたときの、気相浸透係数Ka、液相透過係数Kw、及び毛管圧力Pcawをデータとして記憶し、多孔質体構造体の多孔質体形状を、データから読み出した気相浸透係数Ka、液相透過係数Kw、及び毛管圧力Pcawを持った等価均質体に置き換えて、マクロ構造の浸透流解析を行う。
(2)多孔質体構造体を流れる気液2相の流れをミクロ・マクロスケールで解析する気液2相流解析方法において、マクロ構造の浸透流解析結果のうち、詳細に評価したい箇所の3軸方向圧力勾配、及びマクロ構造水飽和度を求め、求めた3軸方向圧力勾配、及びマクロ構造水飽和度を立方体ミクロ構造に付与することにより、ミクロ解析を行う。
(3)多孔質体構造体を流れる気液2相の流れをミクロ・マクロスケールで解析する気液2相流解析方法において、想定している立方体ミクロ構造で、3軸方向圧力勾配及、び水飽和度を変化させたときの、気相浸透係数Ka、液相透過係数Kw、及び毛管圧力Pcawを関数近似し、その近似された関数を用いてマクロ構造の浸透流解析を行う。
【発明の効果】
【0009】
次に、上記構成を有する本発明の気液2相流解析方法の作用・効果について説明する。
本発明の気液2相流解析方法は、多孔質体構造体を流れる気液2相の流れをミクロ・マクロスケールで解析する気液2相流解析方法において、想定している立方体ミクロ構造で、3軸方向圧力勾配及び水飽和度を変化させたときの、気相浸透係数Ka、液相透過係数Kw、及び毛管圧力Pcawをデータとして記憶し、多孔質体構造体の多孔質体形状を、データから読み出した気相浸透係数Ka、液相透過係数Kw、及び毛管圧力Pcawを持った等価均質体に置き換えて、マクロ構造の浸透流解析を行うので、本来の均質化法に基づく非線形マルチスケール解析が、常にミクロスケールの分布性状とマクロスケールの分布性状が平衡状態を保ちながら、マクロスケールの変数を求めるといった非常に大掛かりな解析になるのに対して、本発明の解析はあくまでもマクロ解析のみであり、ミクロスケールの構造を意識する必要はないため、近似である点は精度の劣化が考えられるが、計算コストの面では利便性が高い。ここで、ミクロスケールの構造を意識する必要がないのは、既に浸透係数がミクロスケールの構造を近似したものとして算出されているからである。
【0010】
また、本発明の気液2相流解析方法は、多孔質体構造体を流れる気液2相の流れをミクロ・マクロスケールで解析する気液2相流解析方法において、マクロ構造の浸透流解析結果のうち、詳細に評価したい箇所の3軸方向圧力勾配、及びマクロ構造水飽和度を求め、求めた3軸方向圧力勾配、及びマクロ構造水飽和度を立方体ミクロ構造に付与することにより、ミクロ解析を行うので、必要とする箇所について、マクロ構造体の一部のミクロ構造体の気液2相流挙動を把握することができる。
【0011】
また、本発明の気液2相流解析は、多孔質体構造体を流れる気液2相の流れをミクロ・マクロスケールで解析する気液2相流解析方法において、想定している立方体ミクロ構造で、3軸方向圧力勾配、及び水飽和度を変化させたときの、気相浸透係数Ka、液相透過係数Kw、及び毛管圧力Pcawを関数近似し、その近似された関数を用いてマクロ構造の浸透流解析を行うので、関数近似を用いることで、非連成でマクロ構造及びミクロ構造を解析できるため、ミクロ構造を繰り返すことによる計算コストを必要とせず、計算コストを低減することができる。
【発明を実施するための最良の形態】
【0012】
以下、本発明の気相と液相の2相流解析方法の一実施形態について図面を参照して詳細に説明する。
【0013】
(ステップ1)立方体ミクロ構造において、水飽和度Sw、及び3軸方向圧力勾配を変化させて、2相流計算を実施する。
ミクロ構造として、図1に示す想定空間11を想定する。想定空間11は、一辺の長さが、50μmの立方体であり、中心位置に水飽和度Swに応じた大きさの立方体形状の水12が存在する。想定空間11の対向する2面間毎に、すなわちXYZの3軸の軸毎に圧力勾配▽Px、▽Py、▽Pzを仮定する。
液相の飽和度Swについては、0 から1 までのミクロスケールの相の分布として、図2に示す11個のパターンを設定する。すなわち、水飽和度Swは、0%から100%まで、10%ずつ増加する、図2に示す11段階を設定する。
【0014】
【数1】

ここで、ρは密度であり、vαは、Y−periodicな特性流速であり、μは粘性係数であり、pはミクロ構造内の圧力であり、Pはマクロ構造内の圧力であり、fは外力であり、▽は微分であり、下付きのαは相を表し、Γは固体表面を表している。
モデルとして図1に示す解析条件の下で、ミクロ構造支配方程式である(数1)の4つの式を解き、|Y| 、Yαを求める。
一方、kαは、(数2)から求められる。
【数2】

【0015】
(ステップ2)ステップ1で得られた値を(数3)の右辺に代入することにより、気相透過係数Ka、液相透過係数Kw、及び毛管圧力Pcawを算出する。
【数3】

ここで、Kαは、透過係数であり、Kaは気相透過係数であり、Kwは液相透過係数であり、各々が3方向のベクトルである。kは特性流速であり、dyはミクロ構造微小領域であり、Yはミクロ領域であり、|Y| はミクロ構造体積である。また、Pcawは毛管圧力であり、Paは気相圧力であり、Pwは液相圧力である。
【0016】
図1に示すモデルにおける、気相の透過係数Ka、液相の透過係数Kw、毛管圧力Pcawのデータを図3、4、5に示す。いずれも横軸は、水飽和度Swである。図3の縦軸は、気相の透過係数Kaである。図4の縦軸は、液相の透過係数Kwである。図5の縦軸は、毛管圧力Pcawである。
ここで、(数4)に示すように、Pcaw、Ka、Kwを、水飽和度Sw、圧力勾配▽Pの
関数として関数近似しても良い。関数近似した値を図3、4、5に実線で示す。○印はデータを示す。
【数4】

【0017】
(ステップ3)多孔体形状を、ステップ2で得られた図3、4、5のマップデータの特性を持った等価均質体に置き換え、マクロ構造の浸透流解析を実施する。
すなわち、(数5)に示すマクロ構造支配方程式に、Kα、Pcawをマップデータに基づいた値を代入することにより、計算される。この計算は、市販の汎用流体解析ソフトFLUENTを使用した。実用面での利便性が高いFLUENT では、Darcy 則を抵抗の効果として運動方程式に導入している。
【数5】

上記ミクロ解析で求めたデータの近似関数、またはデータマップを用いてマクロ解析を行う。
【0018】
マクロ解析の例として図6 に示す解析条件の問題を考える。横100mm、縦300mm、厚さ0.5mmのマクロ構造体を考える。下面が流入口23,24で、上面が流出口25であり、両側面は壁であると仮定する。入口の中央部20mm幅に水の流入口24がある。水の流入速度は、0.2m/secとする。水の流入口24の両側に各々30mm幅に空気の流入口23が形成されている。空気の流入速度は、0.3m/secとする。流出口25における圧力は、0Paである。
【0019】
ステップ3のマクロ構造の浸透流解析した結果を、図7に示す。また、水12の分布を図8に示す。図8に示した3枚の図は、下から、底面、中間面、上面における水12の存在を示している。濃い部分は、水12が多く存在することを示している。また、空気の分布を図9に示す。図9に示した3枚の図は、下から、底面、中間面、上面における空気の存在を示している。濃い部分は、空気が多く存在することを示している。また、図10に水12及び空気の速度分布を示す。図10に示した3枚の図は、下から、底面、中間面、上面における水及び空気の速度分布を示している。濃い部分は、水及び空気の速度が速いことを示している。
【0020】
以上、詳細に説明したように、本実施例の気液2相流解析方法によれば、多孔体構造体を流れる気液2相の流れをミクロ・マクロスケールで解析する気液2相流解析方法において、想定している立方体ミクロ構造で、3方向圧力勾配及び水飽和度を変化させたときの、浸透係数及び毛管圧力をデータとして記憶し、多孔体構造体の多孔体形状を、データから読み出した浸透係数及び毛管圧力を持った等価均質体に置き換えて、マクロ構造の浸透流解析を行うので、本来の均質化法に基づく非線形マルチスケール解析が、常にミクロスケールの分布性状とマクロスケールの分布性状が平衡状態を保ちながら、マクロスケールの変数を求めるといった非常に大掛かりな解析になるのに対して、本発明の解析はあくまでもマクロ解析のみであり、ミクロスケールの構造を意識する必要はないため、近似である点は精度の劣化が考えられるが、計算コストの面では利便性が高い。ここで、ミクロスケールの構造を意識する必要がないのは、既に浸透係数がミクロスケールの構造を近似したものとして算出されているからである。
【0021】
また、本実施例の気液2相流解析方法によれば、多孔体構造体を流れる気液2相の流れをミクロ・マクロスケールで解析する気液2相流解析方法において、想定している立方体ミクロ構造で、3方向圧力勾配及び水飽和度を変化させたときの、浸透係数及び毛管圧力を関数近似し、その近似された関数を用いてマクロ構造の浸透流解析を行うので、関数近似を用いることで、非連成でマクロ構造及びミクロ構造を解析できるため、ミクロ構造を繰り返すことによる計算コストを必要とせず、計算コストを低減することができる。
すなわち、従来は、ミクロ構造計算した結果を、逐一マクロ構造の浸透流解析にフィードバックしてマクロ構造計算を行い、次のミクロ構造計算を行うという、いわゆる練成計算を行っているため、計算時間が多くかかっていた。それに対して、本実施例では、マクロ解析から、水飽和度Sw、3軸の圧力勾配▽Px、▽Py、▽Pzを用いて、一方的にミクロ構造計算を行い、KαとPcawを関数近似式として求め、その関数近似式を用いて、マクロ構造の浸透流解析を行っているので、逐一ミクロ構造計算を行う必要のない、いわゆる非連成解析アルゴリズムを用いるため、ミクロ解析とマクロ解析とを完全に分離して計算でき、計算時間を短縮することができる。
【0022】
次に、本発明の第2の実施例について説明する。第2の実施例は、第1実施例で得られた図8、9、10の図のうち、詳細なデータを必要とする箇所を図中で指摘することにより、指摘された部分に関して、ミクロ構造体の気液2相流分布を算出するステップを追加したものである。
すなわち、指摘された箇所の立方体ミクロ構造に関して、3軸方向の圧力勾配▽Px、▽Py、▽Pz、及び水飽和度Swを、図8、9、10に示したマクロ構造の浸透流解析結果より求めて、その値を(数1)のミクロ構造支配方程式に代入することにより、ミクロ構造体における水12の分布を得ることができる。得られた分布を図11に示す。想定空間11内で、水12が、分散した状態を示している。濃い色の部分13は、水12が多く存在する部分であり、白色部分15は、水12が存在しない部分であり、薄い色の部分14は、その中間部分である。
【0023】
以上説明したように、第2実施例の気液2相流解析方法によれば、多孔体構造体を流れる気液2相の流れをミクロ・マクロスケールで解析する気液2相流解析方法において、マクロ構造の浸透流解析結果のうち、詳細に評価したい箇所の3方向圧力勾配及びマクロ構造水飽和度を求め、求めた3方向圧力勾配及びマクロ構造水飽和度を立方体ミクロ構造に付与することにより、ミクロ解析を行うので、必要とする箇所について、マクロ構造体の一部のミクロ構造体の気液2相流挙動を把握することができる。
【0024】
このように多孔質体内のミクロ構造を反映したマクロ的な浸透特性を評価した上で,2相浸透流解析を行えば燃料電池の拡散層の水分管理を意図した設計支援が可能となりうる.特に,ミクロ構造内部の幾何性状を設計変数にとることでマクロ特性をコントロールしたり,またマクロ境界条件を変数にとることで飽和度の最適分布を探索する行程の構築するなど燃料電池のCAE における利用価値は高まると考えられる.
【0025】
なお、この発明は前記実施形態に限定されるものではなく、発明の趣旨を逸脱することのない範囲で構成の一部を適宜変更して実施することもできる。
【図面の簡単な説明】
【0026】
【図1】立体ミクロ構造として想定した想定空間11を示す図である。
【図2】水飽和度Swの11のパターンを示す図である。
【図3】気相の透過係数Kaのデータ図である。
【図4】液相の透過係数Kwのデータ図である。
【図5】毛管圧力Pcawのデータ図である。
【図6】マクロ解析の解析条件を示す図である。
【図7】マクロ構造の浸透流解析した結果を示す図である。
【図8】水12の分布を示す図である。
【図9】空気の分布を示す図である。
【図10】水12と空気の速度の分布を示す図である。
【図11】ミクロ構造体における水12の分布を示す図である。
【図12】巨視スケールから微視スケールで気液2相流の流れを模式化した図である。
【符号の説明】
【0027】
11 立方体ミクロ構造
12 水
【特許請求の範囲】
【請求項1】
多孔質体構造体を流れる気液2相の流れをミクロ・マクロスケールで解析する気液2相流解析方法において、
想定している立方体ミクロ構造で、3軸方向圧力勾配、及び水飽和度を変化させたときの、気相浸透係数Ka、液相透過係数Kw、及び毛管圧力Pcawをデータとして記憶し、
前記多孔質体構造体の多孔質体形状を、前記データから読み出した気相浸透係数Ka、液相透過係数Kw、及び毛管圧力Pcawを持った等価均質体に置き換えて、マクロ構造の浸透流解析を行うことを特徴とする気液2相解析方法。
【請求項2】
多孔質体構造体を流れる気液2相の流れをミクロ・マクロスケールで解析する気液2相流解析方法において、
マクロ構造の浸透流解析結果のうち、詳細に評価したい箇所の3軸方向圧力勾配、及びマクロ構造水飽和度を求め、
求めた3軸方向圧力勾配及びマクロ構造水飽和度を立方体ミクロ構造に付与することにより、ミクロ解析を行うことを特徴とする気液2相流解析方法。
【請求項3】
多孔質体構造体を流れる気液2相の流れをミクロ・マクロスケールで解析する気液2相流解析方法において、
想定している立方体ミクロ構造で、3軸方向圧力勾配、及び水飽和度を変化させたときの、気相浸透係数Ka、液相透過係数Kw、及び毛管圧力Pcawを関数近似し、
その近似された関数を用いてマクロ構造の浸透流解析を行うことを特徴とする気液2相流解析方法。
【請求項1】
多孔質体構造体を流れる気液2相の流れをミクロ・マクロスケールで解析する気液2相流解析方法において、
想定している立方体ミクロ構造で、3軸方向圧力勾配、及び水飽和度を変化させたときの、気相浸透係数Ka、液相透過係数Kw、及び毛管圧力Pcawをデータとして記憶し、
前記多孔質体構造体の多孔質体形状を、前記データから読み出した気相浸透係数Ka、液相透過係数Kw、及び毛管圧力Pcawを持った等価均質体に置き換えて、マクロ構造の浸透流解析を行うことを特徴とする気液2相解析方法。
【請求項2】
多孔質体構造体を流れる気液2相の流れをミクロ・マクロスケールで解析する気液2相流解析方法において、
マクロ構造の浸透流解析結果のうち、詳細に評価したい箇所の3軸方向圧力勾配、及びマクロ構造水飽和度を求め、
求めた3軸方向圧力勾配及びマクロ構造水飽和度を立方体ミクロ構造に付与することにより、ミクロ解析を行うことを特徴とする気液2相流解析方法。
【請求項3】
多孔質体構造体を流れる気液2相の流れをミクロ・マクロスケールで解析する気液2相流解析方法において、
想定している立方体ミクロ構造で、3軸方向圧力勾配、及び水飽和度を変化させたときの、気相浸透係数Ka、液相透過係数Kw、及び毛管圧力Pcawを関数近似し、
その近似された関数を用いてマクロ構造の浸透流解析を行うことを特徴とする気液2相流解析方法。
【図1】


【図2】


【図3】


【図4】


【図5】


【図6】


【図7】


【図8】


【図9】


【図10】


【図11】


【図12】




【図2】


【図3】


【図4】


【図5】


【図6】


【図7】


【図8】


【図9】


【図10】


【図11】


【図12】


【公開番号】特開2009−134976(P2009−134976A)
【公開日】平成21年6月18日(2009.6.18)
【国際特許分類】
【出願番号】特願2007−309854(P2007−309854)
【出願日】平成19年11月30日(2007.11.30)
【出願人】(000003207)トヨタ自動車株式会社 (59,920)
【Fターム(参考)】
【公開日】平成21年6月18日(2009.6.18)
【国際特許分類】
【出願日】平成19年11月30日(2007.11.30)
【出願人】(000003207)トヨタ自動車株式会社 (59,920)
【Fターム(参考)】
[ Back to top ]

