製造プロセス変更に起因する変化量の算出方法
【課題】製造プロセスにおいて、それら入口と出口の品質条件の変動の影響を補正し、製造プロセス変更に起因する変化量を精度良く算出する製造プロセス変更に起因する変化量の算出方法を提供すること。
【解決手段】製造工程の変更により製造コストに影響して現われた変化量を、より正確に推定していくため、PLS回帰の手法を用いて、原料性状や、仕上り品質の経時変化などの外乱に影響された変化量の大きさに補正を加えることにより、製造工程変更の影響の大きさを推定する。目的変数に影響する複数の変数を説明変数として、複数の変数間に内在している、信頼性の高い線形の重回帰式の関係を、PLS回帰を用いて見つける。見出された重回帰式は、複数の変数間に内在する関係を線形式で表しているので、その重回帰式で求められてきた説明変数の係数値を利用して、目的変数に補正を加えることにより判定する方法である。
【解決手段】製造工程の変更により製造コストに影響して現われた変化量を、より正確に推定していくため、PLS回帰の手法を用いて、原料性状や、仕上り品質の経時変化などの外乱に影響された変化量の大きさに補正を加えることにより、製造工程変更の影響の大きさを推定する。目的変数に影響する複数の変数を説明変数として、複数の変数間に内在している、信頼性の高い線形の重回帰式の関係を、PLS回帰を用いて見つける。見出された重回帰式は、複数の変数間に内在する関係を線形式で表しているので、その重回帰式で求められてきた説明変数の係数値を利用して、目的変数に補正を加えることにより判定する方法である。
【発明の詳細な説明】
【技術分野】
【0001】
本発明は、PLS回帰法を用いた製造プロセス変更に起因する変化量の算出方法に関する。
【背景技術】
【0002】
製造プロセスに新たに導入された制御システムや、操業方法の変更が、その製造プラントの生産性などに与える影響を数値的に算出しようとする場合、影響の大きさは、通常、データベースに保存された長期間の実機操業での操業データを利用して解析することで算出される。
【0003】
実機操業では、製造工程に入ってくる原料の性状が時間と共に頻繁に変化したり、仕上り品質が許容幅で時間につれて変動したりすることは避けられない。また、製品仕様に伴い製造工程での仕上り品質も変わってくる。そのため、入口と出口の品質条件などが等しい理想的なデータを収集することは困難である。
【0004】
そのため、製造プロセスの変更に起因する変化量の大きさを正確に算定するためには、その製造プラントにおける入口と出口の品質条件などの外乱を製造プロセス変更前後で等しくする補正を加える必要がある。尚、製造プロセス変更の影響が大きく、変化量が大きい場合には、この外乱の影響は相対的に小さくなるので高精度の補正は必ずしも必要としない。
【先行技術文献】
【非特許文献】
【0005】
【非特許文献1】小河守正、加納学、「化学プロセス制御技術者の実践と挑戦」、システム/制御/情報、52巻、8号、2008年
【非特許文献2】宮下芳勝、佐々木慎一、「ケモメトリックス−化学パターン認識と多変量解析」、共立出版、1995年
【非特許文献3】尾崎幸洋、宇田明史、赤井俊雄、「化学者のための多変量解析」、講談社サイエンティフィク、2007年
【発明の概要】
【発明が解決しようとする課題】
【0006】
しかしながら、製造プロセス変更の影響が小さく、その数値の変化量が極小幅である場合には、高い精度で補正を行なって外乱の影響を排除できないと、製造プロセス変更の影響の有無すら判定することが難しくなる。
【0007】
例えば、製造プラントの生産性を向上する目的で化学プラントに良く適用される、高度制御の機能であるモデル予測制御を新たに適用した場合でも、製造工程での省エネルギーや生産性向上で実現される平均的な効果量の実績値は、製造コストの3〜5%ほどの向上幅であったとの調査報告がある(非特許文献1参照)。
【0008】
ここで例えば、紙製造時のクラフトパルプ原料の漂白工程で必要とされる漂白薬品コストが2〜3円/パルプkgほどであるパルプ漂白工程において、高度制御機能の導入により期待される漂白工程での漂白薬品コストの向上効果は、2〜3円/パルプkg×3〜5%≒0.06〜0.15円/パルプkgとなり、ごく小幅の変化と推定される。
【0009】
これに加えて、実際の漂白工程に入ってくるパルプ原料の性状や、仕上り品質などの状態は、時間と共に頻繁に変動し、それら多くの外乱の影響も受けて、漂白薬品コストの値自体も微妙に変動してくる。
【0010】
従来、このような効果量が微少で、かつ、入口と出口の品質条件の変動がある製造プラントにおいて、新たに導入した制御機能や操業方法などの製造プロセス変更に起因する変化量を正確に推定していくことは難しく、場合によっては、解析を諦めその導入又は変更による効果は「不明」として片付けられることも多かった。
【0011】
本発明は、このような課題に鑑みてなされたもので、その目的とするところは、原料の性状や、仕上り品質などが、時間と共に変化してくる製造プロセスにおいて、それら入口と出口の品質条件の変動の影響を補正し、制御機能や操業方法などの製造プロセス変更に起因する変化量を精度良く算出する製造プロセス変更に起因する変化量の算出方法を提供することにある。
【課題を解決するための手段】
【0012】
上記の課題を解決するために、請求項1に記載の発明は、製造プロセス変更に起因する変化量の算出方法であって、製造プロセス変更前後のそれぞれにおいて、前記製造プロセスにおいて各種センサーによって観測された値に基づく変数の内の1つを目的変数とし、他の変数を説明変数として前記説明変数の数以下の数の潜在変数に関してPLS回帰係数を算出するステップと、前記目的変数と所定の前記説明変数とに基づく単回帰式の回帰係数を算出するステップと、所定の前記説明変数の前記PLS回帰係数の正負符号と前記単回帰式の回帰係数の正負符号とが一致する前記潜在変数の数を特定するステップと、前記特定された潜在変数の数において、予測平均二乗誤差を算出し、前記予測平均二乗誤差が適切な潜在変数の数を特定するステップと、前記予測平均二乗誤差が適切と特定された潜在変数の数におけるPLS回帰係数に基づき、製造プロセス変更前後において前記説明変数が同一の値となる場合の前記目的変数をそれぞれ算出して前記目的変数の変化量を算出するステップとを有することを特徴とする。
【0013】
請求項2に記載の発明は、請求項1に記載の製造プロセス変更に起因する変化量の算出方法において、前記説明変数は、前記目的変数に対して相関がある外乱変数であることを特徴とする。
【0014】
請求項3に記載の発明は、請求項1又は2に記載の製造プロセス変更に起因する変化量の算出方法において、前記潜在変数の数を特定するステップは、所定の前記説明変数の前記PLS回帰係数が前記単回帰式の回帰係数から所定の範囲内の大きさである前記潜在変数の数を特定することを特徴とする。
【0015】
請求項4に記載の発明は、請求項1乃至3のいずれかに記載の製造プロセス変更に起因する変化量の算出方法において、前記製造プロセスはパルプ漂白工程であり、前記目的変数は漂白薬品コストであり、前記説明変数は、木材チップの配合率、入りカッパー価、入りパルプ白色度、仕上り原料の白色度から入りパルプ白色度を減算したパルプ白色度の増加幅、最終K価、漂白工程での生産レートであることを特徴とする。
【発明の効果】
【0016】
本発明は、原料の性状や、仕上り品質などが、時間と共に変化してくる製造プロセスにおいて、それら入口と出口の品質条件の変動の影響を補正し、制御効果や性能変化などの製造プロセス変更に起因する変化量を算出する精度を向上させる効果を奏する。
【図面の簡単な説明】
【0017】
【図1】多段の漂白塔で構成される漂白段からなるクラフトパルプの漂白工程のフローを示す図である。
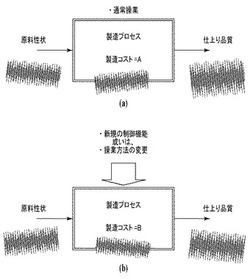
【図2】(a)は製造プロセス変更前の原料性状、製造コスト、仕上り品質を模式的に示す図であり、(b)は製造プロセス変更後の原料性状、製造コスト、仕上り品質を模式的に示す図である。
【図3】生産レートに対する漂白薬品コストの関係を示す図である。
【図4】運転モードが「手動運転」、「漂白制御Aモード」、「漂白制御Bモード」の各場合における、「漂白薬品コスト/パルプkg」を示す図である。
【図5】例示のパルプ原料の漂白工程において、制御機能を使用しない期間データに対して、PLS回帰法を用いた統計解析の結果を示す図である。
【図6】例示のパルプ原料の漂白工程において、制御機能を使用した期間データに対して、PLS回帰法を用いた統計解析の結果を示す図である。
【図7】PLS回帰法での潜在変数の数と予測平均二乗誤差との関係を示す図である。
【図8】MLR回帰法による解析結果について示す図である。
【図9】運転モードが「手動運転」、「漂白制御Aモード」、「漂白制御Bモード」の各場合における、PLS回帰の結果を用いて修正を施した「漂白薬品コスト/パルプkg」を示す図である。
【発明を実施するための形態】
【0018】
以下、本発明の実施の形態について、詳細に説明する。
【0019】
本発明では、製造工程に新たに導入された制御機能や、製造工程での操業方法の変更により、製造コストに影響して現われた真の変化量を、より正確に推定していくため、統計手法の1つであるPLS(Partial Least Squares)回帰の手法を用いて、原料性状や、仕上り品質の経時変化などの外乱に影響された変化量の大きさを、より信頼性の高い形で算定して、製造コスト、例えば、製造原単位の値に補正を加えることにより、影響の大きさを推定する。
【0020】
具体的には、薬品コストを目的変数とし、それに影響する複数の変数を説明変数として、複数の変数間に内在している、信頼性の高い線形の重回帰式の関係を、PLS回帰を用いて見つける。
【0021】
そのようにして見出された重回帰式は、複数の変数間に内在する関係を線形式で表しているので、その重回帰式で求められてきた説明変数の係数値を利用して、最終的に目的変数である薬品コストのデータに補正を加えることにより判定する方法である。
【0022】
従来は、製造コストに対して、適切な補正方法が提案されていなかったため、特に、新たに導入された制御方法や、操業方法の変更などによる製造コストの低減幅が微少量の場合、正しくその影響を判定できず曖昧のまま解析不明として終えることも多かったが、本発明により、影響量について、より精度良く数値化することで合理的に判定していくことが可能となる。
【0023】
目的変数と説明変数間の線型の重回帰式の関係を求める統計手法として、良く使われている最小二乗法を用いた重回帰(MLR:Multiple Linear Regression)手法があるが、本発明では、MLR回帰法の欠点と言われている、「多重共線性」の問題や「過度の当嵌め」の問題を回避することができるPLS(Partial Least Squares)回帰を用いる。
【0024】
これにより、変数間に内在するより信頼性の高い線形の重回帰式の関係を見出すことが可能となり、さらに、そこで得られた重回帰式の係数値を利用することにより、製造コストの値に補正を加え、より精度高く製造コストを推定できるようになる。
【0025】
すなわち、パルプ漂白工程においては、新たに導入された制御機能や操業方法の改善が製造プラントの生産性などに与える影響について、漂白工程に添加して消費された漂白薬品の薬品コストの長期間の変化から解析する場合、PLS回帰法を用いることにより、新たに導入された制御機能や、操業方法の改善に影響されて変化した分と、原料性状や仕上り品質の変化などの外乱に影響されて変化した分の大きさとをより正確に分離して、評価することができる。これにより、製造コストに対する原料性状や仕上り品質の経時変化などの外乱に起因した変化分の大きさを精度高く算定して製造コストの値に高精度の補正を加えることができる。
【0026】
以下、パルプ原料の漂白工程での事例について、具体的な解析方法について説明していく。
【0027】
クラフトパルプ原料の漂白工程は、パルプ製造工程の後方に配置され、複数の漂白薬品を使って、前段のパルプ蒸解工程で作られたパルプ原料を、目標とする白色度になるように多段漂白工程と呼ばれる設備で漂白していく。
【0028】
図1に、多段の漂白塔で構成される漂白段からなるクラフトパルプの漂白工程のフローを示す。各漂白塔において、複数の漂白薬品を、順次、添加してパルプ原料を漂白していく。この漂白工程により、例えば、最初、ISO白色度40%位であった薄茶色のパルプ原料が段階的に漂白されて、最終的に製品管理値が例えばISO白色度85%の高白色度のパルプに漂白されていく。尚、パルプ原料のISO白色度は100%を最大値として、値が大きくなる程、パルプ漂白が進行してパルプ原料の白さが増していく。
【0029】
このパルプ漂白工程では、パルプ原料の漂白処理に使われる高価な漂白薬品のコスト低減化が期待されるが、その場合、日単位で計算され「原単位」とも呼ばれる漂白薬品コスト/パルプkgの日平均値で管理されていることが多い。
【0030】
パルプ漂白工程でパルプ原料に添加して消費された漂白薬品費の1日当りの総額(円/日)は、各漂白薬品の単価(円/L)の値と、その漂白薬品の添加流量を終日集計した積算値(L/日)とを乗算して求め、さらに、パルプ漂白工程で使われた全ての漂白薬品についてそれらを積算することで計算される。また一方、パルプ漂白工程で処理された1日当りのパルプ総重量(Ton/日)は、パルプ漂白工程内に設置された流量計の値を終日集計した積算値(m3/日)とパルプ原料濃度の日平均値(%)、そして、パルプ原料の比重値(通常1.0を使う)から計算される。
【0031】
そして最終的に、上記の終日集計した漂白薬品費の総額(円/日)とパルプ総重量(Ton/日)の2つの値から、パルプ漂白工程で、その日に使われた全漂白薬品の日単位での「漂白薬品コスト値(円/パルプkg)」を計算することができる。
【0032】
そして、計算された値が低い値であるほど、そのパルプ漂白工程において優れた操業が行われたことになり、その日の生産性は高いと判断される。
【0033】
尚、漂白薬品コスト値は、日単位ではなく、分単位や時単位の短周期で計算することもできるが、流量計などのセンサー指示値の変動(ドリフト)誤差に起因する漂白薬品コスト値の計算精度の悪化を回避するため、実際の紙パルプ工場での漂白薬品コストを初めとする「原単位値」では、計算値に高い信頼のおける1日間を通じての積算値を使い、日単位で計算した値で管理するのが一般的である。
【0034】
次に、このパルプ漂白工程の生産性を向上させる目的で、新しい何らかの制御機能をパルプ漂白工程に組み込み、その制御機能による影響(変化量の大きさ)を数値として算出する。
【0035】
その場合、制御機能を使用した期間と使用しなかった期間に対して、日単位のパルプ原料の全漂白薬品コストの値を比較すれば、導入した制御機能の影響の大きさについて判定することができるはずである。しかし、長期間(数か月から年間規模)に渡るプロセスデータから算出された「漂白薬品コスト」の値を基に、単純に比較しようとした場合、原料性状や仕上り品質の変化などの影響のため、導入された制御機能による影響について判定を下しづらいことが多い。その理由として、次の(1)から(6)の六つほどの原因が上げられる。
【0036】
(1)漂白工程の最初の漂白段(漂白塔)に入ってくるパルプ白色度の値は、前工程の状態の関係で、高くなったり低くなったり経時で頻繁に変動することが避けられず、漂白工程に流入してくる白色度の変動が、それ以降の漂白工程での漂白性に直接に影響を与え、漂白薬品コストの値が変化してくる。
【0037】
(2)漂白工程で最終的に完成したパルプ原料の白色度は、使用先の用途に従って、白色度の値が少しずつ異なったものが作られることがあり、最終仕上り白色度の値は変化する。また目標白色度に対して、若干の白色度の差異を生じながら変動することは避けられないし、操業状況によっては、最終白色度の目標値から大きく外してしまうミス操作も時々起こるが、これらの最終白色度の変化や変動が、漂白工程での漂白性に影響を与え、漂白薬品コストの値を変化させる。
【0038】
(3)上述した漂白工程の最初の漂白段(漂白塔)に入ってくるパルプ白色度の変動と同様に、パルプ原料の「カッパー価」の値が、前工程の状態の関係で、高くなったり低くなったり経時で変動することがあり、この「カッパー価」の変動が漂白工程での漂白性に影響を与え、漂白薬品コストの値を変化させる。
【0039】
(4)また、漂白工程の最初の漂白段(漂白塔)に入ってくるパルプ白色度と同様に、漂白工程の最終段(漂白塔)で、最後の漂白処理を終えたパルプ原料の「K価(ケーカと読む)」の値が、漂白工程内での漂白反応状態の関係で、高くなったり低くなったり経時で変動することがあるが、その場合にも、漂白工程内でのパルプ原料の漂白反応に違いが出てくるため、漂白薬品コストの値が変化してくる。
【0040】
補足すれば、パルプの原料となる木材チップは、大まかに、パルプ原料になり得るセルロース成分、ヘミセルロース成分と、パルプ原料として余り適切ではないリグニン成分の三成分で構成されているが、「カッパー価(JIS P 8211:1998にて規定)」と「K価(JIS P 8206:1994にて規定)」は、どちらの値もパルプ原料中にまだ残留しているリグニン成分含量の指標値を表わしており、両値共に、値が大きいほどパルプ原料中にリグニン成分量が多く残っていることになる。
【0041】
尚、漂白工程に入ってくるパルプ原料に対してはリグニン成分量の評価値として「カッパー価」での評価が使われ、漂白処理を終えて漂白工程から出たパルプ原料に対しは「K価」での評価が普通、使われるが、漂白工程を終えたパルプ原料中には漂白反応によりリグニン成分はほとんど分解され、リグニン成分がごく少量しか含まれないため、微少のリグニン成分量も測定できる「K価」の指標での測定法が用いられ、漂白工程に入ってくる「入りカッパー価」の値は大体10近辺の値を取り、漂白工程を終えた「仕上り原料のK価」の値は1近辺の値を取る。
【0042】
(5)漂白工程で漂白処理されるパルプ原料は、漂白工程の前段のパルプ蒸解工程において、木材チップを苛性ソーダと硫化ソーダからなる蒸解薬液を使って、高温高圧下の連続蒸解釜での蒸解反応によって作られるが、パルプ原料として使われる木材チップには、木材材種によって漂白性にかなりの差があり、漂白し易いものと、漂白しづらいものとがある。
【0043】
パルプ蒸解工程では、通常10種類ほどの材種の木材チップの内、在庫のあるものの中から最終製品の諸品質仕様を満足させるように数種類の木材チップを選択、それら複数種類の木材チップを適切な配合率でブレンドした後、蒸解反応によりパルプ原料を製造していくが、使用した木材材種と、その配合率の割合が、ここで対象としている漂白工程でのパルプ原料の漂白性に影響を与えることにより、漂白薬品コストの値が変化してくる。補足すれば、木材チップにはパルプ漂白が容易な易漂白性のものと、パルプ漂白が難しい難漂白性のものとがあるためである。
【0044】
(6)パルプ原料の漂白工程に特有な項目となるが、漂白工程での漂白パルプの生産レート(単位時間当たりの生産量)は、日によって大きく変わることが多いが、パルプ原料の漂白工程では生産レートが高い程、漂白薬品コストの値が悪化することが良く知られている。パルプ原料の漂白反応は漂白工程の漂白塔の内部を通過しながら進行するが、漂白塔の容積は一定であるため、生産レートが高くなるとパルプ原料の漂白塔の内部での滞留時間が短くなり、規定の最終白色度が得られ難くなるため、及び、各漂白塔後のパルプ洗浄用フィルターでの単位生産量当りの洗浄負荷が増え、パルプ洗浄状態が悪化するため、その対応として、漂白薬品の添加量を増添する必要が出てくることが、漂白薬品コストの値が悪化する理由である。
【0045】
以上、述べてきたように、時間と共に、原料性状や仕上り品質が変化するパルプ漂白工程において、導入された制御機能の影響の大きさを正しく判定していくためには、漂白薬品コストの日毎の漂白薬品コスト値の大小で単純に比較するだけでは不十分である。
【0046】
即ち、正しく判定するためには、制御機能自体による影響の大きさについてと、原料性状や仕上り品質の変化から生じて来る上述(1)〜(6)の項目などによる影響の大きさとをきちんと分離、考慮して、原料性状や仕上り品質の経時変化に起因する影響分を差し引いて、漂白薬品コスト値に適切な補正を施して評価する必要がある。
【0047】
このように、パルプ原料の漂白工程の製造プラントは複雑であるが、製造されたパルプ原料の白色度は、上述した(1)〜(6)のように、製造時には、次の外乱の影響を受けていると考えられる。
【0048】
つまり、パルプ原料を作るために使われる複数種類ある木材材種の「(A)木材チップの配合率」、漂白工程に入って来た時のパルプ原料の「(B)入りカッパー価」の値、そして、漂白工程に入って来た時の「(C)入りパルプ白色度」の値、そして、ここでは最終工程を出た「仕上り原料の白色度」ではなく、「仕上り原料の白色度」から「(C)入りパルプ白色度」の値を減算した値である「(D)パルプ白色度の増加幅」が影響を与え、さらに、「(E)仕上り原料の最終K価」の値、そして、「(F)漂白工程での生産レート」に影響を受けているとして解析することにした。
【0049】
尚、「(A)木材チップの配合率」の変数として、ここでは10種類の木材材種の木材チップが存在したので、これだけで10個の変数(A-1)〜(A-10)となり、(A-1)〜(A-10)、(B)、(C)、(D)、(E)、(F)全体で説明変数として使用して行く変数の数は15個となった。また、それら(A-1)〜(A-10)、(B)、(C)、(D)、(E)、(F)の15個の変数の解析に用いたデータは全て、操業を管理している部署が、日単位で算出した1日間の平均値を用い、ここでは、約1年間超に渡る400個ほどのデータ群を使用して行った。
【0050】
尚、最小二乗法を用いた重回帰(MLR:Multiple Linear Regression)により求められる回帰式は、(1)式で表される。「Y」は目的変数、「X」は説明変数(入力変数)で、「a」は各説明変数の回帰係数である。
【0051】
・MLR回帰式
Y=a0+a1・X1+a2・X2+・・・・+an・Xn (1)
MLR回帰では、重回帰式に採用する説明変数の数が多くなってくると、オーバーフィッティングと呼ばれる「過度の当て嵌め現象」が生じ、求まってくる重回帰式の係数値の状態が不適切なものとなってくることがある。
【0052】
対策として、できるだけ少ない説明変数で、適切な回帰式を見つけることが必要となるが、本明細書での問題のように、全ての説明変数を使う必要があることもあるし、採用変数の数を減らすとどうしても回帰式の推定値精度が悪化してくる。
【0053】
それに対し、PLS(Partial Least Squares)回帰では「縮約」と呼ばれる操作によって、「潜在変数」という複数の変数を新たに作り、それらの「潜在変数:T」を用いて回帰式を作成することにより、主成分分析のように、見掛けの説明変数の数を減らすことができる。
【0054】
PLS回帰は(2)式の形で表され、「Y」は目的変数、「X」は説明変数(入力変数)、「T」は潜在変数で、「b」は潜在変数の回帰係数、「w」は潜在変数の各重みである。
【0055】
・PLS回帰式
Y=b0+b1・T1+b2・T2+・・・・・・+br・Tr (2)
但し、第1潜在変数:T1=w11・X1+w12・X2+・・・・+w1n・Xn
第2潜在変数:T2=w21・X1+w22・X2+・・・・+w2n・Xn
・・・・
第r潜在変数:Tr=wr1・X1+wr2・X2+・・・・+wrn・Xn
【0056】
このPLS回帰により説明変数の次元数を減らし、MLR回帰のように、モデル式をデータに、無理矢理、合わせ込んでしまう「過度の当て嵌め現象」を回避したり、説明変数間相互に強い相関性があったり説明変数間に1次従属な関係があったりする場合に、回帰解析で求まってくる係数値が不安定となる「多重共線性」の問題を回避することが可能となる。
【0057】
PLS回帰は、「目的変数」と「潜在変数」間の相関性と、「潜在変数」の分散の両方を同時に考慮し、もともとの入力変数間に存在する非独立性の問題を回避することができる回帰モデルで、「目的変数」と最も強い「潜在変数」を「説明変数」として線形回帰分析を行なう手法で、「主成分分析」と「重回帰分析」の中間的な線形回帰分析法として知られている。
【0058】
PLS回帰では「潜在変数」という変数を用いるが、(2)式の各項について展開操作を行うと、最終的に、(1)式のMLR回帰法と同じ形である判り易い、もともとの説明変数(入力変数)を使った(3)式のような重み付き和で表わされるため、直感的に理解し易い。尚、「Y」は目的変数、「X」は説明変数(入力変数)、「T」は潜在変数で、「b」は潜在変数の回帰係数、「w」は潜在変数の各重みで、「c」は(2)式で求めた潜在変数を展開して現れてきた回帰係数である。
【0059】
・PLS回帰式に、「潜在変数」を代入して展開すると、
Y=b0+b1・T1+b2・T2+・・・+br・Tr
=b0+b1・(w11・X1+w12・X1+・・・+w1n・Xn)
+b2・(w21・X1+w22・X1+・・・+w2n・Xn)
+・・・+br・(wr1・X1+wr2・X1+・・・+wrn・Xn)
=c0+c1・X1+c2・X2+・・・+cn・Xn (3)
【0060】
尚、PLS回帰で作ることができる「潜在変数」の数は、最大元々の説明変数(入力変数)の数まで作ることができる。そして、PLSのアルゴリズムにより最初に計算される「潜在変数」を「第1潜在変数」、そして、「第1潜在変数」を用いたPLS回帰モデルで一致させられなかった残差成分に対して次に計算される「潜在変数」を「第2潜在変数」、以下、同様に「第3潜在変数」、「第4潜在変数」、・・・・と呼び、説明変数(入力変数)の変数の数と同じの全ての「潜在変数」を用いたPLS回帰モデル式は、最小二乗法を用いたMLR重回帰モデル式とほぼ一致する。
【0061】
PLS回帰において、モデル式をデータに無理矢理、合わせ込んでしまう「過度の当て嵌め現象」を回避するためには、PLS回帰式に全ての「潜在変数」を取り込むのではなく、「潜在変数」の数を制限して取り込み、より適切なPLS回帰式を見つけて行くことがポイントとなる。
【0062】
適切な「潜在変数」の取り込み数を見つけるには、
・元々の説明変数(入力変数)に対して計算されてきた(3)式の「c1〜cn」に当たる係数値の±符号の状態やその係数値の大きさが、実情と合っているかどうか
・取り込む「潜在変数」の増加に対する予測値の「平方平均二乗誤差(RMSEP: root mean squared error of prediction)」の減少状態
についてから判断する。
【0063】
そして、適切なPLS回帰式が得られれば、「目的変数」に対する、複数の「説明変数」との線形の関係式が見出されるため、次の操作として、求められたPLS回帰式の各係数値を利用して、各「説明変数」に対して評価を行ないたい値になるよう、全ての「目的変数」のデータに対して線形補正を加えることにより、同一で等しい条件下の値として「目的変数」のデータ値を修正することができる。
【0064】
尚、同一で等しい条件下で製造されたものとして、目的変数の値を評価して行くために、各説明変数に対して採用する値は、例えば、各説明変数の平均値としても良いし、また、評価を希望する任意の値としても良い。
【0065】
例えば、PLS回帰で求まった式が(3)式で、ある変数の全てのデータに対して、同一で等しい条件下で製造されたものとして評価される基準値が「Xi(base)」で、実際の製造時のその変数の値が「Xi」であった時に、「目的変数」のデータを補正するには、PLS回帰式で求まった(3)式の各係数値「c1〜cn」を利用して、下記の(4)式の補正計算を行なえば良い。
【0066】
Y(補正後の値)
=Y(補正前の値)
−{c1・(X1−X1(base))+c2・(X2−X2(base))
+・・・・・・・・+cr・(Xn−Xn(base))} (4)
【0067】
このようにして修正された目的変数のデータを用いることにより、製造プロセスに新たに導入された制御システムや、操業方法の変更が、該製造プラントの生産性などに与える影響について、より正確な数値に基づき、合理的に判定して行くことができるようになる。
【0068】
(実施例1)
ここで、クラフトパルプ原料の漂白工程に導入された制御システムの、製造プラントの生産性などに与える影響について数値的に解析した例について説明する。
【0069】
この例では、「目的変数」として、「漂白薬品コスト」を取り、「説明変数」には前述したように、「(A)木材チップの配合率」、漂白工程に入って来た時のパルプ原料の「(B)入りカッパー価」の値、そして、漂白工程に入って来た時の「(C)入りパルプ白色度」の値、そして、最終工程を出た「仕上り原料の白色度」から「(C)入りパルプ白色度」の値を減算した「(D)パルプ白色度の増加幅」の値、「(E)仕上り原料の最終K価」の値、「(F)漂白工程での生産レート」を取っている。尚、「(A)木材チップの配合率」の変数には10種類の木材チップがあるため、これだけで10変数(A-1)〜(A-10)となり、(A-1)〜(A-10)、(B)、(C)、(D)、(E)、(F)全体での変数の数は15個となった。
【0070】
図3には、日報データから読み取った約400個の操業データ群を使い、横軸に説明変数の中の1つである(F)の「漂白工程での生産レート」を取り、縦軸に目的変数である「漂白薬品コスト」を取ったグラフを示す。
【0071】
グラフ中のプロット点aは制御機能を用いない時のデータ群で、それらのデータに対し最小二乗法を用いて単回帰式を引くと(A)ラインで近似され、プロット点bは制御機能を用いた時のデータ群で、それらデータに対し単回帰式を引くと(B)ラインで近似される。そして、このグラフ図3からも、「漂白工程での生産レート」が増えるに伴ない、「漂白薬品コスト」が増加する傾向が読み取れる。
【0072】
図4に、図3と同じ日報データを使って、制御機能の使用時、不使用時のそれぞれにおける「漂白薬品コスト」の状態をグラフ化したものを示す。図4では、縦軸に「漂白薬品コスト」を取り、横軸に運転モードを取っているが、制御機能の不使用時の運転モードが「手動運転時」であり、制御機能の使用時の運転モードが「漂白A制御モード」と「漂白B制御モード」である。
【0073】
図4からは、制御機能の不使用時(手動運転時)の「漂白薬品コスト」の平均値に対して、「制御Bモード」使用時の「漂白薬品コスト」の平均値を比較すると、差し引き、約0.03円の変化(効果)と読み取れる。
【0074】
しかし、図3からも判るように使用データは、「漂白工程での生産レート」は400トン/日から750トン/日辺りまで大きく変化しており、少なくともこの「漂白工程での生産レート」変動に対する「漂白薬品コスト」への補正を施さないと制御による影響を正しく算定することはできない。また、「(F)漂白工程での生産レート」の他に、説明変数として考えられたその他の変数である、(A-1)〜(A-10)、(B)、(C)、(D)、(E)も加えた全15変数の影響について、同時に考慮して行く必要がある。
【0075】
そこで次に、図5、6に、目的変数の「漂白薬品コスト」に対して、15変数を「説明変数」として使用してPLS回帰式を求めた計算結果を示す。図5の表は、制御機能の不使用時(手動運転時)のデータ群に対するPLS回帰結果を示し、図6の表は制御機能の使用時のデータ群に対するPLS回帰結果を示す。但し、図6は、「制御Aモード」使用時と「制御Bモード」使用時のデータ群をまとめて解析した結果である。
【0076】
そして、いずれのPLS回帰の解析においても、解析対象の説明変数(入力変数)が15個あるため、最大で、第15潜在変数まで計算することができ、その結果を見ることができる。
【0077】
次に、図5、6のPLS回帰結果の最大15個ある潜在変数の計算値の内、いくつまでの潜在変数を選択して、最終的なPLS回帰式として採用していくべきかという問題がある。
【0078】
図7(a)、(b)は、図5、6の表においてPLS回帰で求められた重回帰式に対して、PLS回帰式に取り込む潜在変数の数を横軸に取り、予測平均二乗誤差(RMSEP:root mean squared error of prediction)の値を縦軸に取ったグラフで、この折れ線の減少具合によって、潜在変数の数の増加に伴うPLS回帰式のデータ群への当て嵌まり具合について判断することができる。
【0079】
図5、6の表と、図7のグラフから、潜在変数をいくつまで採用するのが良いか判断していくが、漂白工程においては、「漂白工程での生産レート」の増加に伴って、「漂白薬品コスト」が増加していく関係があるため、PLS回帰式での、「漂白工程での生産レート」の説明変数の係数符号は「+」で計算されて来なければならないし、図3のグラフの近似回帰線の傾きの状態から、その変数の係数値は「+0.0001〜+0.0005」位のオーダーになるべきと考えられる。尚、図5、6の表中には、各説明変数の係数の正負の期待符号(±)を書き込んだが、木材チップ材種に対する説明変数の期待符号については、樹種による漂白し易さ、漂白しづらさ以外に、その産地や生育状態、部位や保管状態などによっても漂白性にかなりの差があり不可知な要素が多く、一律的な判定は難しいため、成り行き扱いとした。
【0080】
そのため本例では、図7(a)のグラフにおいて予測平均二乗誤差(RMSEP)が比較的良好となってくる第9潜在変数まで採用してしまうと、「漂白工程での生産レート」の説明変数の係数符号が「+」ではなく「−」に変わって、「過度の当て嵌め」現象が発生してしまう。また、その他の説明変数の係数についても正負符号の状態、係数の値の大きさについて注意深く見ていくことにより、最終的に、制御機能の不使用時(手動運転時)、制御機能の使用時の両方のPLS回帰結果に対して、ここでは共に、第6潜在変数までを採用することが良いと判断した。
【0081】
尚、参考までに図8に、同一データを用いて一般に良く使われているMLR回帰による解析結果を示すが、制御機能の不使用時(手動運転時)の方の一番上にある「漂白工程での生産レート」の説明変数の係数符号は「−」として計算され不適切となるため、MLR回帰法では重回帰式の解析においては、この時点で解析に行き詰まってしまうことになる。このような不合理な結果は、MLR回帰法によるオーバーフィッティングによる「過度の当て嵌め」に起因する。
【0082】
これに対して、PLS回帰法を用いると、複数ある潜在変数からの採用判断により、MLR回帰法に比べて、重回帰式の作成を、より合理的に行うことができる。
【0083】
上記のように判断して求めたPLS回帰式の15個の説明変数の各係数値の値を用いて、漂白薬品コストの値に対して、制御機能の不使用時(手動運転時)、制御機能の使用時のデータ群に、前述した(4)式を用いて補正を施す。
【0084】
図9に、補正を施した漂白薬品コストの値の結果に対し、図4と同様に制御機能の使用時、不使用時のそれぞれにおける「漂白薬品コスト」を比較した状態を示す。図4と図9のそれぞれにおける制御機能の使用、不使用による漂白薬品コストへの影響の大きさは、おおよそ下表のように変化してくる。
【0085】
【表1】

【0086】
このように、本発明では、従来の算定方法に比べ、プロセス変更に起因する効果量が小さくても、より合理性の高い算定過程に基づき、より正確な効果量を算定することが可能となる。
【技術分野】
【0001】
本発明は、PLS回帰法を用いた製造プロセス変更に起因する変化量の算出方法に関する。
【背景技術】
【0002】
製造プロセスに新たに導入された制御システムや、操業方法の変更が、その製造プラントの生産性などに与える影響を数値的に算出しようとする場合、影響の大きさは、通常、データベースに保存された長期間の実機操業での操業データを利用して解析することで算出される。
【0003】
実機操業では、製造工程に入ってくる原料の性状が時間と共に頻繁に変化したり、仕上り品質が許容幅で時間につれて変動したりすることは避けられない。また、製品仕様に伴い製造工程での仕上り品質も変わってくる。そのため、入口と出口の品質条件などが等しい理想的なデータを収集することは困難である。
【0004】
そのため、製造プロセスの変更に起因する変化量の大きさを正確に算定するためには、その製造プラントにおける入口と出口の品質条件などの外乱を製造プロセス変更前後で等しくする補正を加える必要がある。尚、製造プロセス変更の影響が大きく、変化量が大きい場合には、この外乱の影響は相対的に小さくなるので高精度の補正は必ずしも必要としない。
【先行技術文献】
【非特許文献】
【0005】
【非特許文献1】小河守正、加納学、「化学プロセス制御技術者の実践と挑戦」、システム/制御/情報、52巻、8号、2008年
【非特許文献2】宮下芳勝、佐々木慎一、「ケモメトリックス−化学パターン認識と多変量解析」、共立出版、1995年
【非特許文献3】尾崎幸洋、宇田明史、赤井俊雄、「化学者のための多変量解析」、講談社サイエンティフィク、2007年
【発明の概要】
【発明が解決しようとする課題】
【0006】
しかしながら、製造プロセス変更の影響が小さく、その数値の変化量が極小幅である場合には、高い精度で補正を行なって外乱の影響を排除できないと、製造プロセス変更の影響の有無すら判定することが難しくなる。
【0007】
例えば、製造プラントの生産性を向上する目的で化学プラントに良く適用される、高度制御の機能であるモデル予測制御を新たに適用した場合でも、製造工程での省エネルギーや生産性向上で実現される平均的な効果量の実績値は、製造コストの3〜5%ほどの向上幅であったとの調査報告がある(非特許文献1参照)。
【0008】
ここで例えば、紙製造時のクラフトパルプ原料の漂白工程で必要とされる漂白薬品コストが2〜3円/パルプkgほどであるパルプ漂白工程において、高度制御機能の導入により期待される漂白工程での漂白薬品コストの向上効果は、2〜3円/パルプkg×3〜5%≒0.06〜0.15円/パルプkgとなり、ごく小幅の変化と推定される。
【0009】
これに加えて、実際の漂白工程に入ってくるパルプ原料の性状や、仕上り品質などの状態は、時間と共に頻繁に変動し、それら多くの外乱の影響も受けて、漂白薬品コストの値自体も微妙に変動してくる。
【0010】
従来、このような効果量が微少で、かつ、入口と出口の品質条件の変動がある製造プラントにおいて、新たに導入した制御機能や操業方法などの製造プロセス変更に起因する変化量を正確に推定していくことは難しく、場合によっては、解析を諦めその導入又は変更による効果は「不明」として片付けられることも多かった。
【0011】
本発明は、このような課題に鑑みてなされたもので、その目的とするところは、原料の性状や、仕上り品質などが、時間と共に変化してくる製造プロセスにおいて、それら入口と出口の品質条件の変動の影響を補正し、制御機能や操業方法などの製造プロセス変更に起因する変化量を精度良く算出する製造プロセス変更に起因する変化量の算出方法を提供することにある。
【課題を解決するための手段】
【0012】
上記の課題を解決するために、請求項1に記載の発明は、製造プロセス変更に起因する変化量の算出方法であって、製造プロセス変更前後のそれぞれにおいて、前記製造プロセスにおいて各種センサーによって観測された値に基づく変数の内の1つを目的変数とし、他の変数を説明変数として前記説明変数の数以下の数の潜在変数に関してPLS回帰係数を算出するステップと、前記目的変数と所定の前記説明変数とに基づく単回帰式の回帰係数を算出するステップと、所定の前記説明変数の前記PLS回帰係数の正負符号と前記単回帰式の回帰係数の正負符号とが一致する前記潜在変数の数を特定するステップと、前記特定された潜在変数の数において、予測平均二乗誤差を算出し、前記予測平均二乗誤差が適切な潜在変数の数を特定するステップと、前記予測平均二乗誤差が適切と特定された潜在変数の数におけるPLS回帰係数に基づき、製造プロセス変更前後において前記説明変数が同一の値となる場合の前記目的変数をそれぞれ算出して前記目的変数の変化量を算出するステップとを有することを特徴とする。
【0013】
請求項2に記載の発明は、請求項1に記載の製造プロセス変更に起因する変化量の算出方法において、前記説明変数は、前記目的変数に対して相関がある外乱変数であることを特徴とする。
【0014】
請求項3に記載の発明は、請求項1又は2に記載の製造プロセス変更に起因する変化量の算出方法において、前記潜在変数の数を特定するステップは、所定の前記説明変数の前記PLS回帰係数が前記単回帰式の回帰係数から所定の範囲内の大きさである前記潜在変数の数を特定することを特徴とする。
【0015】
請求項4に記載の発明は、請求項1乃至3のいずれかに記載の製造プロセス変更に起因する変化量の算出方法において、前記製造プロセスはパルプ漂白工程であり、前記目的変数は漂白薬品コストであり、前記説明変数は、木材チップの配合率、入りカッパー価、入りパルプ白色度、仕上り原料の白色度から入りパルプ白色度を減算したパルプ白色度の増加幅、最終K価、漂白工程での生産レートであることを特徴とする。
【発明の効果】
【0016】
本発明は、原料の性状や、仕上り品質などが、時間と共に変化してくる製造プロセスにおいて、それら入口と出口の品質条件の変動の影響を補正し、制御効果や性能変化などの製造プロセス変更に起因する変化量を算出する精度を向上させる効果を奏する。
【図面の簡単な説明】
【0017】
【図1】多段の漂白塔で構成される漂白段からなるクラフトパルプの漂白工程のフローを示す図である。
【図2】(a)は製造プロセス変更前の原料性状、製造コスト、仕上り品質を模式的に示す図であり、(b)は製造プロセス変更後の原料性状、製造コスト、仕上り品質を模式的に示す図である。
【図3】生産レートに対する漂白薬品コストの関係を示す図である。
【図4】運転モードが「手動運転」、「漂白制御Aモード」、「漂白制御Bモード」の各場合における、「漂白薬品コスト/パルプkg」を示す図である。
【図5】例示のパルプ原料の漂白工程において、制御機能を使用しない期間データに対して、PLS回帰法を用いた統計解析の結果を示す図である。
【図6】例示のパルプ原料の漂白工程において、制御機能を使用した期間データに対して、PLS回帰法を用いた統計解析の結果を示す図である。
【図7】PLS回帰法での潜在変数の数と予測平均二乗誤差との関係を示す図である。
【図8】MLR回帰法による解析結果について示す図である。
【図9】運転モードが「手動運転」、「漂白制御Aモード」、「漂白制御Bモード」の各場合における、PLS回帰の結果を用いて修正を施した「漂白薬品コスト/パルプkg」を示す図である。
【発明を実施するための形態】
【0018】
以下、本発明の実施の形態について、詳細に説明する。
【0019】
本発明では、製造工程に新たに導入された制御機能や、製造工程での操業方法の変更により、製造コストに影響して現われた真の変化量を、より正確に推定していくため、統計手法の1つであるPLS(Partial Least Squares)回帰の手法を用いて、原料性状や、仕上り品質の経時変化などの外乱に影響された変化量の大きさを、より信頼性の高い形で算定して、製造コスト、例えば、製造原単位の値に補正を加えることにより、影響の大きさを推定する。
【0020】
具体的には、薬品コストを目的変数とし、それに影響する複数の変数を説明変数として、複数の変数間に内在している、信頼性の高い線形の重回帰式の関係を、PLS回帰を用いて見つける。
【0021】
そのようにして見出された重回帰式は、複数の変数間に内在する関係を線形式で表しているので、その重回帰式で求められてきた説明変数の係数値を利用して、最終的に目的変数である薬品コストのデータに補正を加えることにより判定する方法である。
【0022】
従来は、製造コストに対して、適切な補正方法が提案されていなかったため、特に、新たに導入された制御方法や、操業方法の変更などによる製造コストの低減幅が微少量の場合、正しくその影響を判定できず曖昧のまま解析不明として終えることも多かったが、本発明により、影響量について、より精度良く数値化することで合理的に判定していくことが可能となる。
【0023】
目的変数と説明変数間の線型の重回帰式の関係を求める統計手法として、良く使われている最小二乗法を用いた重回帰(MLR:Multiple Linear Regression)手法があるが、本発明では、MLR回帰法の欠点と言われている、「多重共線性」の問題や「過度の当嵌め」の問題を回避することができるPLS(Partial Least Squares)回帰を用いる。
【0024】
これにより、変数間に内在するより信頼性の高い線形の重回帰式の関係を見出すことが可能となり、さらに、そこで得られた重回帰式の係数値を利用することにより、製造コストの値に補正を加え、より精度高く製造コストを推定できるようになる。
【0025】
すなわち、パルプ漂白工程においては、新たに導入された制御機能や操業方法の改善が製造プラントの生産性などに与える影響について、漂白工程に添加して消費された漂白薬品の薬品コストの長期間の変化から解析する場合、PLS回帰法を用いることにより、新たに導入された制御機能や、操業方法の改善に影響されて変化した分と、原料性状や仕上り品質の変化などの外乱に影響されて変化した分の大きさとをより正確に分離して、評価することができる。これにより、製造コストに対する原料性状や仕上り品質の経時変化などの外乱に起因した変化分の大きさを精度高く算定して製造コストの値に高精度の補正を加えることができる。
【0026】
以下、パルプ原料の漂白工程での事例について、具体的な解析方法について説明していく。
【0027】
クラフトパルプ原料の漂白工程は、パルプ製造工程の後方に配置され、複数の漂白薬品を使って、前段のパルプ蒸解工程で作られたパルプ原料を、目標とする白色度になるように多段漂白工程と呼ばれる設備で漂白していく。
【0028】
図1に、多段の漂白塔で構成される漂白段からなるクラフトパルプの漂白工程のフローを示す。各漂白塔において、複数の漂白薬品を、順次、添加してパルプ原料を漂白していく。この漂白工程により、例えば、最初、ISO白色度40%位であった薄茶色のパルプ原料が段階的に漂白されて、最終的に製品管理値が例えばISO白色度85%の高白色度のパルプに漂白されていく。尚、パルプ原料のISO白色度は100%を最大値として、値が大きくなる程、パルプ漂白が進行してパルプ原料の白さが増していく。
【0029】
このパルプ漂白工程では、パルプ原料の漂白処理に使われる高価な漂白薬品のコスト低減化が期待されるが、その場合、日単位で計算され「原単位」とも呼ばれる漂白薬品コスト/パルプkgの日平均値で管理されていることが多い。
【0030】
パルプ漂白工程でパルプ原料に添加して消費された漂白薬品費の1日当りの総額(円/日)は、各漂白薬品の単価(円/L)の値と、その漂白薬品の添加流量を終日集計した積算値(L/日)とを乗算して求め、さらに、パルプ漂白工程で使われた全ての漂白薬品についてそれらを積算することで計算される。また一方、パルプ漂白工程で処理された1日当りのパルプ総重量(Ton/日)は、パルプ漂白工程内に設置された流量計の値を終日集計した積算値(m3/日)とパルプ原料濃度の日平均値(%)、そして、パルプ原料の比重値(通常1.0を使う)から計算される。
【0031】
そして最終的に、上記の終日集計した漂白薬品費の総額(円/日)とパルプ総重量(Ton/日)の2つの値から、パルプ漂白工程で、その日に使われた全漂白薬品の日単位での「漂白薬品コスト値(円/パルプkg)」を計算することができる。
【0032】
そして、計算された値が低い値であるほど、そのパルプ漂白工程において優れた操業が行われたことになり、その日の生産性は高いと判断される。
【0033】
尚、漂白薬品コスト値は、日単位ではなく、分単位や時単位の短周期で計算することもできるが、流量計などのセンサー指示値の変動(ドリフト)誤差に起因する漂白薬品コスト値の計算精度の悪化を回避するため、実際の紙パルプ工場での漂白薬品コストを初めとする「原単位値」では、計算値に高い信頼のおける1日間を通じての積算値を使い、日単位で計算した値で管理するのが一般的である。
【0034】
次に、このパルプ漂白工程の生産性を向上させる目的で、新しい何らかの制御機能をパルプ漂白工程に組み込み、その制御機能による影響(変化量の大きさ)を数値として算出する。
【0035】
その場合、制御機能を使用した期間と使用しなかった期間に対して、日単位のパルプ原料の全漂白薬品コストの値を比較すれば、導入した制御機能の影響の大きさについて判定することができるはずである。しかし、長期間(数か月から年間規模)に渡るプロセスデータから算出された「漂白薬品コスト」の値を基に、単純に比較しようとした場合、原料性状や仕上り品質の変化などの影響のため、導入された制御機能による影響について判定を下しづらいことが多い。その理由として、次の(1)から(6)の六つほどの原因が上げられる。
【0036】
(1)漂白工程の最初の漂白段(漂白塔)に入ってくるパルプ白色度の値は、前工程の状態の関係で、高くなったり低くなったり経時で頻繁に変動することが避けられず、漂白工程に流入してくる白色度の変動が、それ以降の漂白工程での漂白性に直接に影響を与え、漂白薬品コストの値が変化してくる。
【0037】
(2)漂白工程で最終的に完成したパルプ原料の白色度は、使用先の用途に従って、白色度の値が少しずつ異なったものが作られることがあり、最終仕上り白色度の値は変化する。また目標白色度に対して、若干の白色度の差異を生じながら変動することは避けられないし、操業状況によっては、最終白色度の目標値から大きく外してしまうミス操作も時々起こるが、これらの最終白色度の変化や変動が、漂白工程での漂白性に影響を与え、漂白薬品コストの値を変化させる。
【0038】
(3)上述した漂白工程の最初の漂白段(漂白塔)に入ってくるパルプ白色度の変動と同様に、パルプ原料の「カッパー価」の値が、前工程の状態の関係で、高くなったり低くなったり経時で変動することがあり、この「カッパー価」の変動が漂白工程での漂白性に影響を与え、漂白薬品コストの値を変化させる。
【0039】
(4)また、漂白工程の最初の漂白段(漂白塔)に入ってくるパルプ白色度と同様に、漂白工程の最終段(漂白塔)で、最後の漂白処理を終えたパルプ原料の「K価(ケーカと読む)」の値が、漂白工程内での漂白反応状態の関係で、高くなったり低くなったり経時で変動することがあるが、その場合にも、漂白工程内でのパルプ原料の漂白反応に違いが出てくるため、漂白薬品コストの値が変化してくる。
【0040】
補足すれば、パルプの原料となる木材チップは、大まかに、パルプ原料になり得るセルロース成分、ヘミセルロース成分と、パルプ原料として余り適切ではないリグニン成分の三成分で構成されているが、「カッパー価(JIS P 8211:1998にて規定)」と「K価(JIS P 8206:1994にて規定)」は、どちらの値もパルプ原料中にまだ残留しているリグニン成分含量の指標値を表わしており、両値共に、値が大きいほどパルプ原料中にリグニン成分量が多く残っていることになる。
【0041】
尚、漂白工程に入ってくるパルプ原料に対してはリグニン成分量の評価値として「カッパー価」での評価が使われ、漂白処理を終えて漂白工程から出たパルプ原料に対しは「K価」での評価が普通、使われるが、漂白工程を終えたパルプ原料中には漂白反応によりリグニン成分はほとんど分解され、リグニン成分がごく少量しか含まれないため、微少のリグニン成分量も測定できる「K価」の指標での測定法が用いられ、漂白工程に入ってくる「入りカッパー価」の値は大体10近辺の値を取り、漂白工程を終えた「仕上り原料のK価」の値は1近辺の値を取る。
【0042】
(5)漂白工程で漂白処理されるパルプ原料は、漂白工程の前段のパルプ蒸解工程において、木材チップを苛性ソーダと硫化ソーダからなる蒸解薬液を使って、高温高圧下の連続蒸解釜での蒸解反応によって作られるが、パルプ原料として使われる木材チップには、木材材種によって漂白性にかなりの差があり、漂白し易いものと、漂白しづらいものとがある。
【0043】
パルプ蒸解工程では、通常10種類ほどの材種の木材チップの内、在庫のあるものの中から最終製品の諸品質仕様を満足させるように数種類の木材チップを選択、それら複数種類の木材チップを適切な配合率でブレンドした後、蒸解反応によりパルプ原料を製造していくが、使用した木材材種と、その配合率の割合が、ここで対象としている漂白工程でのパルプ原料の漂白性に影響を与えることにより、漂白薬品コストの値が変化してくる。補足すれば、木材チップにはパルプ漂白が容易な易漂白性のものと、パルプ漂白が難しい難漂白性のものとがあるためである。
【0044】
(6)パルプ原料の漂白工程に特有な項目となるが、漂白工程での漂白パルプの生産レート(単位時間当たりの生産量)は、日によって大きく変わることが多いが、パルプ原料の漂白工程では生産レートが高い程、漂白薬品コストの値が悪化することが良く知られている。パルプ原料の漂白反応は漂白工程の漂白塔の内部を通過しながら進行するが、漂白塔の容積は一定であるため、生産レートが高くなるとパルプ原料の漂白塔の内部での滞留時間が短くなり、規定の最終白色度が得られ難くなるため、及び、各漂白塔後のパルプ洗浄用フィルターでの単位生産量当りの洗浄負荷が増え、パルプ洗浄状態が悪化するため、その対応として、漂白薬品の添加量を増添する必要が出てくることが、漂白薬品コストの値が悪化する理由である。
【0045】
以上、述べてきたように、時間と共に、原料性状や仕上り品質が変化するパルプ漂白工程において、導入された制御機能の影響の大きさを正しく判定していくためには、漂白薬品コストの日毎の漂白薬品コスト値の大小で単純に比較するだけでは不十分である。
【0046】
即ち、正しく判定するためには、制御機能自体による影響の大きさについてと、原料性状や仕上り品質の変化から生じて来る上述(1)〜(6)の項目などによる影響の大きさとをきちんと分離、考慮して、原料性状や仕上り品質の経時変化に起因する影響分を差し引いて、漂白薬品コスト値に適切な補正を施して評価する必要がある。
【0047】
このように、パルプ原料の漂白工程の製造プラントは複雑であるが、製造されたパルプ原料の白色度は、上述した(1)〜(6)のように、製造時には、次の外乱の影響を受けていると考えられる。
【0048】
つまり、パルプ原料を作るために使われる複数種類ある木材材種の「(A)木材チップの配合率」、漂白工程に入って来た時のパルプ原料の「(B)入りカッパー価」の値、そして、漂白工程に入って来た時の「(C)入りパルプ白色度」の値、そして、ここでは最終工程を出た「仕上り原料の白色度」ではなく、「仕上り原料の白色度」から「(C)入りパルプ白色度」の値を減算した値である「(D)パルプ白色度の増加幅」が影響を与え、さらに、「(E)仕上り原料の最終K価」の値、そして、「(F)漂白工程での生産レート」に影響を受けているとして解析することにした。
【0049】
尚、「(A)木材チップの配合率」の変数として、ここでは10種類の木材材種の木材チップが存在したので、これだけで10個の変数(A-1)〜(A-10)となり、(A-1)〜(A-10)、(B)、(C)、(D)、(E)、(F)全体で説明変数として使用して行く変数の数は15個となった。また、それら(A-1)〜(A-10)、(B)、(C)、(D)、(E)、(F)の15個の変数の解析に用いたデータは全て、操業を管理している部署が、日単位で算出した1日間の平均値を用い、ここでは、約1年間超に渡る400個ほどのデータ群を使用して行った。
【0050】
尚、最小二乗法を用いた重回帰(MLR:Multiple Linear Regression)により求められる回帰式は、(1)式で表される。「Y」は目的変数、「X」は説明変数(入力変数)で、「a」は各説明変数の回帰係数である。
【0051】
・MLR回帰式
Y=a0+a1・X1+a2・X2+・・・・+an・Xn (1)
MLR回帰では、重回帰式に採用する説明変数の数が多くなってくると、オーバーフィッティングと呼ばれる「過度の当て嵌め現象」が生じ、求まってくる重回帰式の係数値の状態が不適切なものとなってくることがある。
【0052】
対策として、できるだけ少ない説明変数で、適切な回帰式を見つけることが必要となるが、本明細書での問題のように、全ての説明変数を使う必要があることもあるし、採用変数の数を減らすとどうしても回帰式の推定値精度が悪化してくる。
【0053】
それに対し、PLS(Partial Least Squares)回帰では「縮約」と呼ばれる操作によって、「潜在変数」という複数の変数を新たに作り、それらの「潜在変数:T」を用いて回帰式を作成することにより、主成分分析のように、見掛けの説明変数の数を減らすことができる。
【0054】
PLS回帰は(2)式の形で表され、「Y」は目的変数、「X」は説明変数(入力変数)、「T」は潜在変数で、「b」は潜在変数の回帰係数、「w」は潜在変数の各重みである。
【0055】
・PLS回帰式
Y=b0+b1・T1+b2・T2+・・・・・・+br・Tr (2)
但し、第1潜在変数:T1=w11・X1+w12・X2+・・・・+w1n・Xn
第2潜在変数:T2=w21・X1+w22・X2+・・・・+w2n・Xn
・・・・
第r潜在変数:Tr=wr1・X1+wr2・X2+・・・・+wrn・Xn
【0056】
このPLS回帰により説明変数の次元数を減らし、MLR回帰のように、モデル式をデータに、無理矢理、合わせ込んでしまう「過度の当て嵌め現象」を回避したり、説明変数間相互に強い相関性があったり説明変数間に1次従属な関係があったりする場合に、回帰解析で求まってくる係数値が不安定となる「多重共線性」の問題を回避することが可能となる。
【0057】
PLS回帰は、「目的変数」と「潜在変数」間の相関性と、「潜在変数」の分散の両方を同時に考慮し、もともとの入力変数間に存在する非独立性の問題を回避することができる回帰モデルで、「目的変数」と最も強い「潜在変数」を「説明変数」として線形回帰分析を行なう手法で、「主成分分析」と「重回帰分析」の中間的な線形回帰分析法として知られている。
【0058】
PLS回帰では「潜在変数」という変数を用いるが、(2)式の各項について展開操作を行うと、最終的に、(1)式のMLR回帰法と同じ形である判り易い、もともとの説明変数(入力変数)を使った(3)式のような重み付き和で表わされるため、直感的に理解し易い。尚、「Y」は目的変数、「X」は説明変数(入力変数)、「T」は潜在変数で、「b」は潜在変数の回帰係数、「w」は潜在変数の各重みで、「c」は(2)式で求めた潜在変数を展開して現れてきた回帰係数である。
【0059】
・PLS回帰式に、「潜在変数」を代入して展開すると、
Y=b0+b1・T1+b2・T2+・・・+br・Tr
=b0+b1・(w11・X1+w12・X1+・・・+w1n・Xn)
+b2・(w21・X1+w22・X1+・・・+w2n・Xn)
+・・・+br・(wr1・X1+wr2・X1+・・・+wrn・Xn)
=c0+c1・X1+c2・X2+・・・+cn・Xn (3)
【0060】
尚、PLS回帰で作ることができる「潜在変数」の数は、最大元々の説明変数(入力変数)の数まで作ることができる。そして、PLSのアルゴリズムにより最初に計算される「潜在変数」を「第1潜在変数」、そして、「第1潜在変数」を用いたPLS回帰モデルで一致させられなかった残差成分に対して次に計算される「潜在変数」を「第2潜在変数」、以下、同様に「第3潜在変数」、「第4潜在変数」、・・・・と呼び、説明変数(入力変数)の変数の数と同じの全ての「潜在変数」を用いたPLS回帰モデル式は、最小二乗法を用いたMLR重回帰モデル式とほぼ一致する。
【0061】
PLS回帰において、モデル式をデータに無理矢理、合わせ込んでしまう「過度の当て嵌め現象」を回避するためには、PLS回帰式に全ての「潜在変数」を取り込むのではなく、「潜在変数」の数を制限して取り込み、より適切なPLS回帰式を見つけて行くことがポイントとなる。
【0062】
適切な「潜在変数」の取り込み数を見つけるには、
・元々の説明変数(入力変数)に対して計算されてきた(3)式の「c1〜cn」に当たる係数値の±符号の状態やその係数値の大きさが、実情と合っているかどうか
・取り込む「潜在変数」の増加に対する予測値の「平方平均二乗誤差(RMSEP: root mean squared error of prediction)」の減少状態
についてから判断する。
【0063】
そして、適切なPLS回帰式が得られれば、「目的変数」に対する、複数の「説明変数」との線形の関係式が見出されるため、次の操作として、求められたPLS回帰式の各係数値を利用して、各「説明変数」に対して評価を行ないたい値になるよう、全ての「目的変数」のデータに対して線形補正を加えることにより、同一で等しい条件下の値として「目的変数」のデータ値を修正することができる。
【0064】
尚、同一で等しい条件下で製造されたものとして、目的変数の値を評価して行くために、各説明変数に対して採用する値は、例えば、各説明変数の平均値としても良いし、また、評価を希望する任意の値としても良い。
【0065】
例えば、PLS回帰で求まった式が(3)式で、ある変数の全てのデータに対して、同一で等しい条件下で製造されたものとして評価される基準値が「Xi(base)」で、実際の製造時のその変数の値が「Xi」であった時に、「目的変数」のデータを補正するには、PLS回帰式で求まった(3)式の各係数値「c1〜cn」を利用して、下記の(4)式の補正計算を行なえば良い。
【0066】
Y(補正後の値)
=Y(補正前の値)
−{c1・(X1−X1(base))+c2・(X2−X2(base))
+・・・・・・・・+cr・(Xn−Xn(base))} (4)
【0067】
このようにして修正された目的変数のデータを用いることにより、製造プロセスに新たに導入された制御システムや、操業方法の変更が、該製造プラントの生産性などに与える影響について、より正確な数値に基づき、合理的に判定して行くことができるようになる。
【0068】
(実施例1)
ここで、クラフトパルプ原料の漂白工程に導入された制御システムの、製造プラントの生産性などに与える影響について数値的に解析した例について説明する。
【0069】
この例では、「目的変数」として、「漂白薬品コスト」を取り、「説明変数」には前述したように、「(A)木材チップの配合率」、漂白工程に入って来た時のパルプ原料の「(B)入りカッパー価」の値、そして、漂白工程に入って来た時の「(C)入りパルプ白色度」の値、そして、最終工程を出た「仕上り原料の白色度」から「(C)入りパルプ白色度」の値を減算した「(D)パルプ白色度の増加幅」の値、「(E)仕上り原料の最終K価」の値、「(F)漂白工程での生産レート」を取っている。尚、「(A)木材チップの配合率」の変数には10種類の木材チップがあるため、これだけで10変数(A-1)〜(A-10)となり、(A-1)〜(A-10)、(B)、(C)、(D)、(E)、(F)全体での変数の数は15個となった。
【0070】
図3には、日報データから読み取った約400個の操業データ群を使い、横軸に説明変数の中の1つである(F)の「漂白工程での生産レート」を取り、縦軸に目的変数である「漂白薬品コスト」を取ったグラフを示す。
【0071】
グラフ中のプロット点aは制御機能を用いない時のデータ群で、それらのデータに対し最小二乗法を用いて単回帰式を引くと(A)ラインで近似され、プロット点bは制御機能を用いた時のデータ群で、それらデータに対し単回帰式を引くと(B)ラインで近似される。そして、このグラフ図3からも、「漂白工程での生産レート」が増えるに伴ない、「漂白薬品コスト」が増加する傾向が読み取れる。
【0072】
図4に、図3と同じ日報データを使って、制御機能の使用時、不使用時のそれぞれにおける「漂白薬品コスト」の状態をグラフ化したものを示す。図4では、縦軸に「漂白薬品コスト」を取り、横軸に運転モードを取っているが、制御機能の不使用時の運転モードが「手動運転時」であり、制御機能の使用時の運転モードが「漂白A制御モード」と「漂白B制御モード」である。
【0073】
図4からは、制御機能の不使用時(手動運転時)の「漂白薬品コスト」の平均値に対して、「制御Bモード」使用時の「漂白薬品コスト」の平均値を比較すると、差し引き、約0.03円の変化(効果)と読み取れる。
【0074】
しかし、図3からも判るように使用データは、「漂白工程での生産レート」は400トン/日から750トン/日辺りまで大きく変化しており、少なくともこの「漂白工程での生産レート」変動に対する「漂白薬品コスト」への補正を施さないと制御による影響を正しく算定することはできない。また、「(F)漂白工程での生産レート」の他に、説明変数として考えられたその他の変数である、(A-1)〜(A-10)、(B)、(C)、(D)、(E)も加えた全15変数の影響について、同時に考慮して行く必要がある。
【0075】
そこで次に、図5、6に、目的変数の「漂白薬品コスト」に対して、15変数を「説明変数」として使用してPLS回帰式を求めた計算結果を示す。図5の表は、制御機能の不使用時(手動運転時)のデータ群に対するPLS回帰結果を示し、図6の表は制御機能の使用時のデータ群に対するPLS回帰結果を示す。但し、図6は、「制御Aモード」使用時と「制御Bモード」使用時のデータ群をまとめて解析した結果である。
【0076】
そして、いずれのPLS回帰の解析においても、解析対象の説明変数(入力変数)が15個あるため、最大で、第15潜在変数まで計算することができ、その結果を見ることができる。
【0077】
次に、図5、6のPLS回帰結果の最大15個ある潜在変数の計算値の内、いくつまでの潜在変数を選択して、最終的なPLS回帰式として採用していくべきかという問題がある。
【0078】
図7(a)、(b)は、図5、6の表においてPLS回帰で求められた重回帰式に対して、PLS回帰式に取り込む潜在変数の数を横軸に取り、予測平均二乗誤差(RMSEP:root mean squared error of prediction)の値を縦軸に取ったグラフで、この折れ線の減少具合によって、潜在変数の数の増加に伴うPLS回帰式のデータ群への当て嵌まり具合について判断することができる。
【0079】
図5、6の表と、図7のグラフから、潜在変数をいくつまで採用するのが良いか判断していくが、漂白工程においては、「漂白工程での生産レート」の増加に伴って、「漂白薬品コスト」が増加していく関係があるため、PLS回帰式での、「漂白工程での生産レート」の説明変数の係数符号は「+」で計算されて来なければならないし、図3のグラフの近似回帰線の傾きの状態から、その変数の係数値は「+0.0001〜+0.0005」位のオーダーになるべきと考えられる。尚、図5、6の表中には、各説明変数の係数の正負の期待符号(±)を書き込んだが、木材チップ材種に対する説明変数の期待符号については、樹種による漂白し易さ、漂白しづらさ以外に、その産地や生育状態、部位や保管状態などによっても漂白性にかなりの差があり不可知な要素が多く、一律的な判定は難しいため、成り行き扱いとした。
【0080】
そのため本例では、図7(a)のグラフにおいて予測平均二乗誤差(RMSEP)が比較的良好となってくる第9潜在変数まで採用してしまうと、「漂白工程での生産レート」の説明変数の係数符号が「+」ではなく「−」に変わって、「過度の当て嵌め」現象が発生してしまう。また、その他の説明変数の係数についても正負符号の状態、係数の値の大きさについて注意深く見ていくことにより、最終的に、制御機能の不使用時(手動運転時)、制御機能の使用時の両方のPLS回帰結果に対して、ここでは共に、第6潜在変数までを採用することが良いと判断した。
【0081】
尚、参考までに図8に、同一データを用いて一般に良く使われているMLR回帰による解析結果を示すが、制御機能の不使用時(手動運転時)の方の一番上にある「漂白工程での生産レート」の説明変数の係数符号は「−」として計算され不適切となるため、MLR回帰法では重回帰式の解析においては、この時点で解析に行き詰まってしまうことになる。このような不合理な結果は、MLR回帰法によるオーバーフィッティングによる「過度の当て嵌め」に起因する。
【0082】
これに対して、PLS回帰法を用いると、複数ある潜在変数からの採用判断により、MLR回帰法に比べて、重回帰式の作成を、より合理的に行うことができる。
【0083】
上記のように判断して求めたPLS回帰式の15個の説明変数の各係数値の値を用いて、漂白薬品コストの値に対して、制御機能の不使用時(手動運転時)、制御機能の使用時のデータ群に、前述した(4)式を用いて補正を施す。
【0084】
図9に、補正を施した漂白薬品コストの値の結果に対し、図4と同様に制御機能の使用時、不使用時のそれぞれにおける「漂白薬品コスト」を比較した状態を示す。図4と図9のそれぞれにおける制御機能の使用、不使用による漂白薬品コストへの影響の大きさは、おおよそ下表のように変化してくる。
【0085】
【表1】

【0086】
このように、本発明では、従来の算定方法に比べ、プロセス変更に起因する効果量が小さくても、より合理性の高い算定過程に基づき、より正確な効果量を算定することが可能となる。
【特許請求の範囲】
【請求項1】
製造プロセス変更前後のそれぞれにおいて、前記製造プロセスにおいて各種センサーによって観測された値に基づく変数の内の1つを目的変数とし、他の変数を説明変数として前記説明変数の数以下の数の潜在変数に関してPLS回帰係数を算出するステップと、
前記目的変数と所定の前記説明変数とに基づく単回帰式の回帰係数を算出するステップと、
所定の前記説明変数の前記PLS回帰係数の正負符号と前記単回帰式の回帰係数の正負符号とが一致する前記潜在変数の数を特定するステップと、
前記特定された潜在変数の数において、予測平均二乗誤差を算出し、前記予測平均二乗誤差が適切な潜在変数の数を特定するステップと、
前記予測平均二乗誤差が適切と特定された潜在変数の数におけるPLS回帰係数に基づき、製造プロセス変更前後において前記説明変数が同一の値となる場合の前記目的変数をそれぞれ算出して前記目的変数の変化量を算出するステップと
を有することを特徴とする製造プロセス変更に起因する変化量の算出方法。
【請求項2】
前記説明変数は、前記目的変数に対して相関がある外乱変数であることを特徴とする請求項1に記載の製造プロセス変更に起因する変化量の算出方法。
【請求項3】
前記潜在変数の数を特定するステップは、所定の前記説明変数の前記PLS回帰係数が前記単回帰式の回帰係数から所定の範囲内の大きさである前記潜在変数の数を特定することを特徴とする請求項1又は2に記載の製造プロセス変更に起因する変化量の算出方法。
【請求項4】
前記製造プロセスはパルプ漂白工程であり、前記目的変数は漂白薬品コストであり、前記説明変数は、木材チップの配合率、入りカッパー価、入りパルプ白色度、仕上り原料の白色度から入りパルプ白色度を減算したパルプ白色度の増加幅、最終K価、漂白工程での生産レートであることを特徴とする請求項1乃至3のいずれかに記載の製造プロセス変更に起因する変化量の算出方法。
【請求項1】
製造プロセス変更前後のそれぞれにおいて、前記製造プロセスにおいて各種センサーによって観測された値に基づく変数の内の1つを目的変数とし、他の変数を説明変数として前記説明変数の数以下の数の潜在変数に関してPLS回帰係数を算出するステップと、
前記目的変数と所定の前記説明変数とに基づく単回帰式の回帰係数を算出するステップと、
所定の前記説明変数の前記PLS回帰係数の正負符号と前記単回帰式の回帰係数の正負符号とが一致する前記潜在変数の数を特定するステップと、
前記特定された潜在変数の数において、予測平均二乗誤差を算出し、前記予測平均二乗誤差が適切な潜在変数の数を特定するステップと、
前記予測平均二乗誤差が適切と特定された潜在変数の数におけるPLS回帰係数に基づき、製造プロセス変更前後において前記説明変数が同一の値となる場合の前記目的変数をそれぞれ算出して前記目的変数の変化量を算出するステップと
を有することを特徴とする製造プロセス変更に起因する変化量の算出方法。
【請求項2】
前記説明変数は、前記目的変数に対して相関がある外乱変数であることを特徴とする請求項1に記載の製造プロセス変更に起因する変化量の算出方法。
【請求項3】
前記潜在変数の数を特定するステップは、所定の前記説明変数の前記PLS回帰係数が前記単回帰式の回帰係数から所定の範囲内の大きさである前記潜在変数の数を特定することを特徴とする請求項1又は2に記載の製造プロセス変更に起因する変化量の算出方法。
【請求項4】
前記製造プロセスはパルプ漂白工程であり、前記目的変数は漂白薬品コストであり、前記説明変数は、木材チップの配合率、入りカッパー価、入りパルプ白色度、仕上り原料の白色度から入りパルプ白色度を減算したパルプ白色度の増加幅、最終K価、漂白工程での生産レートであることを特徴とする請求項1乃至3のいずれかに記載の製造プロセス変更に起因する変化量の算出方法。
【図1】


【図2】


【図3】


【図4】


【図5】


【図6】


【図7】


【図8】


【図9】




【図2】


【図3】


【図4】


【図5】


【図6】


【図7】


【図8】


【図9】


【公開番号】特開2013−105313(P2013−105313A)
【公開日】平成25年5月30日(2013.5.30)
【国際特許分類】
【出願番号】特願2011−248615(P2011−248615)
【出願日】平成23年11月14日(2011.11.14)
【出願人】(000122298)王子ホールディングス株式会社 (2,055)
【出願人】(000191320)王子エフテックス株式会社 (79)
【Fターム(参考)】
【公開日】平成25年5月30日(2013.5.30)
【国際特許分類】
【出願日】平成23年11月14日(2011.11.14)
【出願人】(000122298)王子ホールディングス株式会社 (2,055)
【出願人】(000191320)王子エフテックス株式会社 (79)
【Fターム(参考)】
[ Back to top ]

