軌道計画方法、軌道計画システム及び軌道計画・制御システム
【課題】運動コストを最小化するように状態空間を分割し、より精度よく準コスト最小軌道を計画することのできる軌道計画方法を提供する
【解決手段】本発明による軌道計画方法は、軌道計画システム(100)によって物体の状態を目標状態へ制御するための軌道を求める軌道計画方法であって、該物体の状態空間をセルに分割するセル作成部(103)が、所定のセルの数に対して、離散化による近似誤差を最小化するように該状態空間をセルに分割するステップと、探索木作成部(101)が、該状態空間において、該物体の状態遷移に対応する探索木を、該物体の状態に対応する、該探索木の枝のノードがセルに一つずつ含まれるように作成するステップと、軌道作成部(107)が、該探索木を使用して、該物体の現在の状態から目標状態までの経路を定めるステップと、を含む。
【解決手段】本発明による軌道計画方法は、軌道計画システム(100)によって物体の状態を目標状態へ制御するための軌道を求める軌道計画方法であって、該物体の状態空間をセルに分割するセル作成部(103)が、所定のセルの数に対して、離散化による近似誤差を最小化するように該状態空間をセルに分割するステップと、探索木作成部(101)が、該状態空間において、該物体の状態遷移に対応する探索木を、該物体の状態に対応する、該探索木の枝のノードがセルに一つずつ含まれるように作成するステップと、軌道作成部(107)が、該探索木を使用して、該物体の現在の状態から目標状態までの経路を定めるステップと、を含む。
【発明の詳細な説明】
【技術分野】
【0001】
本発明は、物体の、目標状態に至る状態遷移系列を作成する、軌道計画方法、軌道計画システム及び上記軌道計画システムを備えた軌道計画・制御システムに関する。
【背景技術】
【0002】
たとえば、ロボットのアームの制御において、軌道計画に基づいてアームのジョイント部のトルクを制御し、アームを目標の状態とする場合に、アームの位置及び角度のみの軌道計画では、ジョイント部のトルクを制御することはできない。ジョイント部のトルクを制御するには、アームの角度及び角速度を含む状態空間(位相空間)の軌道計画を作成する必要がある。
【0003】
位相空間上での状態遷移を取り扱うための手法として、Rapidly-Exploring Random Trees (RRT) を用いた手法(非特許文献1)がある。しかし、RRTは確率的手法であるため必ずしもコスト最小に近い運動を計画できるとは限らない。また、状態空間の量子化を利用したTazaki の手法(非特許文献2)があるが、この手法は遷移を連続的に扱っておらず、強い線形性の仮定が要求されるため、適用できる機械の種類が限定される。
【0004】
そこで発明者らによって、連続的な探索により準コスト最小運動を計画できる手法として、位相空間の分割と探索木の枝の集約を用いた運動計画手法が提案されている(非特許文献3)。この手法によれば、連続的な探索により、動力学的な拘束条件のもとで与えられた初期状態から目標状態の集合までの準コスト最小運動を短時間で計画できる。しかし、この手法においては、位相空間の分割の際に、各軸に均一な分割を設定し、設計者が粒度を個別に決定していた。また、運動コストを最小化するための効果的な分割の構成方法は実現されていなかった。
【0005】
このように、運動コストを最小化するように状態空間を分割し、より精度よく準コスト最小軌道を計画することのできる軌道計画方法、軌道計画システム及び軌道計画・制御システムは開発されていなかった。
【先行技術文献】
【非特許文献】
【0006】
【非特許文献1】S. M. LaValle and J. J. Kuffner.:”Randomized Kinodynamic Planning,”Journal of Robotics Research, Vol. 20, No. 5, pp.378-400,(2001).
【非特許文献2】Y. Tazaki and J. Imura:”Approximately Bisimilar Discrete Abstractions of Nonlinear Systems Using Variable-resolution Quantizers,”American Control Conference, pp.1015-1020, (2010).
【非特許文献3】C. H. Kim, H. Tsujino and S. Sugano: ”Rapid Short-Time Path Planning for Phase Space,” Journal of Robotics and Mechatronics, Vol. 23, No. 2, (2011).
【発明の概要】
【発明が解決しようとする課題】
【0007】
したがって、運動コストを最小化するように状態空間を分割し、より精度よく準コスト最小軌道を計画することのできる軌道計画方法、軌道計画システム及び軌道計画・制御システムに対するニーズがある。
【課題を解決するための手段】
【0008】
本発明による軌道計画方法は、軌道計画システムによって、物体の状態を目標状態へ制御するための軌道を求める軌道計画方法であって、該物体の状態空間をセルに分割するセル作成部が、所定のセルの数に対して、離散化による近似誤差を最小化するように該状態空間をセルに分割するステップと、探索木作成部が、該状態空間において、該物体の状態遷移に対応する探索木を、該物体の状態に対応する、該探索木の枝のノードがセルに一つずつ含まれるように作成するステップと、軌道作成部が、該探索木を使用して、該物体の現在の状態から目標状態までの経路を定めるステップと、を含む。
【0009】
本発明による軌道計画方法においては、所定のセルの数に対して、離散化による近似誤差を最小化するように状態空間をセルに分割するので、運動コストが最小化され、より精度よく準コスト最小軌道を計画することができる。
【0010】
本発明の一実施形態による軌道計画方法においては、前記分割するステップにおいて、セルの近似誤差を、セル内に含まれる任意の点とセルの中心点に入力を与えた場合の状態遷移先の点の距離の平均として表し、前記状態空間のセルの近似誤差の和が最小となるようにすることによって前記離散化による近似誤差を最小とする。
【0011】
本実施形態によれば、簡単な手順によって離散化による近似誤差を最小とすることができる。
【0012】
本発明の一実施形態による軌道計画方法においては、前記分割するステップが、前記状態空間を均一な基本セルに分割するステップと、前記所定のセルの数に達するまで、基本セルを、セルの近似誤差を最も小さくする軸の方向に分割するステップと、セルの近似誤差の和を小さくするようにセルの分割と結合を繰り返すステップとを含む。
【0013】
本実施形態によれば、基本セルの中で近似誤差が最小となるように分割を実施し、その後、基本セルの間にまたがり、さらに大域的に平均的な近似誤差を小さくするように、分割と結合を繰り返すので、離散化による近似誤差を効率的に最小化することができる。
【0014】
本発明による軌道計画システムは、物体の状態を目標状態へ制御するための軌道を求める軌道計画システムであって、離散化による近似誤差を最小化するように、該物体の状態空間をセルに分割するセル作成部と、該状態空間において、該物体の状態遷移に対応する探索木を、該物体の状態に対応する、該探索木の枝のノードがセルに一つずつ含まれるように作成する探索木作成部と、該探索木を使用して、該物体の現在の状態から目標状態までの軌道を定める軌道作成部と、を備える。
【0015】
本発明による軌道計画システムは、所定のセルの数に対して、離散化による近似誤差を最小化するように状態空間をセルに分割するので、運動コストが最小化され、より精度よく準コスト最小軌道を計画することができる。
【0016】
本発明による軌道計画・制御システムは、本発明による軌道計画システムと、該軌道計画システムが定めた軌道を実現する軌道制御部とを備えている。
【0017】
本発明による軌道計画・制御システムは、本発明による軌道計画システムによってより精度よく計画された準コスト最小軌道を実現することができる。
【図面の簡単な説明】
【0018】
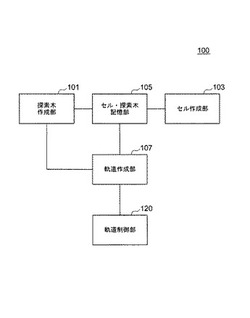
【図1】本発明の一実施形態による軌道計画システムの構成を示す図である。
【図2】二重倒立振子の構成を示す図である。
【図3】本実施形態による軌道計画法を説明するための流れ図である。
【図4】分割された位相空間の例を示す図である。
【図5】図3のステップS020及びステップS030の動作を説明するための図である。
【図6】図3のステップS050及びステップS060の動作を説明するための図である。
【図7】セルの近似誤差の計算方法を説明するための図である。
【図8】セル作成部によって、位相空間を分割してセルを作成する方法を示す流れ図である。
【図9】図8のステップS1020の詳細を説明するための流れ図である。
【図10】図8のステップS1030の詳細を説明するための流れ図である。
【図11】二重倒立振子の第1の初期状態を示す図である。
【図12】二重倒立振子の第2の初期状態を示す図である。
【図13】状態数(最終的なセルの数)を204と設定した場合に、均一分割及び不均一分割の、位置姿勢セル内
【数1】

における速度空間の断面を示す図である。
【図14】セルの数とシミュレーションによって得られた平均運動時間との関係を示す図である。
【図15】状態数が、164、204、244及び284のそれぞれの場合について、3種類の均一分割を使用した場合と図8乃至図10にしたがって分割を行った場合の結果を示す図である。
【発明を実施するための形態】
【0019】
図1は、本発明の一実施形態による軌道計画システム100の構成を示す図である。軌道計画システム100は、ロボットのアームなどの物体の状態を目標状態とするための、状態空間における軌道を求めるシステムである。軌道計画システム100は、状態空間上の物体の位置、すなわち状態に対応する枝を備えた探索木を作成する探索木作成部101と、状態空間を分割して複数のセルを作成するセル作成部103と、セル及び探索木を記憶するセル・探索木記憶部105と、探索木から、物体の状態空間における軌道を作成する軌道作成部107と、を備える。さらに、作成された軌道にしたがって物体の動きを制御する軌道制御部120を追加すれば、軌道計画・制御システムが得られる。各構成部の機能の詳細については、後で説明する。
【0020】
図2は、二重倒立振子200の構成を示す図である。以下の実施形態においては、物体を2次元平面内で運動する二重倒立振子200として説明を行なう。二重倒立振子200は、重心203を有する第1リンク205と、重心209を有する第2リンク211と、第1リンク205を回転可能に固定点に接続する第1関節(ジョイント)201と、第1リンク205及び第2リンク211を回転可能に接続する第2関節207と、から構成される。
【0021】
二重倒立振子200の運動は、第1関節201及び第2関節207に与えるトルクによって定まり、第1リンク205のX軸に対する角度
【数2】

第2リンク211の第1リンク205に対する角度
【数3】

及びこれらの角速度
【数4】

によって表現される。そこで、本実施形態において、状態空間として以下の位相空間を採用する。
【数5】

【0022】
図3は、本実施形態による軌道計画方法を説明するための流れ図である。
【0023】
図3のステップS005において、セル作成部103が、位相空間を分割し複数のセルを作成しておく。セル作成部の動作については後で詳細に説明する。
【0024】
図4は、分割された位相空間の例を示す図である。図4は、簡単のために位相空間を2次元空間として表している。また、図4においては、図を簡略にするため、想定される角度及び角速度の範囲を等分割したセルが示されている。位相空間の分割方法については後で詳細に説明する。
【0025】
図3のステップS010において、探索木作成部101が、二重倒立振子200の現在の状態及び目標状態を得る。ここで、状態は、位相空間上の位置に対応する。
【0026】
図3のステップS020において、探索木作成部101が、位相空間において、現在の状態の位置を探索木の根として定める。
【0027】
図3のステップS030において、探索木作成部101が、位相空間において、所定の時間間隔後の次の状態の位置を、探索木の枝のノードとして定める。所定の時間間隔後の次の状態の位置は、運動方程式や動力学シミュレータによって定める。上述のように、二重倒立振子200の運動は、第1関節201及び第2関節207に与えるトルクによって定まるので、所定の時間間隔に第1関節201及び第2関節207に与えるトルクを定めれば、二重倒立振子200の、所定の時間間隔後の次の状態が定まる。そこで、所定の時間間隔に第1関節201及び第2関節207に与えるトルクを最大値と最小値との間で、所定の増分で変化させながら、それぞれの場合に対応する次の状態を求めてもよい。この場合に、トルクを最大値と最小値との間で、所定の増分で変化させながら、幅優先探索により網羅的に探索を行なってもよい。
【0028】
図5は、図3のステップS020及びステップS030の動作を説明するための図である。なお、図5は、簡単のために位相空間を2次元空間として表している。現在の状態にある、二重倒立振子200に所定の時間間隔に3個の異なるトルク
【数6】

を与えることにより、3個の異なる次の状態が定まる。探索木作成部101は、これらの状態を探索木の枝のノードとする。さらに、生成された枝のノードが示すそれぞれの状態に対して、3個の異なるトルク
【数7】

を与えることにより、3個の異なる、さらに次の状態が定まる。
【0029】
図3のステップS040において、探索木作成部101は、探索木の枝の集約を行う。探索木作成部101が、探索木を作成する場合に、上述のように、根または枝から派生させる枝の数をNとし、木の深さをMとすると、木の深さMのレベルで探索の対象となる枝の数はNMとなる。そこで、探索木作成部101は、上述のセルを利用して、派生させた枝を集約する。具体的に探索木作成部101は、図3のステップS040において、以下の処理を行う。
【0030】
探索木作成部101は、派生させた次の状態が位相空間のどのセルに属するか定める。つぎに、探索木作成部101は、そのセルに属する状態が、枝のノードとしてすでに登録されているかどうか判断する。登録されていなければ、ステップS045に進む。登録されていれば、ステップS060に進む。
【0031】
図3のステップS045において、探索木作成部101は、派生させた状態が身体制約及び環境制約を満たすかどうか判断する。身体制約とは、一例として、ロボットの身体の部材に相当する第1及び第2のリンクが、たとえばお互いに衝突しないために設けられる角度の制約である。また、環境制約とは、身体の部材に相当する第1及び第2のリンクが、たとえば外部の障害物に衝突しないように設けられる角度の制約である。次の状態が身体制約及び環境制約を満たせば、ステップS050に進む。身体制約及び環境制約のいずれかを満たさなければ、ステップS060に進む。
【0032】
図3のステップS050において、探索木作成部101は、派生させた状態を枝のノードとして登録する。
【0033】
図3のステップS060において、探索木作成部101は、探索木作成部101が派生させた枝のノードに対応する次の状態を破棄する。
【0034】
図6は、図3のステップS050及びステップS060の動作を説明するための図である。枝のノードは、原則として1個のセル内には1個しか存在しない。探索木作成部101は、枝のノード(図6の実線で示した円)がすでに存在するセルにノードが位置する新たな枝を破棄する。すなわち、位相空間上の位置が近い状態は集約される。このように、従来の探索木の枝を、セルを使用して集約することによって、計算コストを大幅に低減することができる。
【0035】
図3のステップS070において、探索木作成部101は、探索が終了したかどうか判断する。探索木作成部101は、探索木の所定の深さまでの探索を終えた場合、あるいは所定時間の推移まで探索を終えた場合に探索が終了したと判断してもよい。探索が終了したと判断された場合には、ステップS080に進む。探索が終了していないと判断された場合には、ステップS030に戻り、探索が継続される。
【0036】
図3のステップS080において、軌道作成部107は、枝のノードが表す状態の中から、目標状態との位相空間上の距離が最も近い状態を選択し、この状態を最良状態とする(最終状態最適化の場合)。あるいは、軌道作成部107は、枝のノードが表す状態の中から、目標状態との位相空間上の距離が所定値以下であり、探索木の深さが最も浅い枝に対応する状態を選択し、この状態を最良状態とする(到達時間最適化の場合)。軌道作成部107は、最良状態から現在の状態(初期状態)まで、探索木の枝の経路を求めることにより現在の状態から最良状態に至る軌道を求める。このようにして軌道計画が求まる。たとえば、ロボットは、このようにして求めた軌道計画にしたがってアームを制御することにより、アームの最終状態を最適化し、あるいは、目標状態への到達時間を最適化することができる。
【0037】
上記の実施形態において、探索木作成部101は、現在の状態の位置を探索木の根として探索木を作成した。別の実施形態において、探索木作成部103が、目標状態を探索木の根として探索木を作成するように構成してもよい。
【0038】
本発明による軌道計画方法について、本明細書では、説明を簡単にするために、物体を二重倒立振子としている。しかし、本発明の、既知状態登録木を使用する考え方は、任意の物体の状態空間における軌道計画方法に適用することができる。
【0039】
ここで、セル作成部103の動作について説明する。セル作成103部は、所定のセルの数に対して、離散化による近似誤差を最小とするように状態空間(位相空間)を分割してセルを作成する。ここで、離散化とはセルによる状態の集約を意味する。
【0040】
最初に近似誤差について説明する。図3のステップS040における状態の集約は、位相空間上の点
【数8】

のユークリッド距離
【数9】

が十分に小さい場合、これらの状態に入力uを与えてΔt後に遷移する先の位相空間上の点
【数10】

の距離
【数11】

はやはり近いので、近い状態
【数12】

からの探索では、ほぼ同じ状態遷移系列が得られるという仮定に基づいている。ここで、Δt後の状態は以下の式で表せる。
【数13】

である。
【0041】
同一セル内の状態(位相空間上の点)xから探索して得られる系列が、セルの中心点xμから探索して得られる系列に近似される場合、セルの近似誤差の尺度として同じ入力u(t)に対するΔt後の遷移状態
【数14】

の距離が利用できる。したがって、入力u(t)に対するセルの近似誤差の尺度は、セル内に含まれる任意の状態とセルの中心点
【数15】

の状態遷移先の距離をセル内領域全体
【数16】

で平均することにより表すことができる。こうして求めた入力u(t)に対する近似誤差の尺度について、とりうる入力の集合Uについて平均をとると、セルの近似誤差は以下の式で表すことができる。
【数17】

【0042】
図7は、セルの近似誤差の計算方法を説明するための図である。
【0043】
式(2)のセルの近似誤差を計算するために、本実施形態においては、セルの代表点について
【数18】

を計算し、平均をとる方法を採用する。図7に示すように、各軸方向の最大座標の点と最小座標の点をそれぞれ代表点とし、以下の式によりセルの近似誤差を計算する。ここで、Nは機械モデルの自由度であり、本実施形態においては、N=2である。
【数19】

【0044】
つぎに、上記の手順によって求めたセルの近似誤差を使用して、セル作成部103によって、位相空間を分割してセルを作成する方法について説明する。
【0045】
図8は、セル作成部103によって、位相空間を分割してセルを作成する方法を示す流れ図である。
【0046】
図8のステップS1010において、セル作成部103は、状態空間を均一な基本セルに分割する。基本セルの数は、最終的なセルの数よりも小さくする。基本セルの分割粒度は、全ての軸方向で同じ値としてもよい。
【0047】
図8のステップS1020において、セル作成部103は、全ての基本セルをセルの近似誤差を最小とする方向に分割する。
【0048】
図9は、図8のステップS1020の詳細を説明するための流れ図である。
【0049】
図9のステップS1210において、セル作成部103は、総分割数、すなわち、最終的なセルの数を取得する。
【0050】
図9のステップS1220において、セル作成部103は、全ての基本セルのリストを作成する。
【0051】
図9のステップS1230において、セル作成部103は、リストの先頭のセルを各軸方向に仮想的に分割した後のセルの近似誤差を求める。
【0052】
図9のステップS1240において、セル作成部103は、分割後の近似誤差が最小となる軸方向にセルを分割する。ここで、分割には、文献(Y. Tazaki and J. Imura:”Approximately Bisimilar Discrete Abstractions of Nonlinear Systems Using Variable-resolution Quantizers,”American Control Conference, pp.1015-1020, (2010).)などでも使用されている二分木を基にした分割構造を使用する。この構造は、指定したセルを二つの子セルに分割する細分化の機能を備えている。
【0053】
図9のステップS1250において、セル作成部103は、分割されたセルをリストの末尾に追加し、先頭のセルをリストから削除する。
【0054】
図9のステップS1260において、セル作成部103は、セルの数が最終的なセルの数に達したかどうか判断する。セルの数が最終的なセルの数に達していれば処理を終了する。セルの数が最終的なセルの数に達していなければ、ステップS1230に戻る。
【0055】
このように、図8のステップS1020において、基本セルの中で近似誤差が最小となるように分割が行われる。
【0056】
図8のステップS1030において、セル作成部103はセルの分割と結合を繰り返す。
【0057】
図10は、図8のステップS1030の詳細を説明するための流れ図である。
【0058】
図10のステップS1410において、セル作成部103は、分割構造の末端のすべての子セルのリスト(以下において、リストAと呼称する)及びその一階層上のすべての親セルのリスト(以下において、リストBと呼称する)を作成する。
【0059】
図10のステップS1420において、セル作成部103は、リストA及びリストBの対応するセルについて近似誤差減少量を計算する。近似誤差減少量は以下の式で表せる。
【数20】

ここで、右辺の第1項は親セルの近似誤差であり、右辺の第2項及び第3項は子セルの近似誤差である。iは、i軸方向の分割であることを示す。
【0060】
図10のステップS1430において、セル作成部103は、リストAを近似誤差減少量の降順にソートする。
【0061】
図10のステップS1440において、セル作成部103は、リストBを近似誤差減少量の昇順にソートする。
【0062】
図10のステップS1450において、セル作成部103は、リストAの先頭に位置するセルの近似誤差減少量が、リストBの先頭に位置するセルの近似誤差減少量よりも大きいどうか判断する。リストAの先頭に位置するセルの近似誤差減少量が、リストBの先頭に位置するセルの近似誤差減少量よりも大きければ、ステップS1460に進む。そうでなければ処理を終了する。
【0063】
図10のステップS1460において、セル作成部103は、リストAの先頭に位置するセルを、分割後のセルの近似誤差が最小となる軸方向に分割し、リストBの先頭に位置するセルの子セルを結合する。
【0064】
図10のステップS1470において、セル作成部103は、新たなセルの近似誤差減少量を計算し、リストAに追加し、リストA及びリストBを更新する。
【0065】
このように、図8のステップS1030において、位相空間(状態空間)全体での近似誤差の平均が小さくなるように分割と結合が繰り返される。ステップS1030において、セルの総数は変化しない。
【0066】
図8のステップS1020においては、基本セルの中で近似誤差が最小となるように分割が行われる。しかし、全基本セルについて、個々の分割数はほぼ一定となっているため、この段階では局所的な不均一分割が生成される。そこで、基本セルの間にまたがり、さらに大域的に平均的な近似誤差を小さくする処理として、分割と結合を繰り返す図8のステップS1030の処理を行う。ステップS1030では、セルの重要度を空間全体の体積
【数21】

に占めるセルの体積
【数22】

で表し、この重要度で重みづけられた空間全体での近似誤差の総和を最小化するように分割を再構成する。正確には、この処理では近似誤差の総和は局所解へと収束する。
【数23】

【0067】
つぎに、本実施形態の軌道計画システムの効果を確認するための、二重倒立振子200のシミュレーション実験について説明する。二重倒立振子200の第1リンク205のリンク長は、l1であり、質量は、m1であり、重心位置203はリンクの中央である。二重倒立振子200の第2リンク211のリンク長は、l2であり、質量は、m2であり、重心位置209はリンクの中央である。また、重力加速度をgとする。
【0068】
表1は、使用した二重倒立振子200のパラメータを示す。
【表1】

【0069】
二重倒立振子200の運動方程式は、以下のとおりである。
【数24】

関節角度と重力の関係に対する理解を容易にするために、以下のように座標を変更した。
【数25】

【0070】
表2は、本実施形態の軌道計画システムのパラメータを示す表である。
【表2】

【0071】
シミュレータの刻み時間幅Δtは50ミリ秒とし、最大計画運動時間は10秒とした。運動のコストは運動時間として、各種境界条件のもとで準最短時間運動を求めた。また、距離の関数として以下の式を設定した。
【数26】

wpi及びwviは各軸iの重み定数であり、本シミュレーションでは、各関節ともwpi及びwviにはそれぞれ1.0及び0.2を使用した。
【0072】
本シミュレーションでは、第1リンク205及び第2リンク211がともに下がって静止した第1の初期状態及びともに倒立して静止した第2の初期状態を設定した。
【0073】
図11は、二重倒立振子200の第1の初期状態を示す図である。二重倒立振子200の第1の初期状態の座標は以下のとおりである。
【数27】

【0074】
図12は、二重倒立振子200の第2の初期状態を示す図である。二重倒立振子200の第2の初期状態の座標は以下のとおりである。
【数28】

【0075】
本シミュレーションにおいては、第1及び第2の初期状態から、ランダムサンプリングした目標状態への運動を計画し、計画された運動のコスト、すなわち運動時間を調べた。100000個の目標状態からなるサンプルデータを作成し、これらの目標状態までの運動時間の平均を様々な分割条件について比較した。
【0076】
また、姿勢空間の分割粒度を均一に固定し、速度方向にのみ上述の方法によって不均一に分割を行った。その理由は、障害物が姿勢空間上の拘束条件として表されるためであり、また、距離のパラメータの設定の影響を小さく抑えるためである。基本セルの分割粒度は、すべての軸方向に同じ値を設定した。
【0077】
図13は、状態数(最終的なセルの数)を204と設定した場合の、一姿勢セル内
【数29】

における速度空間の断面を示す図である。図13(a)は、各姿勢方向及び速度方向に対して同じ分割粒度を設定して分割を行った場合を示し、図13(b)は、姿勢空間の分割粒度を均一に固定し、速度方向にのみ上述の方法によって不均一に分割を行った場合を示す。
【0078】
図14は、セルの数とシミュレーションによって得られた平均運動時間との関係を示す図である。図14において、横軸はセルの数(総分割数)を表し、縦軸は平均時間を表す。図14において、「均一セル」は、各姿勢方向及び速度方向に対して同じ分割粒度を設定して分割を行った場合を示し、「本発明のセル」は、姿勢空間の分割粒度を均一に固定し、速度方向にのみ上述の方法によって不均一に分割を行った場合を示す。状態数(最終的なセルの数)が増えれば近似誤差は小さくなり、より短時間で遷移する運動を発見できることが確認できる。状態数が増えるにつれた、真の最短運動時間の平均値である、ある値に収束していくことが予想される。また、全ての分割条件について、「本発明のセル」の場合は、「均一セル」を使用した場合に比較してより短時間で遷移する運動を発見できることが確認できる。
【0079】
図15は、状態数(セルの数)が、164、204、244及び284のそれぞれの場合について、3種類の軸方向に均一な分割粒度を設定して分割を行った場合と姿勢空間の分割粒度を均一に固定し、速度方向にのみ上述の方法によって不均一に分割を行った場合の結果を示す図である。図15において、「均一1」、「均一2」及び「均一3」は、同じ状態数となるように、
【数30】

方向の分割粒度を均一とし、その比を、それぞれ1:4、1:1及び4:1に設定した場合を示す。また、「本発明」は、姿勢空間の分割粒度を均一に固定し、速度方向にのみ上述の方法によって不均一に分割を行った場合を示す。図15の縦軸は、平均時間の割合(コスト)を表す。ここで、平均時間の割合(コスト)は、状態数304の場合の平均時間の値を最適値として、それぞれの場合の平均時間とこの最適値との差によって表した。縦軸の値が小さいほど平均時間の割合(コスト)が小さい。割合(コスト)は、状態数によって変化する。「均一1」、「均一2」及び「均一3」の割合(コスト)を比較すると、全ての状態数の場合に他よりも割合(コスト)が小さいものは存在しない。これに対して、「本発明」の割合(コスト)は、全ての状態数の場合に、「均一1」、「均一2」及び「均一3」の割合(コスト)よりも小さい。
【0080】
このように、本発明の軌道計画システム及び軌道計画方法によれば、同じ状態数で、よりコストの小さい運動を精度良く発見することができる。また、本発明の軌道計画システムを含む本発明の軌道計画・制御システムは、本発明の軌道計画システムが作成した軌道をフィードバック制御などによって実現することにより、よりコストの小さい運動を実現することができる。本発明の枠組みは、機械状態を位相空間で扱う汎用的なものであるので、ロボット、自動車、航空機、ロケットの運動計画など様々な分野に広く応用することができる。
【符号の説明】
【0081】
101…探索木作成部、103…セル作成部、105…セル・。探索木記憶部、107…軌道作成部、120…軌道制御部
【技術分野】
【0001】
本発明は、物体の、目標状態に至る状態遷移系列を作成する、軌道計画方法、軌道計画システム及び上記軌道計画システムを備えた軌道計画・制御システムに関する。
【背景技術】
【0002】
たとえば、ロボットのアームの制御において、軌道計画に基づいてアームのジョイント部のトルクを制御し、アームを目標の状態とする場合に、アームの位置及び角度のみの軌道計画では、ジョイント部のトルクを制御することはできない。ジョイント部のトルクを制御するには、アームの角度及び角速度を含む状態空間(位相空間)の軌道計画を作成する必要がある。
【0003】
位相空間上での状態遷移を取り扱うための手法として、Rapidly-Exploring Random Trees (RRT) を用いた手法(非特許文献1)がある。しかし、RRTは確率的手法であるため必ずしもコスト最小に近い運動を計画できるとは限らない。また、状態空間の量子化を利用したTazaki の手法(非特許文献2)があるが、この手法は遷移を連続的に扱っておらず、強い線形性の仮定が要求されるため、適用できる機械の種類が限定される。
【0004】
そこで発明者らによって、連続的な探索により準コスト最小運動を計画できる手法として、位相空間の分割と探索木の枝の集約を用いた運動計画手法が提案されている(非特許文献3)。この手法によれば、連続的な探索により、動力学的な拘束条件のもとで与えられた初期状態から目標状態の集合までの準コスト最小運動を短時間で計画できる。しかし、この手法においては、位相空間の分割の際に、各軸に均一な分割を設定し、設計者が粒度を個別に決定していた。また、運動コストを最小化するための効果的な分割の構成方法は実現されていなかった。
【0005】
このように、運動コストを最小化するように状態空間を分割し、より精度よく準コスト最小軌道を計画することのできる軌道計画方法、軌道計画システム及び軌道計画・制御システムは開発されていなかった。
【先行技術文献】
【非特許文献】
【0006】
【非特許文献1】S. M. LaValle and J. J. Kuffner.:”Randomized Kinodynamic Planning,”Journal of Robotics Research, Vol. 20, No. 5, pp.378-400,(2001).
【非特許文献2】Y. Tazaki and J. Imura:”Approximately Bisimilar Discrete Abstractions of Nonlinear Systems Using Variable-resolution Quantizers,”American Control Conference, pp.1015-1020, (2010).
【非特許文献3】C. H. Kim, H. Tsujino and S. Sugano: ”Rapid Short-Time Path Planning for Phase Space,” Journal of Robotics and Mechatronics, Vol. 23, No. 2, (2011).
【発明の概要】
【発明が解決しようとする課題】
【0007】
したがって、運動コストを最小化するように状態空間を分割し、より精度よく準コスト最小軌道を計画することのできる軌道計画方法、軌道計画システム及び軌道計画・制御システムに対するニーズがある。
【課題を解決するための手段】
【0008】
本発明による軌道計画方法は、軌道計画システムによって、物体の状態を目標状態へ制御するための軌道を求める軌道計画方法であって、該物体の状態空間をセルに分割するセル作成部が、所定のセルの数に対して、離散化による近似誤差を最小化するように該状態空間をセルに分割するステップと、探索木作成部が、該状態空間において、該物体の状態遷移に対応する探索木を、該物体の状態に対応する、該探索木の枝のノードがセルに一つずつ含まれるように作成するステップと、軌道作成部が、該探索木を使用して、該物体の現在の状態から目標状態までの経路を定めるステップと、を含む。
【0009】
本発明による軌道計画方法においては、所定のセルの数に対して、離散化による近似誤差を最小化するように状態空間をセルに分割するので、運動コストが最小化され、より精度よく準コスト最小軌道を計画することができる。
【0010】
本発明の一実施形態による軌道計画方法においては、前記分割するステップにおいて、セルの近似誤差を、セル内に含まれる任意の点とセルの中心点に入力を与えた場合の状態遷移先の点の距離の平均として表し、前記状態空間のセルの近似誤差の和が最小となるようにすることによって前記離散化による近似誤差を最小とする。
【0011】
本実施形態によれば、簡単な手順によって離散化による近似誤差を最小とすることができる。
【0012】
本発明の一実施形態による軌道計画方法においては、前記分割するステップが、前記状態空間を均一な基本セルに分割するステップと、前記所定のセルの数に達するまで、基本セルを、セルの近似誤差を最も小さくする軸の方向に分割するステップと、セルの近似誤差の和を小さくするようにセルの分割と結合を繰り返すステップとを含む。
【0013】
本実施形態によれば、基本セルの中で近似誤差が最小となるように分割を実施し、その後、基本セルの間にまたがり、さらに大域的に平均的な近似誤差を小さくするように、分割と結合を繰り返すので、離散化による近似誤差を効率的に最小化することができる。
【0014】
本発明による軌道計画システムは、物体の状態を目標状態へ制御するための軌道を求める軌道計画システムであって、離散化による近似誤差を最小化するように、該物体の状態空間をセルに分割するセル作成部と、該状態空間において、該物体の状態遷移に対応する探索木を、該物体の状態に対応する、該探索木の枝のノードがセルに一つずつ含まれるように作成する探索木作成部と、該探索木を使用して、該物体の現在の状態から目標状態までの軌道を定める軌道作成部と、を備える。
【0015】
本発明による軌道計画システムは、所定のセルの数に対して、離散化による近似誤差を最小化するように状態空間をセルに分割するので、運動コストが最小化され、より精度よく準コスト最小軌道を計画することができる。
【0016】
本発明による軌道計画・制御システムは、本発明による軌道計画システムと、該軌道計画システムが定めた軌道を実現する軌道制御部とを備えている。
【0017】
本発明による軌道計画・制御システムは、本発明による軌道計画システムによってより精度よく計画された準コスト最小軌道を実現することができる。
【図面の簡単な説明】
【0018】
【図1】本発明の一実施形態による軌道計画システムの構成を示す図である。
【図2】二重倒立振子の構成を示す図である。
【図3】本実施形態による軌道計画法を説明するための流れ図である。
【図4】分割された位相空間の例を示す図である。
【図5】図3のステップS020及びステップS030の動作を説明するための図である。
【図6】図3のステップS050及びステップS060の動作を説明するための図である。
【図7】セルの近似誤差の計算方法を説明するための図である。
【図8】セル作成部によって、位相空間を分割してセルを作成する方法を示す流れ図である。
【図9】図8のステップS1020の詳細を説明するための流れ図である。
【図10】図8のステップS1030の詳細を説明するための流れ図である。
【図11】二重倒立振子の第1の初期状態を示す図である。
【図12】二重倒立振子の第2の初期状態を示す図である。
【図13】状態数(最終的なセルの数)を204と設定した場合に、均一分割及び不均一分割の、位置姿勢セル内
【数1】

における速度空間の断面を示す図である。
【図14】セルの数とシミュレーションによって得られた平均運動時間との関係を示す図である。
【図15】状態数が、164、204、244及び284のそれぞれの場合について、3種類の均一分割を使用した場合と図8乃至図10にしたがって分割を行った場合の結果を示す図である。
【発明を実施するための形態】
【0019】
図1は、本発明の一実施形態による軌道計画システム100の構成を示す図である。軌道計画システム100は、ロボットのアームなどの物体の状態を目標状態とするための、状態空間における軌道を求めるシステムである。軌道計画システム100は、状態空間上の物体の位置、すなわち状態に対応する枝を備えた探索木を作成する探索木作成部101と、状態空間を分割して複数のセルを作成するセル作成部103と、セル及び探索木を記憶するセル・探索木記憶部105と、探索木から、物体の状態空間における軌道を作成する軌道作成部107と、を備える。さらに、作成された軌道にしたがって物体の動きを制御する軌道制御部120を追加すれば、軌道計画・制御システムが得られる。各構成部の機能の詳細については、後で説明する。
【0020】
図2は、二重倒立振子200の構成を示す図である。以下の実施形態においては、物体を2次元平面内で運動する二重倒立振子200として説明を行なう。二重倒立振子200は、重心203を有する第1リンク205と、重心209を有する第2リンク211と、第1リンク205を回転可能に固定点に接続する第1関節(ジョイント)201と、第1リンク205及び第2リンク211を回転可能に接続する第2関節207と、から構成される。
【0021】
二重倒立振子200の運動は、第1関節201及び第2関節207に与えるトルクによって定まり、第1リンク205のX軸に対する角度
【数2】

第2リンク211の第1リンク205に対する角度
【数3】

及びこれらの角速度
【数4】

によって表現される。そこで、本実施形態において、状態空間として以下の位相空間を採用する。
【数5】

【0022】
図3は、本実施形態による軌道計画方法を説明するための流れ図である。
【0023】
図3のステップS005において、セル作成部103が、位相空間を分割し複数のセルを作成しておく。セル作成部の動作については後で詳細に説明する。
【0024】
図4は、分割された位相空間の例を示す図である。図4は、簡単のために位相空間を2次元空間として表している。また、図4においては、図を簡略にするため、想定される角度及び角速度の範囲を等分割したセルが示されている。位相空間の分割方法については後で詳細に説明する。
【0025】
図3のステップS010において、探索木作成部101が、二重倒立振子200の現在の状態及び目標状態を得る。ここで、状態は、位相空間上の位置に対応する。
【0026】
図3のステップS020において、探索木作成部101が、位相空間において、現在の状態の位置を探索木の根として定める。
【0027】
図3のステップS030において、探索木作成部101が、位相空間において、所定の時間間隔後の次の状態の位置を、探索木の枝のノードとして定める。所定の時間間隔後の次の状態の位置は、運動方程式や動力学シミュレータによって定める。上述のように、二重倒立振子200の運動は、第1関節201及び第2関節207に与えるトルクによって定まるので、所定の時間間隔に第1関節201及び第2関節207に与えるトルクを定めれば、二重倒立振子200の、所定の時間間隔後の次の状態が定まる。そこで、所定の時間間隔に第1関節201及び第2関節207に与えるトルクを最大値と最小値との間で、所定の増分で変化させながら、それぞれの場合に対応する次の状態を求めてもよい。この場合に、トルクを最大値と最小値との間で、所定の増分で変化させながら、幅優先探索により網羅的に探索を行なってもよい。
【0028】
図5は、図3のステップS020及びステップS030の動作を説明するための図である。なお、図5は、簡単のために位相空間を2次元空間として表している。現在の状態にある、二重倒立振子200に所定の時間間隔に3個の異なるトルク
【数6】

を与えることにより、3個の異なる次の状態が定まる。探索木作成部101は、これらの状態を探索木の枝のノードとする。さらに、生成された枝のノードが示すそれぞれの状態に対して、3個の異なるトルク
【数7】

を与えることにより、3個の異なる、さらに次の状態が定まる。
【0029】
図3のステップS040において、探索木作成部101は、探索木の枝の集約を行う。探索木作成部101が、探索木を作成する場合に、上述のように、根または枝から派生させる枝の数をNとし、木の深さをMとすると、木の深さMのレベルで探索の対象となる枝の数はNMとなる。そこで、探索木作成部101は、上述のセルを利用して、派生させた枝を集約する。具体的に探索木作成部101は、図3のステップS040において、以下の処理を行う。
【0030】
探索木作成部101は、派生させた次の状態が位相空間のどのセルに属するか定める。つぎに、探索木作成部101は、そのセルに属する状態が、枝のノードとしてすでに登録されているかどうか判断する。登録されていなければ、ステップS045に進む。登録されていれば、ステップS060に進む。
【0031】
図3のステップS045において、探索木作成部101は、派生させた状態が身体制約及び環境制約を満たすかどうか判断する。身体制約とは、一例として、ロボットの身体の部材に相当する第1及び第2のリンクが、たとえばお互いに衝突しないために設けられる角度の制約である。また、環境制約とは、身体の部材に相当する第1及び第2のリンクが、たとえば外部の障害物に衝突しないように設けられる角度の制約である。次の状態が身体制約及び環境制約を満たせば、ステップS050に進む。身体制約及び環境制約のいずれかを満たさなければ、ステップS060に進む。
【0032】
図3のステップS050において、探索木作成部101は、派生させた状態を枝のノードとして登録する。
【0033】
図3のステップS060において、探索木作成部101は、探索木作成部101が派生させた枝のノードに対応する次の状態を破棄する。
【0034】
図6は、図3のステップS050及びステップS060の動作を説明するための図である。枝のノードは、原則として1個のセル内には1個しか存在しない。探索木作成部101は、枝のノード(図6の実線で示した円)がすでに存在するセルにノードが位置する新たな枝を破棄する。すなわち、位相空間上の位置が近い状態は集約される。このように、従来の探索木の枝を、セルを使用して集約することによって、計算コストを大幅に低減することができる。
【0035】
図3のステップS070において、探索木作成部101は、探索が終了したかどうか判断する。探索木作成部101は、探索木の所定の深さまでの探索を終えた場合、あるいは所定時間の推移まで探索を終えた場合に探索が終了したと判断してもよい。探索が終了したと判断された場合には、ステップS080に進む。探索が終了していないと判断された場合には、ステップS030に戻り、探索が継続される。
【0036】
図3のステップS080において、軌道作成部107は、枝のノードが表す状態の中から、目標状態との位相空間上の距離が最も近い状態を選択し、この状態を最良状態とする(最終状態最適化の場合)。あるいは、軌道作成部107は、枝のノードが表す状態の中から、目標状態との位相空間上の距離が所定値以下であり、探索木の深さが最も浅い枝に対応する状態を選択し、この状態を最良状態とする(到達時間最適化の場合)。軌道作成部107は、最良状態から現在の状態(初期状態)まで、探索木の枝の経路を求めることにより現在の状態から最良状態に至る軌道を求める。このようにして軌道計画が求まる。たとえば、ロボットは、このようにして求めた軌道計画にしたがってアームを制御することにより、アームの最終状態を最適化し、あるいは、目標状態への到達時間を最適化することができる。
【0037】
上記の実施形態において、探索木作成部101は、現在の状態の位置を探索木の根として探索木を作成した。別の実施形態において、探索木作成部103が、目標状態を探索木の根として探索木を作成するように構成してもよい。
【0038】
本発明による軌道計画方法について、本明細書では、説明を簡単にするために、物体を二重倒立振子としている。しかし、本発明の、既知状態登録木を使用する考え方は、任意の物体の状態空間における軌道計画方法に適用することができる。
【0039】
ここで、セル作成部103の動作について説明する。セル作成103部は、所定のセルの数に対して、離散化による近似誤差を最小とするように状態空間(位相空間)を分割してセルを作成する。ここで、離散化とはセルによる状態の集約を意味する。
【0040】
最初に近似誤差について説明する。図3のステップS040における状態の集約は、位相空間上の点
【数8】

のユークリッド距離
【数9】

が十分に小さい場合、これらの状態に入力uを与えてΔt後に遷移する先の位相空間上の点
【数10】

の距離
【数11】

はやはり近いので、近い状態
【数12】

からの探索では、ほぼ同じ状態遷移系列が得られるという仮定に基づいている。ここで、Δt後の状態は以下の式で表せる。
【数13】

である。
【0041】
同一セル内の状態(位相空間上の点)xから探索して得られる系列が、セルの中心点xμから探索して得られる系列に近似される場合、セルの近似誤差の尺度として同じ入力u(t)に対するΔt後の遷移状態
【数14】

の距離が利用できる。したがって、入力u(t)に対するセルの近似誤差の尺度は、セル内に含まれる任意の状態とセルの中心点
【数15】

の状態遷移先の距離をセル内領域全体
【数16】

で平均することにより表すことができる。こうして求めた入力u(t)に対する近似誤差の尺度について、とりうる入力の集合Uについて平均をとると、セルの近似誤差は以下の式で表すことができる。
【数17】

【0042】
図7は、セルの近似誤差の計算方法を説明するための図である。
【0043】
式(2)のセルの近似誤差を計算するために、本実施形態においては、セルの代表点について
【数18】

を計算し、平均をとる方法を採用する。図7に示すように、各軸方向の最大座標の点と最小座標の点をそれぞれ代表点とし、以下の式によりセルの近似誤差を計算する。ここで、Nは機械モデルの自由度であり、本実施形態においては、N=2である。
【数19】

【0044】
つぎに、上記の手順によって求めたセルの近似誤差を使用して、セル作成部103によって、位相空間を分割してセルを作成する方法について説明する。
【0045】
図8は、セル作成部103によって、位相空間を分割してセルを作成する方法を示す流れ図である。
【0046】
図8のステップS1010において、セル作成部103は、状態空間を均一な基本セルに分割する。基本セルの数は、最終的なセルの数よりも小さくする。基本セルの分割粒度は、全ての軸方向で同じ値としてもよい。
【0047】
図8のステップS1020において、セル作成部103は、全ての基本セルをセルの近似誤差を最小とする方向に分割する。
【0048】
図9は、図8のステップS1020の詳細を説明するための流れ図である。
【0049】
図9のステップS1210において、セル作成部103は、総分割数、すなわち、最終的なセルの数を取得する。
【0050】
図9のステップS1220において、セル作成部103は、全ての基本セルのリストを作成する。
【0051】
図9のステップS1230において、セル作成部103は、リストの先頭のセルを各軸方向に仮想的に分割した後のセルの近似誤差を求める。
【0052】
図9のステップS1240において、セル作成部103は、分割後の近似誤差が最小となる軸方向にセルを分割する。ここで、分割には、文献(Y. Tazaki and J. Imura:”Approximately Bisimilar Discrete Abstractions of Nonlinear Systems Using Variable-resolution Quantizers,”American Control Conference, pp.1015-1020, (2010).)などでも使用されている二分木を基にした分割構造を使用する。この構造は、指定したセルを二つの子セルに分割する細分化の機能を備えている。
【0053】
図9のステップS1250において、セル作成部103は、分割されたセルをリストの末尾に追加し、先頭のセルをリストから削除する。
【0054】
図9のステップS1260において、セル作成部103は、セルの数が最終的なセルの数に達したかどうか判断する。セルの数が最終的なセルの数に達していれば処理を終了する。セルの数が最終的なセルの数に達していなければ、ステップS1230に戻る。
【0055】
このように、図8のステップS1020において、基本セルの中で近似誤差が最小となるように分割が行われる。
【0056】
図8のステップS1030において、セル作成部103はセルの分割と結合を繰り返す。
【0057】
図10は、図8のステップS1030の詳細を説明するための流れ図である。
【0058】
図10のステップS1410において、セル作成部103は、分割構造の末端のすべての子セルのリスト(以下において、リストAと呼称する)及びその一階層上のすべての親セルのリスト(以下において、リストBと呼称する)を作成する。
【0059】
図10のステップS1420において、セル作成部103は、リストA及びリストBの対応するセルについて近似誤差減少量を計算する。近似誤差減少量は以下の式で表せる。
【数20】

ここで、右辺の第1項は親セルの近似誤差であり、右辺の第2項及び第3項は子セルの近似誤差である。iは、i軸方向の分割であることを示す。
【0060】
図10のステップS1430において、セル作成部103は、リストAを近似誤差減少量の降順にソートする。
【0061】
図10のステップS1440において、セル作成部103は、リストBを近似誤差減少量の昇順にソートする。
【0062】
図10のステップS1450において、セル作成部103は、リストAの先頭に位置するセルの近似誤差減少量が、リストBの先頭に位置するセルの近似誤差減少量よりも大きいどうか判断する。リストAの先頭に位置するセルの近似誤差減少量が、リストBの先頭に位置するセルの近似誤差減少量よりも大きければ、ステップS1460に進む。そうでなければ処理を終了する。
【0063】
図10のステップS1460において、セル作成部103は、リストAの先頭に位置するセルを、分割後のセルの近似誤差が最小となる軸方向に分割し、リストBの先頭に位置するセルの子セルを結合する。
【0064】
図10のステップS1470において、セル作成部103は、新たなセルの近似誤差減少量を計算し、リストAに追加し、リストA及びリストBを更新する。
【0065】
このように、図8のステップS1030において、位相空間(状態空間)全体での近似誤差の平均が小さくなるように分割と結合が繰り返される。ステップS1030において、セルの総数は変化しない。
【0066】
図8のステップS1020においては、基本セルの中で近似誤差が最小となるように分割が行われる。しかし、全基本セルについて、個々の分割数はほぼ一定となっているため、この段階では局所的な不均一分割が生成される。そこで、基本セルの間にまたがり、さらに大域的に平均的な近似誤差を小さくする処理として、分割と結合を繰り返す図8のステップS1030の処理を行う。ステップS1030では、セルの重要度を空間全体の体積
【数21】

に占めるセルの体積
【数22】

で表し、この重要度で重みづけられた空間全体での近似誤差の総和を最小化するように分割を再構成する。正確には、この処理では近似誤差の総和は局所解へと収束する。
【数23】

【0067】
つぎに、本実施形態の軌道計画システムの効果を確認するための、二重倒立振子200のシミュレーション実験について説明する。二重倒立振子200の第1リンク205のリンク長は、l1であり、質量は、m1であり、重心位置203はリンクの中央である。二重倒立振子200の第2リンク211のリンク長は、l2であり、質量は、m2であり、重心位置209はリンクの中央である。また、重力加速度をgとする。
【0068】
表1は、使用した二重倒立振子200のパラメータを示す。
【表1】

【0069】
二重倒立振子200の運動方程式は、以下のとおりである。
【数24】

関節角度と重力の関係に対する理解を容易にするために、以下のように座標を変更した。
【数25】

【0070】
表2は、本実施形態の軌道計画システムのパラメータを示す表である。
【表2】

【0071】
シミュレータの刻み時間幅Δtは50ミリ秒とし、最大計画運動時間は10秒とした。運動のコストは運動時間として、各種境界条件のもとで準最短時間運動を求めた。また、距離の関数として以下の式を設定した。
【数26】

wpi及びwviは各軸iの重み定数であり、本シミュレーションでは、各関節ともwpi及びwviにはそれぞれ1.0及び0.2を使用した。
【0072】
本シミュレーションでは、第1リンク205及び第2リンク211がともに下がって静止した第1の初期状態及びともに倒立して静止した第2の初期状態を設定した。
【0073】
図11は、二重倒立振子200の第1の初期状態を示す図である。二重倒立振子200の第1の初期状態の座標は以下のとおりである。
【数27】

【0074】
図12は、二重倒立振子200の第2の初期状態を示す図である。二重倒立振子200の第2の初期状態の座標は以下のとおりである。
【数28】

【0075】
本シミュレーションにおいては、第1及び第2の初期状態から、ランダムサンプリングした目標状態への運動を計画し、計画された運動のコスト、すなわち運動時間を調べた。100000個の目標状態からなるサンプルデータを作成し、これらの目標状態までの運動時間の平均を様々な分割条件について比較した。
【0076】
また、姿勢空間の分割粒度を均一に固定し、速度方向にのみ上述の方法によって不均一に分割を行った。その理由は、障害物が姿勢空間上の拘束条件として表されるためであり、また、距離のパラメータの設定の影響を小さく抑えるためである。基本セルの分割粒度は、すべての軸方向に同じ値を設定した。
【0077】
図13は、状態数(最終的なセルの数)を204と設定した場合の、一姿勢セル内
【数29】

における速度空間の断面を示す図である。図13(a)は、各姿勢方向及び速度方向に対して同じ分割粒度を設定して分割を行った場合を示し、図13(b)は、姿勢空間の分割粒度を均一に固定し、速度方向にのみ上述の方法によって不均一に分割を行った場合を示す。
【0078】
図14は、セルの数とシミュレーションによって得られた平均運動時間との関係を示す図である。図14において、横軸はセルの数(総分割数)を表し、縦軸は平均時間を表す。図14において、「均一セル」は、各姿勢方向及び速度方向に対して同じ分割粒度を設定して分割を行った場合を示し、「本発明のセル」は、姿勢空間の分割粒度を均一に固定し、速度方向にのみ上述の方法によって不均一に分割を行った場合を示す。状態数(最終的なセルの数)が増えれば近似誤差は小さくなり、より短時間で遷移する運動を発見できることが確認できる。状態数が増えるにつれた、真の最短運動時間の平均値である、ある値に収束していくことが予想される。また、全ての分割条件について、「本発明のセル」の場合は、「均一セル」を使用した場合に比較してより短時間で遷移する運動を発見できることが確認できる。
【0079】
図15は、状態数(セルの数)が、164、204、244及び284のそれぞれの場合について、3種類の軸方向に均一な分割粒度を設定して分割を行った場合と姿勢空間の分割粒度を均一に固定し、速度方向にのみ上述の方法によって不均一に分割を行った場合の結果を示す図である。図15において、「均一1」、「均一2」及び「均一3」は、同じ状態数となるように、
【数30】

方向の分割粒度を均一とし、その比を、それぞれ1:4、1:1及び4:1に設定した場合を示す。また、「本発明」は、姿勢空間の分割粒度を均一に固定し、速度方向にのみ上述の方法によって不均一に分割を行った場合を示す。図15の縦軸は、平均時間の割合(コスト)を表す。ここで、平均時間の割合(コスト)は、状態数304の場合の平均時間の値を最適値として、それぞれの場合の平均時間とこの最適値との差によって表した。縦軸の値が小さいほど平均時間の割合(コスト)が小さい。割合(コスト)は、状態数によって変化する。「均一1」、「均一2」及び「均一3」の割合(コスト)を比較すると、全ての状態数の場合に他よりも割合(コスト)が小さいものは存在しない。これに対して、「本発明」の割合(コスト)は、全ての状態数の場合に、「均一1」、「均一2」及び「均一3」の割合(コスト)よりも小さい。
【0080】
このように、本発明の軌道計画システム及び軌道計画方法によれば、同じ状態数で、よりコストの小さい運動を精度良く発見することができる。また、本発明の軌道計画システムを含む本発明の軌道計画・制御システムは、本発明の軌道計画システムが作成した軌道をフィードバック制御などによって実現することにより、よりコストの小さい運動を実現することができる。本発明の枠組みは、機械状態を位相空間で扱う汎用的なものであるので、ロボット、自動車、航空機、ロケットの運動計画など様々な分野に広く応用することができる。
【符号の説明】
【0081】
101…探索木作成部、103…セル作成部、105…セル・。探索木記憶部、107…軌道作成部、120…軌道制御部
【特許請求の範囲】
【請求項1】
軌道計画システムによって、物体の状態を目標状態へ制御するための軌道を求める軌道計画方法であって、
該物体の状態空間をセルに分割するセル作成部が、所定のセルの数に対して、離散化による近似誤差を最小化するように該状態空間をセルに分割するステップと、
探索木作成部が、該状態空間において、該物体の状態遷移に対応する探索木を、該物体の状態に対応する、該探索木の枝のノードがセルに一つずつ含まれるように作成するステップと、
軌道作成部が、該探索木を使用して、該物体の現在の状態から目標状態までの経路を定めるステップと、を含む、軌道計画方法。
【請求項2】
前記分割するステップにおいて、セルの近似誤差を、セル内に含まれる任意の点とセルの中心点に、入力を与えた場合の状態遷移先の距離の平均として表し、前記状態空間のセルの近似誤差の和が最小となるようにすることによって前記離散化による近似誤差を最小とする請求項1に記載の軌道計画方法。
【請求項3】
前記分割するステップが、前記状態空間を均一な基本セルに分割するステップと、前記所定のセルの数に達するまで、全ての基本セルを、セルの近似誤差を最も小さくする軸の方向に分割するステップと、セルの近似誤差の和を小さくするようにセルの分割と結合を繰り返すステップとを含む請求項1または2に記載の軌道計画方法。
【請求項4】
物体の状態を目標状態へ制御するための軌道を求める軌道計画システムであって、
離散化による近似誤差を最小化するように、該物体の状態空間をセルに分割するセル作成部と、
該状態空間において、該物体の状態遷移に対応する探索木を、該物体の状態に対応する、該探索木の枝のノードがセルに一つずつ含まれるように作成する探索木作成部と、
該探索木を使用して、該物体の現在の状態から目標状態までの軌道を定める軌道作成部と、を備える軌道計画システム。
【請求項5】
請求項4に記載の軌道計画システムと、該軌道計画システムが定めた軌道を実現する軌道制御部とを備えた軌道計画・制御システム。
【請求項1】
軌道計画システムによって、物体の状態を目標状態へ制御するための軌道を求める軌道計画方法であって、
該物体の状態空間をセルに分割するセル作成部が、所定のセルの数に対して、離散化による近似誤差を最小化するように該状態空間をセルに分割するステップと、
探索木作成部が、該状態空間において、該物体の状態遷移に対応する探索木を、該物体の状態に対応する、該探索木の枝のノードがセルに一つずつ含まれるように作成するステップと、
軌道作成部が、該探索木を使用して、該物体の現在の状態から目標状態までの経路を定めるステップと、を含む、軌道計画方法。
【請求項2】
前記分割するステップにおいて、セルの近似誤差を、セル内に含まれる任意の点とセルの中心点に、入力を与えた場合の状態遷移先の距離の平均として表し、前記状態空間のセルの近似誤差の和が最小となるようにすることによって前記離散化による近似誤差を最小とする請求項1に記載の軌道計画方法。
【請求項3】
前記分割するステップが、前記状態空間を均一な基本セルに分割するステップと、前記所定のセルの数に達するまで、全ての基本セルを、セルの近似誤差を最も小さくする軸の方向に分割するステップと、セルの近似誤差の和を小さくするようにセルの分割と結合を繰り返すステップとを含む請求項1または2に記載の軌道計画方法。
【請求項4】
物体の状態を目標状態へ制御するための軌道を求める軌道計画システムであって、
離散化による近似誤差を最小化するように、該物体の状態空間をセルに分割するセル作成部と、
該状態空間において、該物体の状態遷移に対応する探索木を、該物体の状態に対応する、該探索木の枝のノードがセルに一つずつ含まれるように作成する探索木作成部と、
該探索木を使用して、該物体の現在の状態から目標状態までの軌道を定める軌道作成部と、を備える軌道計画システム。
【請求項5】
請求項4に記載の軌道計画システムと、該軌道計画システムが定めた軌道を実現する軌道制御部とを備えた軌道計画・制御システム。
【図1】


【図2】


【図3】


【図4】


【図5】


【図6】


【図7】


【図8】


【図9】


【図10】


【図11】


【図12】


【図13】


【図14】


【図15】




【図2】


【図3】


【図4】


【図5】


【図6】


【図7】


【図8】


【図9】


【図10】


【図11】


【図12】


【図13】


【図14】


【図15】


【公開番号】特開2012−234262(P2012−234262A)
【公開日】平成24年11月29日(2012.11.29)
【国際特許分類】
【出願番号】特願2011−100919(P2011−100919)
【出願日】平成23年4月28日(2011.4.28)
【出願人】(000005326)本田技研工業株式会社 (23,863)
【出願人】(899000068)学校法人早稲田大学 (602)
【Fターム(参考)】
【公開日】平成24年11月29日(2012.11.29)
【国際特許分類】
【出願日】平成23年4月28日(2011.4.28)
【出願人】(000005326)本田技研工業株式会社 (23,863)
【出願人】(899000068)学校法人早稲田大学 (602)
【Fターム(参考)】
[ Back to top ]

