カーネル主成分分析方法、カーネル主成分分析装置、カーネル主成分分析プログラム
【課題】計算量を削減することができ、かつ、計算量の削減に伴う計算精度の低下が従来よりも小さなカーネル主成分分析方法を実現する。
【解決手段】本発明の主成分分析方法は、n個の標本ベクトル{x1,x2,…,xn}からm個の標本ベクトル{y1,y2,…,ym}を選択する選択ステップと、一般化固有値問題KxyTKxyz=λKyzを解くことによって、r個の固有ベクトル{z1,z2,…,zr}を算出する設計ステップと、評価対象ベクトルxの特徴ベクトルy=[z1,z2,…,zr]TxΦを算出する評価ステップとを含んでいる。
【解決手段】本発明の主成分分析方法は、n個の標本ベクトル{x1,x2,…,xn}からm個の標本ベクトル{y1,y2,…,ym}を選択する選択ステップと、一般化固有値問題KxyTKxyz=λKyzを解くことによって、r個の固有ベクトル{z1,z2,…,zr}を算出する設計ステップと、評価対象ベクトルxの特徴ベクトルy=[z1,z2,…,zr]TxΦを算出する評価ステップとを含んでいる。
【発明の詳細な説明】
【技術分野】
【0001】
本発明は、主成分分析に関するものであり、特に、カーネル主成分分析に関するものである。
【背景技術】
【0002】
多変量解析のひとつとして、主成分分析(PCA:principal component analysis)がある。主成分分析は、n個の標本ベクトル{x1,x2,…,xn}(d次元ベクトル)に基づき、d次元の評価対象ベクトルxの特徴を表すr次元の特徴ベクトルyを算出する方法であり、(1)n個の標本ベクトル{x1,x2,…,xn}から定義される分散共分散行列の固有値問題を解き、r個の固有ベクトル{z1,z2,…,zr}を算出する設計ステップと、(2)r個の固有ベクトル{z1,z2,…,zr}を用いて評価対象ベクトルxを特徴ベクトルyに変換する評価ステップとにより構成することができる。得られる特徴ベクトルyの各成分は、評価対象ベクトルxの各主成分への射影を表し、「主成分得点」と称される。
【0003】
この主成分分析の拡張として、カーネル主成分分析(KPCA:Kernel principal component analysis)がある(非特許文献1参照)。カーネル主成分分析は、特徴空間と呼ばれる再生核ヒルベルト空間F上での主成分分析であり、例えば(1)n個の標本ベクトル{x1,x2,…,xn}から定義されるカーネルグラム行列Kxの固有値値問題を解き、r個の固有ベクトル固有ベクトル{z1,z2,…,zr}を算出する設計ステップと、(2)r個の固有ベクトル固有ベクトル{z1,z2,…,zr}を用いて評価対象ベクトルxを特徴ベクトルyに変換する評価ステップとにより構成することができる。ここで、カーネルグラム行列Kxとは、k(x、y)=<Φ(x)|Φ(y)>をMercerのカーネル関数として、カーネル関数値k(xi,xj)を第ij成分とするn×n行列のことである。Φ(x)は入力空間Rdから特徴空間Fへの写像を表し、<・|・>は内積を表す。
【0004】
カーネル主成分分析を用いることにより、非線形相関を考慮した多変量解析を行うことができる。しかしながら、n×n行列の固有値問題を解く必要があるため、計算量(計算の複雑さ)はn3に比例し、必要なメモリサイズはn2に比例する。したがって、現在のコンピュータの性能では、標本数nが数万から数十万を超えると、カーネル主成分分析を行うことが困難になる。このため、与えられたn個の標本ベクトル{x1,x2,…,xn}の一部のみを用いたカーネル主成分分析しか行えないことがしばしばであった。
【0005】
このような問題を考慮したカーネル主成分分析の改良としては、改良カーネル主成分分析(IKPCA:Improved Kernel principal component analysis)(非特許文献2参照)や、スパースカーネル主成分分析(非特許文献3、4)などが知られている。
【先行技術文献】
【非特許文献】
【0006】
【非特許文献1】B. Scholkopf and A. Smola and K.-R. Muller,“Nonlinear Component Analysis as a Kernel Eigenvalue Problem”,Neural computation,10,5,pp. 1299-1319,1998
【非特許文献2】Y. Xu, D. Zhang, F. Song, J. Yang, Z. Jing and M. Li,“Amethod for speeding up feature extraction based on KPCA”,Neurocomputing, pp. 1056-1061,2007
【非特許文献3】M. E. Tipping,“Sparse kernel principal component analysis”,Advances in Neural Information Processing Systems(NIPS),13,pp. 633-639,2001
【非特許文献4】A. J. Smola, O. L. Mgngasarian and B. Scholkopf,“Sparse kernel feature analysis”,Technical report 99-04,Universityof Wisconsin,1999
【発明の概要】
【発明が解決しようとする課題】
【0007】
しかしながら、上記従来の技術には、計算量を削減すると計算精度が大幅に低下するという問題があった。
【0008】
すなわち、与えられたn個の標本ベクトルの一部のみを用いてカーネル主成分分析を行えば、計算量も標本数の減少に応じて当然に減少する。しかし、用いる標本ベクトルの数を減らすと、得られる特徴ベクトルの精度低下を招来する。例えば、1000個の標本ベクトルが与えられたときに、50個の標本ベクトルを用いたカーネル主成分分析を行うと、得られる特徴ベクトルの精度が大幅に低下する。
【0009】
また、改良カーネル主成分分析は、適切な問題設定ではないため、近似が正確でないという問題を有している。また、スパースカーネル主成分分析は、評価ステップにおける計算量を削減することを目的とするものであり、設計ステップにおける計算量を削減することができないという問題を有している。
【0010】
本発明は、上記の問題に鑑みてなされたものであり、その目的は、計算量を削減することができ、かつ、計算量の削減に伴う計算精度の低下が従来よりも小さなカーネル主成分分析方法を実現することにある。
【課題を解決するための手段】
【0011】
本発明に係るカーネル主成分分析方法は、カーネル主成分分析装置を用いて、標本として与えられたn個のd次元ベクトル{x1,x2,…,xn}に基づき、評価対象として与えられたd次元ベクトルxの特徴を表現するr次元ベクトルyを算出するカーネル主成分分析方法である。上記課題を解決するために、本発明に係るカーネル主成分分析方法は、上記n個のd次元ベクトル{x1,x2,…,xn}からm個(mはn未満の自然数)のd次元ベクトル{y1,y2,…,ym}を選択する選択ステップ、又は、上記n個のd次元ベクトル{x1,x2,…,xn}とは別にm個のd次元ベクトル{y1,y2,…,ym}を取得する取得ステップと、カーネル関数値k(yi,yj)を第ij成分とするm×m行列をKyとし、カーネル関数値k(xi,yj)を第ij成分とするn×m行列をKxyとして、固有値λと固有ベクトルzを求める一般化固有値問題KxyTKxyz=λKyz、又は、正則化一般化固有値問題KxyTKxy(KxyTKxy+μKy)KxyTKxyz=λKyzを解くことによって、r個の固有ベクトル{z1,z2,…,zr}を算出する設計ステップと、上記r個の固有ベクトル{z1,z2,…,zr}を用いて、上記d次元ベクトルxを上記r次元ベクトルyに変換する評価ステップと、を含んでいる。ここで、k(x、y)=<Φ(x)|Φ(y)>は、従来のカーネル主成分分析に用いられているものと同じMercerのカーネル関数であり、μ>0は正則化パラメータである。
【0012】
上記の構成によれば、解くべき固有値問題はm×m行列(KxyTKxy及びKy)に関する一般化固有値問題になる(計算量m3)。このため、n個のd次元ベクトル{x1,x2,…,xn}を用いた従来のカーネル主成分分析方法(計算量n3)と比べて計算量を減少させることができる。しかも、本発明において解くべき一般化固有値問題には、(選択された)m個のd次元ベクトル{y1,y2,…,ym}に関する情報のみならず、(選択されたなかった)n−m個のd次元ベクトル{x1,x2,…,xn}\{y1,y2,…,ym}に関する情報がn×m行列Kxyを介して取り込まれている。したがって、(選択された)m個のd次元ベクトル{y1,y2,…,ym}のみを用いて従来のカーネル主成分分析を行う場合に比べて、より高い精度で特徴ベクトルyを算出することができる。したがって、計算量を削減することができ、かつ、計算量の削減に伴う計算精度の低下を従来よりも小さくすることができるという効果を奏する。
【0013】
なお、m個のd次元ベクトル{y1,y2,…,ym}を用いて従来のカーネル主成分分析を行う場合に比べて、より高い精度の特徴ベクトルyを算出することができることの、数学的な裏付けについては発明の詳細な説明の〔部分カーネル主成分分析の原理〕を、実験的な検証については発明の詳細な説明の〔数値実験による検証〕をそれぞれ参照されたい。
【0014】
なお、上記設計ステップは、例えば、(1)上記m個のd次元ベクトル{y1,y2,…,ym}から、上記m×m行列Kyを算出するステップと、(2)上記n個のd次元ベクトル{x1,x2,…,xn}、及び、上記m個のd次元ベクトル{y1,y2,…,ym}から、上記n×m行列Kxyを算出するステップと、(3)上記一般化固有値問題KxyTKxyz=λKyz、又は、KxyTKxy(KxyTKxy+μKy)KxyTKxyz=λKyzを解くことによって、上記r個の固有ベクトル{z1,z2,…,zr}を算出するステップとを含んで構成することができる。
【0015】
ただし、上記設計ステップは、カーネル関数値k(yi,yj)を第ij成分とするm×m行列をKyとし、カーネル関数値k(xi,yj)を第ij成分とするn×m行列をKxyとしたときに、KxyTKxyz=λKyzにより表現される一般化固有値問題、又は、KxyTKxy(KxyTKxy+μKy)KxyTKxyz=λKyzにより表現される正則化一般化固有値問題を解くことによって、r個の固有ベクトル{z1,z2,…,zr}を算出するものであれば何でもよく、必ずしも、上記m×m行列Ky自体、及び、上記n×m行列Kxy自体の算出を要するものではない。
【0016】
また、上記評価ステップは、例えば、(1)上記d次元ベクトルx、及び、上記m個のd次元ベクトル{y1,y2,…,ym}から、カーネル関数値k(x,yj)を第j成分とするm次元ベクトルxΦを算出するステップと、(2)上記r個の固有ベクトル{z1,z2,…,zr}、及び、上記m次元ベクトルxΦから、上記r次元ベクトルy=[z1,z2,…,zr]TxΦを算出するステップと、を含んで構成することができる。
【0017】
ただし、上記評価ステップは、カーネル関数値k(x,yj)を第j成分とするm次元ベクトルをxΦとし、上記r個の固有ベクトル{z1,z2,…,zr}を並べたm×r行列[z1,z2,…,zr]をZとしたときに、ZTxΦにより表現されるr次元ベクトルを算出するものであれば何でもよく、必ずしも、上記m次元ベクトルをxΦ自体、及び、上記m×r行列Z自体の算出を要するものではない。
【0018】
また、本発明に係るカーネル主成分分析方法は、上記評価ステップにて算出された上記r次元ベクトルyを他の装置に出力する出力ステップを含んでいてもよい。出力ステップにおける出力先となる装置は特に限定されるものではないが、例えば、上記r次元ベクトルyを表示装置(ディスプレイ等)、印刷装置(プリンタ等)、記録装置(光ディスクドライブ等)、送信装置(モデム等)を出力先とすることができる。表示装置/印刷装置を出力先とする場合には、上記r次元ベクトルyを数値列又はグラフとして表示又は印刷することができるし、記録装置を出力先とする場合には、上記r次元ベクトルyを記録媒体に記録することができるし、送信装置を出力先とする場合には、送信装置を介して上記r次元ベクトルyを他のコンピュータに送信することができる。これにより、ユーザが上記r次元ベクトルyを視覚的に認識したり、上記カーネル主成分分析装置または上記記録媒体から情報を読み出すことができる他装置が上記記録媒体から上記r次元ベクトルyを読み出して利用したり、他のコンピュータが上記送信装置から上記r次元ベクトルyを受信して利用したりすることができる。
【0019】
本発明に係るカーネル主成分分析方法において、上記選択ステップは、上記n個のd次元ベクトル{x1,x2,…,xn}をm個のクラスタ{C1,C2,…,Cm}にクラスタリングするステップと、上記m個のクラスタ{C1,C2,…,Cm}の各々から上記m個のd次元ベクトル{y1,y2,…,ym}の各々を選択するステップと、を含んでいる、ことが好ましい。
【0020】
上記構成によれば、m個のd次元ベクトル{y1,y2,…,ym}を選択するために要する計算量を徒に増加させることなく、特徴ベクトルyを精度良く計算することができるよう、m個のd次元ベクトル{y1,y2,…,ym}を選択することができる、という更なる効果を奏する。
【0021】
本発明に係るカーネル主成分分析方法は、上記選択ステップにおいて、上記n個のd次元ベクトル{x1,x2,…,xn}をm個のクラスタ{C1,C2,…,Cm}にクラスタリングする際に、特徴空間上のノルムを使用する、ことが好ましい。
【0022】
上記の構成によれば、特徴ベクトルyを更に精度良く計算することができるよう、m個のd次元ベクトル{y1,y2,…,ym}を選択することができる、という更なる効果を奏す。
【0023】
本発明に係るカーネル主成分分析方法において、上記ベクトルyの次元rは、上記ベクトルxの次元dよりも小さい、ことが好ましい。
【0024】
上記の構成によれば、伝送効率に優れたデータサイズの小さい特徴ベクトルyを得ることができる。例えば、本発明を情報源符号化に適用する場合、送信側(装置)と受信側(装置)とが上記m個のd次元ベクトル{y1,y2,…,ym}を予め共有することによって、送受信する情報量を削減することができる。
【0025】
本発明に係るカーネル主成分分析方法において、上記ベクトルyの次元rは、上記ベクトルxの次元dよりも大きい、ことが好ましい。
【0026】
上記の構成によれば、ノイズに強い冗長な特徴ベクトルyを得ることができる。例えば、本発明を通信路符号化に適用する場合、送信側(装置)と受信側(装置)とが上記m個のd次元ベクトル{y1,y2,…,ym}を予め共有することによって、雑音に対して頑健な情報を送受信することができる。
【0027】
本発明に係るカーネル主成分分析装置は、標本として与えられたn個のd次元ベクトル{x1,x2,…,xn}に基づき、評価対象として与えられたd次元ベクトルxの特徴を表現するr次元ベクトルyを算出するカーネル主成分分析装置である。そして、上記課題を解決するために、上記n個のd次元ベクトル{x1,x2,…,xn}からm個(mはn未満の自然数)のd次元ベクトル{y1,y2,…,ym}を選択する選択手段、又は、上記n個のd次元ベクトル{x1,x2,…,xn}とは別にm個のd次元ベクトル{y1,y2,…,ym}を取得する取得手段と、カーネル関数値k(yi,yj)を第ij成分とするm×m行列をKyとし、カーネル関数値k(xi,yj)を第ij成分とするn×m行列をKxyとして、一般化固有値問題KxyTKxyz=λKyz、又は、正則化一般化固有値問題KxyTKxy(KxyTKxy+μKy)KxyTKxyz=λKyzを解くことによって、r個の固有ベクトル{z1,z2,…,zr}を算出する設計手段と、上記d次元ベクトルxを上記r次元ベクトルyに変換する評価手段と、とを備えている。
【0028】
上記の構成によれば、上記カーネル主成分分析方法と同様、計算量を削減することができ、かつ、計算量の削減に伴う計算精度の低下を従来よりも小さくすることができるという効果を奏する。
【0029】
なお、本発明に係るカーネル主成分分析装置は、コンピュータによって実現してもよい。この場合、コンピュータを上記各手段として動作させることにより、上記カーネル主成分分析装置をコンピュータにおいて実現するプログラムも本発明の範疇に入る。
【0030】
また、本発明に係るカーネル主成分分析方法は、雑音除去方法、パターン分類方法、パターン検出方法、パターン分類方法、及び、欠損値補間方法に利用することができ、これらの方法の一部として利用されるカーネル主成分分析方法についても本発明の範疇に入る。
【発明の効果】
【0031】
本発明によれば、計算量を削減することができ、かつ、計算量の削減に伴う計算精度の低下を従来よりも小さくすることができるという効果を奏する。
【図面の簡単な説明】
【0032】
【図1】本発明の実施形態を示すものであり、部分カーネル主成分分析装置のブロック図である。
【図2】本発明の実施形態を示すものであり、部分カーネル主成分分析装置として機能するコンピュータのブロック図である。
【図3】本発明の実施形態を示すものであり、部分カーネル主成分分析方法のフローチャートである。
【図4】本発明の実施形態を示すものであり、部分カーネル主成分分析方法に含まれる選択ステップの構成例を示すフローチャートである。
【図5】本発明の実施形態を示すものであり、部分カーネル主成分分析方法に含まれる設計ステップの構成例を示すフローチャートである。
【図6】本発明の実施形態を示すものであり、部分カーネル主成分分析方法に含まれる評価ステップの構成例を示すフローチャートである。
【図7】人工データを用いた、本発明のカーネル主成分分析方法(部分カーネル主成分分析法)の計算精度と、従来のカーネル主成分分析方法の計算精度とを比較したグラフである。
【図8】実データを用いた、本発明のカーネル主成分分析方法(部分カーネル主成分分析法)の計算精度と、従来のカーネル主成分分析方法の計算精度とを比較したグラフである。
【図9】実データを用いた、本発明のカーネル主成分分析方法(部分カーネル主成分分析法)の計算精度と、従来のカーネル主成分分析方法の計算精度とを比較したグラフである。
【図10】実データを用いた、本発明のカーネル主成分分析方法(部分カーネル主成分分析法)の計算精度と、従来のカーネル主成分分析方法の計算精度とを比較したグラフである。
【図11】K−meansと無作為抽出との比較を示したグラフである。
【発明を実施するための形態】
【0033】
本発明に係るカーネル主成分分析方法は、発明者が見出した新規なカーネル主成分分析であり、部分カーネル主成分分析(SKPCA:Subset Kernel Principal Component Analysis)と呼ぶことにしたものである。そこで、本発明に係るカーネル主成分分析方法を、以下では、部分カーネル主成分分析方法と呼称する。また、本発明に係るカーネル主成分分析装置、すなわち、部分カーネル主成分分析を行う装置を、以下では、部分カーネル主成分分析装置と呼称する。
【0034】
〔実施形態〕
本発明の一実施形態について、図面に基づいて説明すれば以下のとおりである。
【0035】
(部分カーネル主成分分析装置)
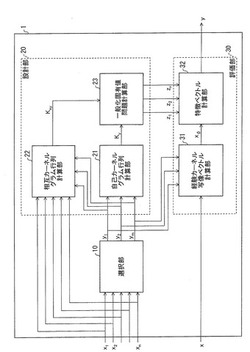
まず、部分カーネル主成分分析装置(以下、「SKPCA装置」と略記)について、図1を参照して説明する。図1は、本実施形態に係るSKPCA装置1の構成を示したブロック図である。SKPCA装置1は、図1に示したように、選択部10と、設計部20と、評価部30とを備えている。
【0036】
SKPCA装置1に入力される入力データは、標本として与えられたn個のd次元ベクトル{x1,x2,…,xn}と、評価対象として与えられたd次元ベクトルxとである。以下では、標本として与えられたn個のd次元ベクトル{x1,x2,…,xn}の各々を「標本ベクトル」と呼称し、評価対象として与えられたd次元ベクトルxを「評価対象ベクトル」と呼称する。一方、SKPCA装置1から出力される出力データは、評価対象ベクトルxの特徴を表現するr次元ベクトルyである。以下では、このr次元ベクトルyを「特徴ベクトル」と呼称する。
【0037】
選択部10は、入力されたn個の標本ベクトル{x1,x2,…,xn}からm個の標本ベクトル{y1,y2,…,ym}を選択するための手段である(mはn未満の自然数)。選択されたm個の標本ベクトル{y1,y2,…,ym}は、後述する自己カーネルグラム行列計算部21、相互カーネルグラム行列計算部22、及び、経験カーネル写像ベクトル計算部31がこれを参照することができるよう、不図示の記憶装置に格納される。選択部10により実行される選択処理の詳細については、参照する図面を代えて後述する。
【0038】
設計部20は、一般化固有値問題KxyTKxyz=λKyzを解くことによって、r個の固有ベクトル{z1,z2,…,zr}を算出するための手段であり、例えば、図1に示したように、自己カーネルグラム行列計算部21と、相互カーネルグラム行列計算部22と、一般化固有値問題計算部23とにより構成することができる。ここで、Kyは、カーネル関数値k(yi,yj)を第ij成分とするm×m行列であり、「自己カーネルグラム行列」と称される。また、Kxyは、カーネル関数値k(xi,yj)を第ij成分とするn×m行列であり、「相互カーネルグラム行列」と称される。
【0039】
設計部20を構成する各部が担う機能は、以下のとおりである。
【0040】
自己カーネルグラム行列計算部21は、選択部10により選択されたm個の標本ベクトル{y1,y2,…,ym}から、自己カーネルグラム行列Kyを計算するための手段である。より具体的に言うと、自己カーネルグラム行列計算部21は、選択された標本ベクトルyi及びyjを記憶装置から読み出し、これらを予め定められたカーネル関数k(x、y)に代入することによって、m×m行列である自己カーネルグラム行列Kyの第ij成分(Ky)ij=k(yi,yj)を算出する(i=1,2,…,m/j=1,2,…,m)。算出された自己カーネルグラム行列Kyは、後述する一般化固有値問題計算部23がこれを参照することができるよう、不図示の記憶装置に格納される。
【0041】
相互カーネルグラム行列計算部22は、入力されたn個の標本ベクトル{x1,x2,…,xn}と、選択部10により選択されたm個の標本ベクトル{y1,y2,…,ym}とから、相互カーネルグラム行列Kxyを算出するための手段である。より具体的に言うと、相互カーネルグラム行列計算部22は、入力された標本ベクトルxiと選択された標本ベクトルyjとを記憶装置から読み出し、これらをカーネル関数k(x,y)に代入することによって、n×m行列である相互カーネルグラム行列Kxyの第ij成分(Kxy)ij=k(xi,yj)を算出する(i=1,2,…,n/j=1,2,…,m)。算出された相互カーネルグラム行列Kxyは、後述する一般化固有値問題計算部23がこれを参照することができるよう、不図示の記憶装置に格納される。
【0042】
一般化固有値問題計算部23は、自己カーネルグラム行列計算部21により算出された自己カーネルグラム行列Kyと、相互カーネルグラム行列計算部22により算出された相互カーネルグラム行列Kxyとにより定義される一般化固有値問題KxyTKxyz=λKyzを解くことによって、r個の固有ベクトル{z1,z2,…,zr}を算出するための手段である。
【0043】
より具体的に言うと、一般化固有値問題計算部23は、(1)相互カーネルグラム行列Kxyの転置行列KxyTを算出し、(2)相互カーネルグラム行列Kxyとその転置行列KxyTとの行列積KxyTKxyを算出し、(3)一般化固有値問題KxyTKxyz=λKyzを解き、(4)得られた固有ベクトル(m次元の列ベクトル)のうち固有値の大きいものから順にr個の固有ベクトル{z1,z2,…,zr}を選択し、(5)選択したr個の固有ベクトル{z1,z2,…,zr}の各々を、ziTKyziのノルムが1になるように規格化する。規格化されたr個の固有ベクトル{z1,z2,…,zr}は、後述する特徴ベクトル計算部32がこれを参照することができるよう、不図示の記憶装置に格納される。
【0044】
なお、一般化固有値問題には公知の数値解法が幾つも存在しており、コンピュータ上で一般化固有値問題を解くためサブルーチンも広く利用されている。例えば、MATLAB(登録商標)に含まれているeigsやIntel Math Kernel Library(登録商標)に含まれているdsygvxなどは、その一例である。これらのサブルーチンを利用すれば、コンピュータを一般化固有値問題計算部23として機能させることができる。
【0045】
評価部30は、評価対象ベクトルxを特徴ベクトルy=ZTxΦに変換するための手段であり、例えば、図1に示したように、経験カーネル写像ベクトル計算部31と、特徴ベクトル計算部32とにより構成することができる。ここで、xΦは、カーネル関数値k(x,yj)を第j成分とするm次元ベクトルであり、「経験カーネル写像ベクトル」と称される。また、Zは、r個の固有ベクトル{z1,z2,…,zr}を並べたm×r行列[z1,z2,…,zr]である。
【0046】
評価部30を構成する各部が担う機能は、以下のとおりである。
【0047】
経験カーネル写像ベクトル計算部31は、入力された評価対象ベクトルxと、選択部10により選択されたm個の標本ベクトル{y1,y2,…,ym}とから、経験カーネル写像ベクトルxΦを算出するための手段である。より具体的に言うと、経験カーネル写像ベクトル計算部31は、入力された評価対象ベクトルxと選択された標本ベクトルyjとを記憶装置から読み出し、これらをカーネル関数k(x、y)に代入することによって、m次元の列ベクトルである経験カーネル写像ベクトルxΦの第j成分(xΦ)j=k(x,yj)を算出する(j=1,2,…,m)。算出された経験カーネル写像ベクトルxΦは、後述する特徴ベクトル計算部32がこれを参照することができるよう、不図示の記憶装置に格納される。
【0048】
特徴ベクトル計算部32は、一般化固有値問題計算部23により算出されたr個の固有ベクトル{z1,z2,…,zr}と、経験カーネル写像計算部21により算出された経験カーネル写像ベクトルxΦとから、特徴ベクトルy=ZTxΦを算出するための手段である。より具体的に言うと、特徴ベクトル計算部32は、規格化された固有ベクトルziと経験カーネル写像ベクトルxΦとを記憶装置から読み出し、これらの内積を算出することによって、r次元ベクトルである特徴ベクトルyの第i成分を算出する(i=1,2,…,r)。あるいは、行列ZTに経験カーネル写像ベクトルxΦを右から乗ずることによって、特徴ベクトルyを算出する。
【0049】
なお、算出する特徴ベクトルyの次元rは、入力される評価対象ベクトルxの次元dより高く設定されていてもよいし、低く設定されていてもよい。前者の場合、ノイズに強い冗長な特徴ベクトルyを得ることができ(冗長情報付加)、後者の場合、伝送効率に優れたデータサイズの小さい特徴ベクトルyを得ることができる(情報圧縮)。
【0050】
また、本実施形態においては、与えられたn個の標本ベクトル{x1,x2,…,xn}と、n個の標本ベクトル{x1,x2,…,xn}から選択されたm個の標本ベクトル{y1,y2,…,ym}とから算出された自己カーネルグラム行列Ky、相互カーネルグラム行列Kxy、及び、経験カーネル写像ベクトルxΦを用いて部分カーネル主成分分析を行う構成を示したが、本発明はこれに限定されるものではない。すなわち、後述する〔部分カーネル主成分分析の原理〕からも明らかなように、n個の標本ベクトル{x1,x2,…,xn}と、これとは別に与えられたm個の標本ベクトル{y1,y2,…,ym}とにより定義される自己カーネルグラム行列Ky、相互カーネルグラム行列Kxy、及び、経験カーネル写像ベクトルxΦを用いて部分カーネル主成分分析を行う構成を採用してもよい。この場合、自己カーネルグラム行列計算部21、相互カーネルグラム行列計算部22、及び、経験カーネル写像ベクトル計算部31が、n個の標本ベクトル{x1,x2,…,xn}と同様に、m個の標本ベクトル{y1,y2,…,ym}を直接外部から取得するようにすればよい。
【0051】
また、本実施形態においては、一般化固有値問題KxyTKxyz=λKyzを解くことによって、部分カーネル主成分分析を行う構成を示したが、本発明はこれに限定されるものではない。すなわち、一般化固有値問題KxyTKxyz=λKyzに代えて、正則化一般化固有値問題KxyTKxy(KxyTKxy+μKy)KxyTKxyz=λKyzを解くことによって、部分カーネル主成分分析を行う構成を採用してもよい。なお、正則化一般化固有値問題については、後述する〔部分カーネル主成分分析の原理〕を参照されたい。
【0052】
(カーネル主成分分析装置の構成例)
SKPCA装置1は、コンピュータ(電子計算機)を用いて構成することができる。図2は、SKPCA装置1として利用可能なコンピュータ100の構成を例示したブロック図である。
【0053】
コンピュータ100は、図2に示したように、バス110を介して互いに接続された演算装置120と、主記憶装置130と、補助記憶装置140と、入出力インタフェース150とを備えている。演算装置120として利用可能なデバイスとしては、CPU(Central Processing Unit)を挙げることができる。また、主記憶装置130として利用可能なデバイスとしては、例えば、半導体RAM(random access memory)を挙げることができる。また、補助記憶装置140として利用可能なデバイスとしては、例えば、ハードディスクドライブを挙げることができる。
【0054】
入出力インタフェース150には、図2に示したように、入力装置200及び出力装置300が接続される。ユーザにより指定された数値を入力データ(標本ベクトル及び評価対象ベクトル)とする場合には、例えば、キーボードを入力装置200として利用することができる。また、測定値を入力データとする場合には、例えば、その測定値に応じた測定器(センサ)を入力装置200として利用することもできる。また、出力データ(特徴ベクトル)を数値列又はグラフとしてユーザに提示する場合、例えば、モニタやプリンタなどを出力装置300として利用することができる。
【0055】
なお、出力装置300を介して出力データを出力する代わりに、記録媒体に出力データを記録するようにしてもよい。また、出力データを出力装置300に出力する代わりに、他の装置に出力データを送信するようにしてもよい。
【0056】
補助記憶装置140には、コンピュータ100をSKPCA装置1として動作させるためのカーネル主成分分析プログラム(以下「KPCAプログラム」と略記する)が格納されている。KPCAプログラムは、選択プログラムと、自己カーネルグラム行列計算プログラムと、相互カーネルグラム行列計算プログラムと、一般化固有値問題計算プログラムと、経験カーネル写像ベクトル計算プログラムと、特徴ベクトル計算プログラムとを含んでいる。
【0057】
演算装置120は、主記憶装置130上に展開された標本プログラムに含まれる命令を実行することによって、コンピュータ100を選択部10として機能させる。同様に、主記憶装置130上に展開された自己カーネルグラム行列計算プログラム、相互カーネルグラム行列計算プログラム、一般化固有値問題計算プログラム、経験カーネル写像ベクトル計算プログラム、及び、特徴ベクトル計算プログラムに含まれる命令を実行することによって、コンピュータ100を自己カーネルグラム行列計算部21、相互カーネルグラム行列計算部22、一般化固有値問題計算部23、経験カーネル写像ベクトル計算部31、及び、特徴ベクトル計算部32として機能させる。
【0058】
KPCAプログラムを実行する過程で生成される中間データ、すなわち、標本ベクトル{y1,y2,…,ym}、相互カーネルグラム行列Kxy、自己カーネルグラム行列Ky、相互カーネルグラム行列の転置行列KxyT、相互カーネルグラム行列Kxyとその転置行列KxyTとの行列積KxyTKxy、固有ベクトル{z1,z2,…,zr}、及び、経験カーネル写像ベクトルxΦは、演算装置120がこれを参照することができるよう主記憶装置130に格納される。ただし、主記憶装置130の記憶容量に制約がある場合には、これらの中間データを補助記憶装置140に格納するようにしてもよい。他のデータと比べてサイズの大きい相互カーネルグラム行列Kxyだけを補助記憶装置140に格納するような構成も有効である。
【0059】
(カーネル主成分分析方法)
次に、部分カーネル主成分分析方法(以下、「SKPCA方法」と略記する)について、図3〜図6を参照して説明する。
【0060】
図3は、本実施形態に係るSKPCA方法S1の流れを示したフローチャートである。SKPCA方法S1は、SKPCA装置1を用いたSKPCA方法であり、図3に示したように、選択ステップS10と、設計ステップS20と、評価ステップS30とを含んでいる。また、図3に示したように、標本ベクトル入力ステップSin1と、評価対象ベクトル入力ステップSin2と、特徴ベクトル出力ステップSoutとを更に含んでいる。
【0061】
標本ベクトル入力ステップSin1においては、SKPCA装置1が、n個の標本ベクトル{x1,x2,…,xn}の入力を受け付ける。換言すれば、n個の標本ベクトル{x1,x2,…,xn}を入力装置等の外部装置から取得する。
【0062】
選択ステップS10においては、SKPCA装置1の選択部10が、標本ベクトル入力ステップSin1にて入力されたn個の標本ベクトル{x1,x2,…,xn}からm個の標本ベクトル{y1,y2,…,ym}を選択する。
【0063】
設計ステップS20においては、SKPCA装置1の設計部20が、一般化固有値問題KxyTKxyz=λKyzを解くことによって、r個の固有ベクトル{z1,z2,…,zr}を算出する。自己カーネルグラム行列Ky、及び、相互カーネルグラム行列Kxyは、上述したとおり、標本ベクトル入力ステップSin1にて入力されたn個の標本ベクトル{x1,x2,…,xn}、及び、選択ステップS10にて選択されたm個の標本ベクトル{y1,y2,…,ym}に基づいて定義することができる行列である。
【0064】
評価対象ベクトル入力ステップSin2においては、SKPCA装置1が、評価対象ベクトルxの入力を受け付ける。換言すれば、評価対象ベクトルxを入力装置等の外部装置から取得する。なお、評価対象ベクトル入力ステップSin2は、評価ステップS30より前に実行されればよく、設計ステップS20より後に実行されることを要さない。すなわち、設計ステップS20より前に、あるいは、選択ステップS10より前に実行されてもよい。
【0065】
評価ステップS30においては、SKPCA装置1の評価部30が、設計ステップS20にて算出されたr個の固有ベクトル{z1,z2,…,zr}とを用いて、評価対象ベクトル入力ステップSin2にて入力された評価対象ベクトルxを特徴ベクトルy=ZTxΦに変換する。
【0066】
特徴ベクトル出力ステップSoutにおいては、SKPCA装置1が、評価ステップS30にて算出された特徴ベクトルyを出力する。例えば、モニタを用いて特徴ベクトルyを数値列又はグラフとして表示したり、プリンタを用いて特徴ベクトルyを数値又はグラフとして印刷したりする。なお、特徴ベクトルyを表示したり印刷したりする代わりに、特徴ベクトルyを記録媒体に記録したり他の装置に送信したりしてもよい。
【0067】
なお、特徴ベクトルyをグラフとして表示または印刷する場合、特徴ベクトルyの次元が1であれば直線上の点としてこれをプロットすることができるし、特徴ベクトルyの次元が2であれば平面上の点としてこれをプロットすることができるし、特徴ベクトルyの次元が3であれば、(仮想)3次元空間上の点としてこれをプロットすることができる。この場合、評価対象ベクトルxと合わせて表示すれば、評価対象ベクトルxと特徴ベクトルyとの関係も一目瞭然である。
【0068】
図4は、選択ステップS10の構成例を示したフローチャートである。選択ステップS10は、例えば図4に示したように、クラスタリングステップS11と、標本ベクトル選択ステップS12とにより構成することができる。
【0069】
クラスタリングステップS11においては、選択部10が、標本ベクトル入力ステップSin1にて入力されたn個の標本ベクトル{x1,x2,…,xn}をm個のクラスタ{C1,C2,…,Cm}にクラスタリングする。
【0070】
標本ベクトル選択ステップS12においては、選択部10が、クラスタリングステップS11にてクラスタリングされたm個のクラスタ{C1,C2,…,Cm}の各々からm個の標本ベクトル{y1,y2,…,ym}の各々を選択する。
【0071】
なお、クラスタリングステップS11においては、Φ(xi)が属する特徴空間Fにおける距離を用いたクラスタリングを行うことができる。これにより、標本ベクトルxiが属する空間Rdにおける距離を用いたクラスタリングを行う場合と比べて、より精度の高い特徴ベクトルを得ることができる。特徴空間Fにおける距離としては、例えば、‖Φ(xi)−Φ(xj)‖2=k(xi,xi)+k(xj,xj)−2k(xi,xj)が挙げられる。
【0072】
クラスタリングステップS11において利用可能な公知のクラスタリング手法としては、階層化クラスタリングやK-meansなどを挙げることができる。例えば、K-meansを利用した場合、(1)初期クラスタ重心{<C1>,<C2>,…,<Cm>}をn個の標本ベクトル{x1,x2,…,xn}から適当に選び出し、(2)各標本ベクトルxjを、特徴空間Fにおける距離‖Φ(xj)−<Ci>‖2が最小となるクラスタCiに割り振り、(3)各クラスタ重心<Ci>を、<Ci>=(1/|Ci|)Σx∈CiΦ(x)により更新する処理を、クラスタ重心{<C1>,<C2>,…,<Cm>}が更新されなくなるまで繰り返すことによって、n個の標本ベクトル{x1,x2,…,xn}をm個のクラスタ{C1,C2,…,Cm}にクラスタリングすることができる。
【0073】
また、標本ベクトル選択ステップS12においては、各クラスタCiに属する標本ベクトルのうち、特徴空間FにおいてクラスタCiの重心に最も近い標本ベクトル、すなわち、argminx∈Ci‖Φ(x)−<Ci>‖2を取り出し、これを標本ベクトルyiとすることが好ましい。あるいは、クラスタCiに属する標本ベクトルのうち、入力空間Rdにおいてクラスタ重心Ciに最も近い標本ベクトル(いわゆるPre-image)を取り出し、これを標本ベクトルyiとすることが好ましい。これにより、各クラスタから他の標本ベクトルを取り出す場合と比べて、より精度の高い特徴ベクトルを得ることができる。なお、Pre-imageについては、以下の文献を参照されたい。
【0074】
S. Mika, B. Scholkopf and A. Smola,“Kernel PCA and denoising in feature space”,Advances in neural information processing systems (NIPS),11,pp,536-542 (1999)。
【0075】
B. Scholkopf,S. Mika,C. Burges,P. Knirsch,K.-R. Muller,G. Ratsch and A. Smola,“Input space vs. feature space in kernel-based methods”,IEEE Transactions on Neural Networks,10,5,pp. 1000-1017 (1999)。
【0076】
M. Girolami,“Mercer kernel-based clustering in feature space”,IEEE trans. on neural networks,13,3,pp. 780-784(2002)。
【0077】
なお、選択ステップS10の構成は、図4に示したものに限らない。特に、SKPCA方法S1では近似誤差あるいは残差を容易に算出することができるので、前向き選択や後向き選択などの標本選択の手法を容易に導入することができる。更に、無作為抽出されたm個の標本ベクトル{y1,y2,…,ym}を用いたSKPCA方法S1を繰り返し、所望の精度を有する特徴ベクトルyを算出するような構成を採ることもできる。
【0078】
図5は、設計ステップS20の構成例を示したフローチャートである。設計ステップ20は、例えば図5に示したように、自己カーネルグラム行列計算ステップS21と、相互カーネルグラム行列計算ステップS22と、一般化固有値問題計算ステップS23とにより構成することができる。
【0079】
自己カーネルグラム行列計算ステップS21においては、評価部20の自己カーネルグラム行列計算部21が、選択ステップ10にて選択されたm個の標本ベクトル{y1,y2,…,ym}から、自己カーネルグラム行列Kyを算出する。
【0080】
相互カーネルグラム行列計算ステップS22においては、評価部20の相互カーネルグラム行列計算部22が、標本ベクトル入力ステップSin1にて入力されたn個の標本ベクトル{x1,x2,…,xn}と、選択ステップ10にて選択されたm個の標本ベクトル{y1,y2,…,ym}とから、相互カーネルグラム行列Kxyを算出する。
【0081】
一般化固有値問題計算ステップS23においては、評価部20の一般化固有値問題計算部23が、自己カーネルグラム行列計算ステップS21にて算出された自己カーネルグラム行列Kyと、相互カーネルグラム行列計算ステップS22にて算出された相互カーネルグラム行列Kxyとにより定義される一般化固有値問題KxyTKxyz=λKyzを解くことによって、r個の固有ベクトル{z1,z2,…,zr}を算出する。
【0082】
なお、自己カーネルグラム行列計算ステップS21及び相互カーネルグラム行列計算ステップS22は、一般化固有値問題計算ステップS23より以前に実行されればよく、これらの実行順序は図5に示したものに限定されない。すなわち、図5においては自己カーネルグラム行列計算ステップS21を実行した後で相互カーネルグラム行列計算ステップS22を実行するようにしているが、相互カーネルグラム行列計算ステップS22を実行した後で自己カーネルグラム行列計算ステップS21を実行するようにしてもよい。
【0083】
図6は、評価ステップS30の構成例を示したフローチャートである。評価ステップS30は、例えば図6に示したように、経験カーネル写像ベクトル計算ステップS31と、特徴ベクトル計算ステップS32と、により構成することができる。
【0084】
経験カーネル写像ベクトル計算ステップS31においては、評価部30の経験カーネル写像ベクトル計算部31が、評価対象ベクトル取得ステップSin2にて入力された評価対象ベクトルxと、選択ステップ10にて選択されたm個の標本ベクトル{y1,y2,…,ym}とから、経験カーネル写像ベクトルxΦを算出する。
【0085】
特徴ベクトル計算ステップS32においては、評価部30の特徴ベクトル計算部32が、一般化固有値問題計算ステップS23にて算出されたr個の固有ベクトル{z1,z2,…,zr}と、経験カーネル写像計算ステップS21にて算出された経験カーネル写像ベクトルxΦとから、特徴ベクトルyを算出する。
【0086】
〔部分カーネル主成分分析の応用〕
部分カーネル主成分分析は、カーネル主成分分析と同様、雑音除去、パターン分類、パターン検出、欠損値補完、統計的推定、統計的予測、脳コンピュータインタフェース(BCI)などに応用することができる。これらの問題に部分カーネル主成分分析を適用する仕方は、これらの問題に従来のカーネル主成分分析を適用する仕方と同様である。
【0087】
例えば、部分カーネル主成分分析を用いた雑音除去方法は、従来、カーネル主成分分析により得られた特徴ベクトルを用いて行われていた逆変換写像の計算を、部分カーネル主成分分析により得られた特徴ベクトルを用いて行うようにすることにより実現することができる。逆変換写像の計算に部分カーネル主成分分析を用いた場合、従来のカーネル主成分分析を用いた場合と比べて、少ない計算量で効率の良い雑音除去を行うことができる。
【0088】
パターン分類、パターン検出、及び、欠損値補間においては、例えば、以下のようにして部分主成分分析方法を用いることができる。
【0089】
パターン分類は、p個のクラス{A1,A2,…,Ap}に分類されているq個の標本ベクトル{s1,s2,…,sq}基づき、対象ベクトルtを分類すべきクラスを決定する方法である。(1)各クラスAiに分類されているni個の標本ベクトル{si1,si2,…,sini}に基づく部分カーネル主成分分析を実行することによって、対象ベクトルtの特徴ベクトルuiを各j=1,…,pについて算出し、(2)特徴ベクトルujのノルムが最大となるクラスAjに対象ベクトルtを分類すれば、少ない計算量で精度良くパターン分類を行うことができる。
【0090】
パターン検出は、或るパターンを有するq個の標本ベクトル{s1,s2,…,sq}に基づき、対象ベクトルtがそのパターンを有するか否かを判定する方法である。(1)
q個の標本ベクトル{s1,s2,…,sq}に基づく部分カーネル主成分分析を実行することによって、対象ベクトルtの特徴ベクトルuを算出し、(2)特徴ベクトルuのノルムを予め定められた閾値Thと比較することによって、対象ベクトルtが特定のパターンを有するか否かを判定すれば、少ない計算量で精度良くパターン検出を行うことができる。
【0091】
欠損値補完は、q個の標本ベクトル{s1,s2,…,sq}に基づき、第k成分に欠損のある対象ベクトルtに対する欠損値補完を行う方法である。(1)第k成分を異なる値に設定したp個の対象ベクトル{t1,t2,…,tp}の各々について、q個の標本ベクトル{x1,x2,…,xq}に基づく部分カーネル主成分分析を実行することによって、対象ベクトルtiの特徴ベクトルuiを算出し、(2)特徴ベクトルujのノルムが最大となる対象ベクトルtjの第k成分の値を欠損のある対象ベクトルtの第k成分の値とすれば、少ない計算量で精度良く欠損値補間を行うことができる。
【0092】
なお、与えられたベクトルデータを対象ベクトルtと看做し、与えられたベクトルデータにおける未知の値を対象ベクトルtにおける欠損成分と看做せば、対象ベクトルtの欠損値補完を行うことにより、ベクトルデータにおける未知の値を統計的に推定することができる(統計的推定)。また、時系列データを対象ベクトルtと看做し、時系列データにおける未来の値を対象ベクトルtにおける欠損成分と看做せば、対象ベクトルtの欠損値補完を行うことにより、時系列データにおける未来の値を統計的に予測することができる(統計的予測)。
【0093】
更に、部分カーネル主成分分析は、脳コンピュータインタフェース(BCI)に応用することができる。脳信号の測定には、脳電図(EEG)、脳磁図(MEG)、近赤外光トポグラフィー(NIRS)、fMRIなどが用いられるが、ここでは、EEGを用いたBCIについて説明する。
【0094】
EEGによって得られた脳信号は、通常、多チャンネルであり、かつ、雑音を多く含む。そこで、BCIの前処理として、アーチファクト除去、バンドパスフィルタ(BPF)、CSP(Common Spatial Patterns)などの処理が施される。その後、入力信号は適当な時間幅をもつ窓で区切られ、データは数値列で表される。この数値列を評価対象ベクトルxとして部分カーネル主成分分析を利用する。この際、標本ベクトル{x1,x2,…,xn}は予め与えておく。そして、部分カーネル主成分分析により得られた特徴ベクトルyを、識別器で判別することによって、BCIの結果を得る。
【0095】
〔部分カーネル主成分分析の原理〕
次に、本発明の基礎となる部分カーネル主成分分析の原理について説明する。
【0096】
1.カーネル主成分分析
本節では、簡略にKPCAについて示した後、Mercerカーネル(1)を用いたKPCAの特徴付けを行う。
【0097】
【数1】

【0098】
x1,x2,…,xnをd次元の標本とする。特徴空間Fへ変換された標本Φ(x1),…,Φ(xn)の相関作用素RFは、(2)で与えられる。
【0099】
【数2】

【0100】
ここで,ケット-ブラ表記|・><・|は|a><b|c=<c,b>aを満たす作用素である。有限次元では転置・Tを用いた表記abTと同値であるが、Gaussianカーネルなどを用いた場合は、Fが無限次元となるためケット-ブラ表記を用いる。RFの固有値分解を(3)とおく。
【0101】
【数3】

【0102】
ここで固有値λiは降順に並んでいるとする。r次元の固有空間への変換UKと射影作用素PKは、(4)(5)で与えられる。
【0103】
【数4】

【0104】
【数5】

【0105】
ここでeriは、Rrのi番目の標準基底(i番目の要素が1でそれ以外の要素が0のベクトル)を表す。
【0106】
通常,RFは非常に大きいか、無限次元から無限次元への作用素であるため固有値分解が難しい。そこで、以下の作用素Sを考える。
【0107】
【数6】

【0108】
Sの随伴作用素をS*と書くと、RF=(1/n)SS*の固有値、固有ベクトルは、Kx=S*S=nΣni=1λiviviT、ui=(1/√λi)Sviの関係を満たす。これより、(7)(8)が得られる。
【0109】
【数7】

【0110】
【数8】

【0111】
ここで、(Kx)ij=k(xi,xj)はカーネルグラム行列と呼ばれる。入力xに対して、以下の出力を得る。
【0112】
【数9】

【0113】
【数10】

【0114】
ここで、‖・‖はEuclidノルムまたはl2ノルムを表し、S*Φ(x)=[k(x,x1),…,k(x,xn)]Tは経験カーネル写像と呼ばれるn次元ベクトルである。
【0115】
以上の議論より、UKあるいはPKを求めるためには、n×nの大きさの対称行列の固有値分解が必要であり,経験カーネル写像S*Φ(x)を求めるためにはn回のカーネル関数の計算が必要となる。さらに入力xの評価のために、すべての標本を保存しておく必要がある。このため、nが大きくなると計算量、メモリ量が問題となることがある。特に標本数が数万から数十万を超えるような大規模な問題ではKPCAを適用することができない。
【0116】
KPCAを拡張するために,KPCAの特徴付けを行う。主成分分析は、ランク制約の下で近似誤差を最小とする行列と定義できる。
【0117】
【数11】

【0118】
ここで、Exは平均を表す。KPCAについても同様の特徴付けができる。
【0119】
【数12】

【0120】
ここで、N(A)はAの核空間、R(A)はAの値域あるいは像を表す。制約N(X)⊃R(S)⊥は特徴空間F中のSが張る空間以外についても考慮する必要があるため必要となる。入力次元空間の問題では、標本数が充分にあれば全空間を張ることが多いため、核空間や値域の議論を省略することが多い。しかしながら、高次元の特徴空間では、標本が全空間を張らないことが多いため、これらを正確に扱うことが重要である。本明細書においてもこれらを正確に扱う。
【0121】
2. 部分カーネル主成分分析
前節で示した通り、KPCAは特徴空間Fで、標本Φ(x1),…,Φ(xn)が張るRnと同型の空間上で問題が議論される。すなわち。標本Φ(x1),…,Φ(xn)は基底を成す。KPCAはすべての標本を基底に用いるため、固有値分解の大きさやカーネル関数の評価回数が大きい。そこで、基底を少数の標本に置き換えることにより、この問題を解決する。
【0122】
y1,…,ym(m<n)を基底のための標本とし、作用素(11)を考える。
【0123】
【数13】

【0124】
この基底の下で全標本を最良に低階数近似する作用素を部分カーネル主成分分析(SKPCA:SubsetKPCA)と定義する。
【0125】
[定義1](SubsetKPCA)以下の最適化問題の解を部分KPCAと呼ぶ。
【0126】
【数14】

【0127】
Ky=T*T、Kxy=S*Tとおき、A+で作用素または行列のMoore−Penrose一般逆、A1/2で自己共役作用素あるいは対称行列の平方根A1/2AT/2=Aを表す。A1/2は一般に対称ではなく、一意ではない。行列平方根やCholesky分解などを用いることができる。次にSKPCAの解を示す。
【0128】
[定理1](SKPCAの解)(Ky1/2)+KxyTKxy(KyT/2)+の固有値分解を(13)とおく。
【0129】
【数15】

【0130】
ここで、ξi (i=1,…,m)は降順に並んでいるものとする。W=[w1,…,wr]とおくと、最適化問題(12)の解の1つは、以下で与えられる。
【0131】
【数16】

【0132】
特にR(T)⊂R(S)であるような場合、すなわち{yi}mi=1が{xi}ni=1の部分集合で与えられるような場合、(14)で与えられる。
【0133】
【数17】

【0134】
証明は後述する。
【0135】
[系1]R(T)⊂R(S)ならばPSは正射影である。
【0136】
(証明)明らかにPS*=PSである。(Ky1/2)+Ky(KyT/2)+は、R(Ky)への正射影であり、R(Ky)⊃R(W)であることに注意すると、PSPS=T(KyT/2)+WWT(Ky1/2)+Ky(KyT/2)+WWT(Ky1/2)+T*=PSであり、PSは正射影である(証明終)。
【0137】
[系2]基底にx1,…,xnを用いるとSKPCAはKPCAに一致する。
【0138】
明らかであるため,証明は省略する。
【0139】
次にSKPCAに別の表現を与える。
【0140】
[補題1]A,BをR(A)⊂ R(B)を満たす非負定値の行列とする。このとき、(B1/2)+A(BT/2)+の固有値λ、と固有ベクトルvは、任意のスカラーαに関して、Au=λBu、u=α(BT/2)+vを満たす。さらに、(λ,u)がAu=λBuを満たすとき、任意のスカラーβに対して、(B1/2)+A(BT/2)+v=λv、v=βBT/2u を満たす。
【0141】
[命題1]補題より、R(T)⊂ R(S)ならば、一般固有値問題KxyTKxyz=λKyzの固有値の上位r個に対応する固有ベクトル{zi}ri=1を用いて、(15)と表される。
【0142】
【数18】

【0143】
ここで、Z=[z1…zr]であり、z1,…,zrは,<zi|Kyzi>=1,(i=1,…,r)となるように正規化されているとする。
【0144】
R(T)⊂R(S)ならば、SKPCAによるr次元への変換は、US=ZTT*で与えられ、入力をxとすると(16)である。
【0145】
【数19】

【0146】
以上の議論より、SKPCAは大きさmの(一般)固有値問題に帰着する。評価時についてもm回のカーネル関数の計算で評価でき,m個の標本を保存しておくだけでよい。これ以降、R(T)⊂R(S)である、すなわちy1,…,ymはx1,…,xnの部分集合で与えられているとする。
【0147】
IKPCAでは、変換作用素は、異なる考え方から導き出され、(17)で与えられている。
【0148】
【数20】

【0149】
非特許文献2ではIKPCAは識別のための特徴抽出に(18)の形で用いられている。
【0150】
【数21】

【0151】
すなわち、SKPCAと比較すると各次元の要素が(1/√ξi)倍されている。この影響は後段の識別性能にはあまり影響しないと考えられるが、機械学習のための特徴抽出以外の応用においては大きな誤差が生じる。
【0152】
3.正則化
標本数が少ないとき、統計的推定量はしばしば標本に過適合(overfit)することがある。特に高次元中で問題を解くカーネルトリックは自由度が高いため過適合しやすい。線形逆問題や回帰問題(リッジ回帰)などにおいては、過適合を防ぐために(Tikhonov)正則化がよく用いられる。そこで、本手法にも過適合を防ぐために正則化を導入する。
【0153】
正則化は、パラメータベクトルあるいは行列のノルムを最小化することにより実現される。SKPCAの正則化を正則化SKPCA(RSKPCA:RegularizedSKPCA)と呼び、以下に定義を示す。
【0154】
[定義2](正則化SKPCA)
【0155】
【数22】

【0156】
ここで、μ>0は正則化パラメータ、‖・‖FはFrobeniusノルムを表す。目的関数の第2項は適合の度合いを表し、正則化パラメータμが適合度合いと近似誤差のトレードオフの調整を行う。
【0157】
正則化SKPCAの解を示す。
【0158】
[定理2](正則化SKPCAの解)KxyTKxy+μKyが正則であるとき、正則化SKPCAの解の1つは、(20)で与えられる。
【0159】
【数23】

【0160】
ここで、qiは固有値分解(21)の固有ベクトルとして与えられる。
【0161】
【数24】

【0162】
ここで、固有値σiは降順に並んでいるものとする。KxyTKxy+μKyが特異の場合には、逆行列は一般逆行列に置き換わる。
【0163】
SKPCAと同様に、(KyT/2)+qiは、一般固有値問題KxyTKxy(KxyTKxy+μKy)-1KxyTKxyp=λKypで計算することができる。
【0164】
[命題2]R(T)⊂R(S)であるとき、KxyTKxy+μKyが正則となる必要十分条件は、N(T)={0}である。
【0165】
(証明)(i)必要条件を示す。KxyTKxyとKyは非負定値であるため、どちらかが正定値であれば,KxyTKxy+μKyは正則である。N(T)={0}であれば明らかにKyは正則である。(ii)十分条件を示す。正則であれば明らかに正定値であり、任意のx∈Rm,x≠0に対して<x|(KxyTKxy+μKy)x>=‖S*Tx‖2+μ‖Tx‖2が正であるため、N(T)={0}である(証明終)。
【0166】
[命題3]GaussianカーネルK(x,y)=exp(−c‖x−y‖2)を用いた場合、y1,…,ymが互いに異なる場合、Kyは正定値である。
【0167】
以上の命題より、KxyTKxy+μKyはGaussianカーネルを用いた場合は、標本が重複しなければ正則であり、また、多項式カーネルk(x,y)=<x,y+c>dの場合においても、dが充分に大きければKyは正則となる。
【0168】
正則化パラメータμは交差検定(cross validation)などにより実験的に決定出来る。教師なし学習として用いる場合は、学習用標本とは別に検定用標本z1,…,zlを用意し、その検定用標本の近似誤差Σli=1‖Φ(zi)−PRΦ(zi)‖2を最小化するようなμを探す。検定用標本と学習用標本を入れ替え、交差検定を行うことで最適な正則化パラメータが推定できる。
【0169】
〔数値実験による検証〕
次に、本発明の効果を検証するための数値実験について説明する。
【0170】
1.人工データによる実験
本実験においては、図7の(a)に示す2次元の1000個のデータを利用した。図7の(b)は、Gaussianカーネルk(x,y)=exp(−0.1‖x−y‖2)を用いたKPCAで5次元の部分空間への射影ノルムの等高線を表す。図7の(c)に、標本を無作為に50個選び出し、KPCAを行った結果を表す。簡便のため、これ以降、(b)のように標本すべてを用いたKPCAを全体KPCAと呼び、(c)のように標本の一部を使って求めたKPCAを縮減KPCAと呼ぶ。図7の(d)は縮減KPCAと同じ標本を基底に用いたSKPCA、図7の(e)は縮減KPCAと同じ標本を基底に用いたRSKPCA(μ=0.1)、図7の(f)はIKPCAを示す。
【0171】
定量的評価には2つの手法を用いた。1つ目の評価基準は、全標本に対する近似誤差(残差)である。
【0172】
【数25】

【0173】
Xは、PKやPSで置き換えられる。もう1つの評価基準は全体KPCAからの距離である。m次元中のr次元空間部分空間への正射影行列の全体の集合はGrassmann多様体(Grassmannian)と呼ばれ、その空間における距離の1つは射影行列の差のノルムで与えられる。KPCAとSKPCAも特徴空間F中のr次元部分空間への正射影作用素であるため、差のノルムで距離を定義する。ノルムにはFrobeniusノルムを用いた。全体KPCAの正射影作用素をPFKとおき、距離の2乗を全体KPCAのノルムの2乗‖PFK‖F2で割ったものを正規化距離Dとして定義する。
【0174】
【数26】

【0175】
図より、提案手法は全体KPCAとほとんど変わらない等高線を描くことが分かる。一方、縮減KPCAとIKPCAの等高線はKPCAから大きくかけ離れたものとなっている。近似誤差Eと正規化距離Dにおいても、提案手法は全体KPCAとほぼ変わらないのに対して、縮減KPCA、IKPCAはどちらも大きな値となっている。
【0176】
Intel Core2 Duo(登録商標) 2.16GHzを搭載したMacBook(登録商標)でMATLAB(登録商標)のIRAMを利用した固有値分解の関数eigsでは、1000×1000の対称行列の固有値分解で0.4秒、50×50の対称行列の固有値分解で0.02秒であった。この実験の場合では、提案法と縮減KPCAは、全体KPCAの場合より20倍高速に固有値分解を行うことができる。さらにカーネル関数の評価回数も20 分の1の回数で計算ができる。
【0177】
2.実データを用いた実験
UCI Machine learning repositoryにあるconcreteとhousingのデータセットを用いて実験を行った。concreteは9次元、1030個の標本があり、housingは14次元、506個の標本がある。カーネル関数にはGaussianカーネルを用い、パラメータcには、全要素の分散σ から、c=1/2σ2を求めて用いた。階数は入力次元と同じ次元で実験を行った。
【0178】
図8の(a)及び(b)は全体KPCAからの正規化距離を示す。IKPCAは、比較できない程度の大きな距離を示したため省略した。標本の部分集合は無作為抽出で行い、100回の無作為抽出の平均、標準偏差、最小値を示す。図より、標本数が全体の20%から10%程度であっても提案手法は全体KPCAから1%程度の誤差しか生じないことが確認できる。図9の(a)及び(b)は式(22)の誤差を全体KPCAの誤差で割った正規化誤差を示す。標本数が20%程度に減少した場合でも、正規化誤差の最小値は、全体KPCAの誤差の1.01倍程度であることが分かる。図10の(a)及び(b)は設計時の計算時間を示す。数値計算はIntel Math Kernel Library(登録商標)を用い、全体KPCA、縮減KPCAの固有値分解にはdsyevx、SKPCAの一般固有値分解には、dsygvxを用いた。図より、基底に用いる標本数が全標本数の70%以下の場合、提案手法の方が高速に設計を行うことができることがわかる。
【0179】
図11はhousingにおける無作為抽出と特徴空間中K‐meansによる標本選択の比較である。K‐meansの方が平均的によい近似性能を示し、標準偏差も小さいことが確認できる。
【0180】
最後に、正則化の効果を示すためにhousingの部分集合として100個(n=100)、基底にm個の標本を用いて、この部分集合に対する近似を最小にするSKPCA及び、正則化SKPCAを求め、それぞれの全体KPCAからの正規化距離を比較した。100回の試行における正規化距離の平均値を表1に示す。実験結果より、正則化を用いた方がよい近似を与えることが確認できた。
【0181】
【表1】

【0182】
〔定理の証明〕
[補題2]制約条件N(X)⊃R(T)⊥は、ある作用素A:Rm→Fを用いて、X=AT*と表されることと同値である。
【0183】
【数27】

【0184】
(証明)(i)<=はR(T)⊥=N(T)⊂N(X)より明らかである。(ii)⇒の方向、すなわち、「N(X)⊃R(T)⊥のときX=AT*となるAが存在する。」を示す。A=X(T*)+とおけばAT*=X(T*)+T*=XPR(T)=X(I−PR(T)⊥)である。ここで、Pχはχへの正射影を表す。N(X)⊃R(T)⊥より、XPR(T)⊥=0であり、AT*=Xとなる。(i),(ii)より補題を得る(証明終)。
【0185】
[補題3]制約条件R(X)⊂R(T)⊥は、ある作用素A:F→Rmを用いて、X=TAと表されることと同値である。
【0186】
証明は、補題2と同様なので省略する。
【0187】
定理2でμ=0とおけば定理1となるため、μ≧0として定理2のみを証明する。補題2,3よりX=TAT*とおける。作用素Aに対するトレースを任意の正規直交基底ui,i=1,…を用いてTrace(A)=Σi<ui|Aui>と定義する。最適化問題(19)の目的関数をJとおくと以下のとおりである。
【0188】
【数28】

【0189】
R(KxyT)=R(T*S)⊂R(T*)=R(Ky)より、KxyT=PR(Ky)KxyT=KyKy+KxyTであり、Kxy=Kxy(KyT/2)+KyT/2である。また、R(KxyTKxy+μKy)⊃R(KxyT)より、PR(KxyTKxy+μKy)KxyT=(KxyTKxy+μKy)1/2((KxyTKxy+μKy)1/2)+KxyT=KxyTである。これより、以下のようになる。
【0190】
【数29】

【0191】
ここでCはAに対する定数項を表す。式(21) の固有値分解より、特異値分解を以下のように置く。
【0192】
【数30】

【0193】
Schmidtの近似定理(Eckart−Youngの定理)より、以下を満たすAが存在するときは、上式を満たすAがJを最小化する。
【0194】
【数31】

【0195】
【数32】

【0196】
以上より、式(A.1)を満たすAが存在し、その解の一つは、以下で与えられる。
【0197】
【数33】

【0198】
証明終
【産業上の利用可能性】
【0199】
本発明は、カーネル主成分分析を用いたデータ解析一般に広く適用することができる。特徴抽出、雑音除去、パターン分類、パターン検出、欠損値補完、統計的推定、統計的予測などに好適に利用することができる。
【符号の説明】
【0200】
1 SKPCA装置(カーネル主成分分析装置)
10 選択部(選択手段)
20 設計部(設計手段)
21 自己カーネルグラム行列計算部
22 相互カーネルグラム行列計算部
23 一般化固有値問題計算部
30 評価部(評価手段)
31 経験カーネル写像ベクトル計算部
32 特徴ベクトル計算部
【技術分野】
【0001】
本発明は、主成分分析に関するものであり、特に、カーネル主成分分析に関するものである。
【背景技術】
【0002】
多変量解析のひとつとして、主成分分析(PCA:principal component analysis)がある。主成分分析は、n個の標本ベクトル{x1,x2,…,xn}(d次元ベクトル)に基づき、d次元の評価対象ベクトルxの特徴を表すr次元の特徴ベクトルyを算出する方法であり、(1)n個の標本ベクトル{x1,x2,…,xn}から定義される分散共分散行列の固有値問題を解き、r個の固有ベクトル{z1,z2,…,zr}を算出する設計ステップと、(2)r個の固有ベクトル{z1,z2,…,zr}を用いて評価対象ベクトルxを特徴ベクトルyに変換する評価ステップとにより構成することができる。得られる特徴ベクトルyの各成分は、評価対象ベクトルxの各主成分への射影を表し、「主成分得点」と称される。
【0003】
この主成分分析の拡張として、カーネル主成分分析(KPCA:Kernel principal component analysis)がある(非特許文献1参照)。カーネル主成分分析は、特徴空間と呼ばれる再生核ヒルベルト空間F上での主成分分析であり、例えば(1)n個の標本ベクトル{x1,x2,…,xn}から定義されるカーネルグラム行列Kxの固有値値問題を解き、r個の固有ベクトル固有ベクトル{z1,z2,…,zr}を算出する設計ステップと、(2)r個の固有ベクトル固有ベクトル{z1,z2,…,zr}を用いて評価対象ベクトルxを特徴ベクトルyに変換する評価ステップとにより構成することができる。ここで、カーネルグラム行列Kxとは、k(x、y)=<Φ(x)|Φ(y)>をMercerのカーネル関数として、カーネル関数値k(xi,xj)を第ij成分とするn×n行列のことである。Φ(x)は入力空間Rdから特徴空間Fへの写像を表し、<・|・>は内積を表す。
【0004】
カーネル主成分分析を用いることにより、非線形相関を考慮した多変量解析を行うことができる。しかしながら、n×n行列の固有値問題を解く必要があるため、計算量(計算の複雑さ)はn3に比例し、必要なメモリサイズはn2に比例する。したがって、現在のコンピュータの性能では、標本数nが数万から数十万を超えると、カーネル主成分分析を行うことが困難になる。このため、与えられたn個の標本ベクトル{x1,x2,…,xn}の一部のみを用いたカーネル主成分分析しか行えないことがしばしばであった。
【0005】
このような問題を考慮したカーネル主成分分析の改良としては、改良カーネル主成分分析(IKPCA:Improved Kernel principal component analysis)(非特許文献2参照)や、スパースカーネル主成分分析(非特許文献3、4)などが知られている。
【先行技術文献】
【非特許文献】
【0006】
【非特許文献1】B. Scholkopf and A. Smola and K.-R. Muller,“Nonlinear Component Analysis as a Kernel Eigenvalue Problem”,Neural computation,10,5,pp. 1299-1319,1998
【非特許文献2】Y. Xu, D. Zhang, F. Song, J. Yang, Z. Jing and M. Li,“Amethod for speeding up feature extraction based on KPCA”,Neurocomputing, pp. 1056-1061,2007
【非特許文献3】M. E. Tipping,“Sparse kernel principal component analysis”,Advances in Neural Information Processing Systems(NIPS),13,pp. 633-639,2001
【非特許文献4】A. J. Smola, O. L. Mgngasarian and B. Scholkopf,“Sparse kernel feature analysis”,Technical report 99-04,Universityof Wisconsin,1999
【発明の概要】
【発明が解決しようとする課題】
【0007】
しかしながら、上記従来の技術には、計算量を削減すると計算精度が大幅に低下するという問題があった。
【0008】
すなわち、与えられたn個の標本ベクトルの一部のみを用いてカーネル主成分分析を行えば、計算量も標本数の減少に応じて当然に減少する。しかし、用いる標本ベクトルの数を減らすと、得られる特徴ベクトルの精度低下を招来する。例えば、1000個の標本ベクトルが与えられたときに、50個の標本ベクトルを用いたカーネル主成分分析を行うと、得られる特徴ベクトルの精度が大幅に低下する。
【0009】
また、改良カーネル主成分分析は、適切な問題設定ではないため、近似が正確でないという問題を有している。また、スパースカーネル主成分分析は、評価ステップにおける計算量を削減することを目的とするものであり、設計ステップにおける計算量を削減することができないという問題を有している。
【0010】
本発明は、上記の問題に鑑みてなされたものであり、その目的は、計算量を削減することができ、かつ、計算量の削減に伴う計算精度の低下が従来よりも小さなカーネル主成分分析方法を実現することにある。
【課題を解決するための手段】
【0011】
本発明に係るカーネル主成分分析方法は、カーネル主成分分析装置を用いて、標本として与えられたn個のd次元ベクトル{x1,x2,…,xn}に基づき、評価対象として与えられたd次元ベクトルxの特徴を表現するr次元ベクトルyを算出するカーネル主成分分析方法である。上記課題を解決するために、本発明に係るカーネル主成分分析方法は、上記n個のd次元ベクトル{x1,x2,…,xn}からm個(mはn未満の自然数)のd次元ベクトル{y1,y2,…,ym}を選択する選択ステップ、又は、上記n個のd次元ベクトル{x1,x2,…,xn}とは別にm個のd次元ベクトル{y1,y2,…,ym}を取得する取得ステップと、カーネル関数値k(yi,yj)を第ij成分とするm×m行列をKyとし、カーネル関数値k(xi,yj)を第ij成分とするn×m行列をKxyとして、固有値λと固有ベクトルzを求める一般化固有値問題KxyTKxyz=λKyz、又は、正則化一般化固有値問題KxyTKxy(KxyTKxy+μKy)KxyTKxyz=λKyzを解くことによって、r個の固有ベクトル{z1,z2,…,zr}を算出する設計ステップと、上記r個の固有ベクトル{z1,z2,…,zr}を用いて、上記d次元ベクトルxを上記r次元ベクトルyに変換する評価ステップと、を含んでいる。ここで、k(x、y)=<Φ(x)|Φ(y)>は、従来のカーネル主成分分析に用いられているものと同じMercerのカーネル関数であり、μ>0は正則化パラメータである。
【0012】
上記の構成によれば、解くべき固有値問題はm×m行列(KxyTKxy及びKy)に関する一般化固有値問題になる(計算量m3)。このため、n個のd次元ベクトル{x1,x2,…,xn}を用いた従来のカーネル主成分分析方法(計算量n3)と比べて計算量を減少させることができる。しかも、本発明において解くべき一般化固有値問題には、(選択された)m個のd次元ベクトル{y1,y2,…,ym}に関する情報のみならず、(選択されたなかった)n−m個のd次元ベクトル{x1,x2,…,xn}\{y1,y2,…,ym}に関する情報がn×m行列Kxyを介して取り込まれている。したがって、(選択された)m個のd次元ベクトル{y1,y2,…,ym}のみを用いて従来のカーネル主成分分析を行う場合に比べて、より高い精度で特徴ベクトルyを算出することができる。したがって、計算量を削減することができ、かつ、計算量の削減に伴う計算精度の低下を従来よりも小さくすることができるという効果を奏する。
【0013】
なお、m個のd次元ベクトル{y1,y2,…,ym}を用いて従来のカーネル主成分分析を行う場合に比べて、より高い精度の特徴ベクトルyを算出することができることの、数学的な裏付けについては発明の詳細な説明の〔部分カーネル主成分分析の原理〕を、実験的な検証については発明の詳細な説明の〔数値実験による検証〕をそれぞれ参照されたい。
【0014】
なお、上記設計ステップは、例えば、(1)上記m個のd次元ベクトル{y1,y2,…,ym}から、上記m×m行列Kyを算出するステップと、(2)上記n個のd次元ベクトル{x1,x2,…,xn}、及び、上記m個のd次元ベクトル{y1,y2,…,ym}から、上記n×m行列Kxyを算出するステップと、(3)上記一般化固有値問題KxyTKxyz=λKyz、又は、KxyTKxy(KxyTKxy+μKy)KxyTKxyz=λKyzを解くことによって、上記r個の固有ベクトル{z1,z2,…,zr}を算出するステップとを含んで構成することができる。
【0015】
ただし、上記設計ステップは、カーネル関数値k(yi,yj)を第ij成分とするm×m行列をKyとし、カーネル関数値k(xi,yj)を第ij成分とするn×m行列をKxyとしたときに、KxyTKxyz=λKyzにより表現される一般化固有値問題、又は、KxyTKxy(KxyTKxy+μKy)KxyTKxyz=λKyzにより表現される正則化一般化固有値問題を解くことによって、r個の固有ベクトル{z1,z2,…,zr}を算出するものであれば何でもよく、必ずしも、上記m×m行列Ky自体、及び、上記n×m行列Kxy自体の算出を要するものではない。
【0016】
また、上記評価ステップは、例えば、(1)上記d次元ベクトルx、及び、上記m個のd次元ベクトル{y1,y2,…,ym}から、カーネル関数値k(x,yj)を第j成分とするm次元ベクトルxΦを算出するステップと、(2)上記r個の固有ベクトル{z1,z2,…,zr}、及び、上記m次元ベクトルxΦから、上記r次元ベクトルy=[z1,z2,…,zr]TxΦを算出するステップと、を含んで構成することができる。
【0017】
ただし、上記評価ステップは、カーネル関数値k(x,yj)を第j成分とするm次元ベクトルをxΦとし、上記r個の固有ベクトル{z1,z2,…,zr}を並べたm×r行列[z1,z2,…,zr]をZとしたときに、ZTxΦにより表現されるr次元ベクトルを算出するものであれば何でもよく、必ずしも、上記m次元ベクトルをxΦ自体、及び、上記m×r行列Z自体の算出を要するものではない。
【0018】
また、本発明に係るカーネル主成分分析方法は、上記評価ステップにて算出された上記r次元ベクトルyを他の装置に出力する出力ステップを含んでいてもよい。出力ステップにおける出力先となる装置は特に限定されるものではないが、例えば、上記r次元ベクトルyを表示装置(ディスプレイ等)、印刷装置(プリンタ等)、記録装置(光ディスクドライブ等)、送信装置(モデム等)を出力先とすることができる。表示装置/印刷装置を出力先とする場合には、上記r次元ベクトルyを数値列又はグラフとして表示又は印刷することができるし、記録装置を出力先とする場合には、上記r次元ベクトルyを記録媒体に記録することができるし、送信装置を出力先とする場合には、送信装置を介して上記r次元ベクトルyを他のコンピュータに送信することができる。これにより、ユーザが上記r次元ベクトルyを視覚的に認識したり、上記カーネル主成分分析装置または上記記録媒体から情報を読み出すことができる他装置が上記記録媒体から上記r次元ベクトルyを読み出して利用したり、他のコンピュータが上記送信装置から上記r次元ベクトルyを受信して利用したりすることができる。
【0019】
本発明に係るカーネル主成分分析方法において、上記選択ステップは、上記n個のd次元ベクトル{x1,x2,…,xn}をm個のクラスタ{C1,C2,…,Cm}にクラスタリングするステップと、上記m個のクラスタ{C1,C2,…,Cm}の各々から上記m個のd次元ベクトル{y1,y2,…,ym}の各々を選択するステップと、を含んでいる、ことが好ましい。
【0020】
上記構成によれば、m個のd次元ベクトル{y1,y2,…,ym}を選択するために要する計算量を徒に増加させることなく、特徴ベクトルyを精度良く計算することができるよう、m個のd次元ベクトル{y1,y2,…,ym}を選択することができる、という更なる効果を奏する。
【0021】
本発明に係るカーネル主成分分析方法は、上記選択ステップにおいて、上記n個のd次元ベクトル{x1,x2,…,xn}をm個のクラスタ{C1,C2,…,Cm}にクラスタリングする際に、特徴空間上のノルムを使用する、ことが好ましい。
【0022】
上記の構成によれば、特徴ベクトルyを更に精度良く計算することができるよう、m個のd次元ベクトル{y1,y2,…,ym}を選択することができる、という更なる効果を奏す。
【0023】
本発明に係るカーネル主成分分析方法において、上記ベクトルyの次元rは、上記ベクトルxの次元dよりも小さい、ことが好ましい。
【0024】
上記の構成によれば、伝送効率に優れたデータサイズの小さい特徴ベクトルyを得ることができる。例えば、本発明を情報源符号化に適用する場合、送信側(装置)と受信側(装置)とが上記m個のd次元ベクトル{y1,y2,…,ym}を予め共有することによって、送受信する情報量を削減することができる。
【0025】
本発明に係るカーネル主成分分析方法において、上記ベクトルyの次元rは、上記ベクトルxの次元dよりも大きい、ことが好ましい。
【0026】
上記の構成によれば、ノイズに強い冗長な特徴ベクトルyを得ることができる。例えば、本発明を通信路符号化に適用する場合、送信側(装置)と受信側(装置)とが上記m個のd次元ベクトル{y1,y2,…,ym}を予め共有することによって、雑音に対して頑健な情報を送受信することができる。
【0027】
本発明に係るカーネル主成分分析装置は、標本として与えられたn個のd次元ベクトル{x1,x2,…,xn}に基づき、評価対象として与えられたd次元ベクトルxの特徴を表現するr次元ベクトルyを算出するカーネル主成分分析装置である。そして、上記課題を解決するために、上記n個のd次元ベクトル{x1,x2,…,xn}からm個(mはn未満の自然数)のd次元ベクトル{y1,y2,…,ym}を選択する選択手段、又は、上記n個のd次元ベクトル{x1,x2,…,xn}とは別にm個のd次元ベクトル{y1,y2,…,ym}を取得する取得手段と、カーネル関数値k(yi,yj)を第ij成分とするm×m行列をKyとし、カーネル関数値k(xi,yj)を第ij成分とするn×m行列をKxyとして、一般化固有値問題KxyTKxyz=λKyz、又は、正則化一般化固有値問題KxyTKxy(KxyTKxy+μKy)KxyTKxyz=λKyzを解くことによって、r個の固有ベクトル{z1,z2,…,zr}を算出する設計手段と、上記d次元ベクトルxを上記r次元ベクトルyに変換する評価手段と、とを備えている。
【0028】
上記の構成によれば、上記カーネル主成分分析方法と同様、計算量を削減することができ、かつ、計算量の削減に伴う計算精度の低下を従来よりも小さくすることができるという効果を奏する。
【0029】
なお、本発明に係るカーネル主成分分析装置は、コンピュータによって実現してもよい。この場合、コンピュータを上記各手段として動作させることにより、上記カーネル主成分分析装置をコンピュータにおいて実現するプログラムも本発明の範疇に入る。
【0030】
また、本発明に係るカーネル主成分分析方法は、雑音除去方法、パターン分類方法、パターン検出方法、パターン分類方法、及び、欠損値補間方法に利用することができ、これらの方法の一部として利用されるカーネル主成分分析方法についても本発明の範疇に入る。
【発明の効果】
【0031】
本発明によれば、計算量を削減することができ、かつ、計算量の削減に伴う計算精度の低下を従来よりも小さくすることができるという効果を奏する。
【図面の簡単な説明】
【0032】
【図1】本発明の実施形態を示すものであり、部分カーネル主成分分析装置のブロック図である。
【図2】本発明の実施形態を示すものであり、部分カーネル主成分分析装置として機能するコンピュータのブロック図である。
【図3】本発明の実施形態を示すものであり、部分カーネル主成分分析方法のフローチャートである。
【図4】本発明の実施形態を示すものであり、部分カーネル主成分分析方法に含まれる選択ステップの構成例を示すフローチャートである。
【図5】本発明の実施形態を示すものであり、部分カーネル主成分分析方法に含まれる設計ステップの構成例を示すフローチャートである。
【図6】本発明の実施形態を示すものであり、部分カーネル主成分分析方法に含まれる評価ステップの構成例を示すフローチャートである。
【図7】人工データを用いた、本発明のカーネル主成分分析方法(部分カーネル主成分分析法)の計算精度と、従来のカーネル主成分分析方法の計算精度とを比較したグラフである。
【図8】実データを用いた、本発明のカーネル主成分分析方法(部分カーネル主成分分析法)の計算精度と、従来のカーネル主成分分析方法の計算精度とを比較したグラフである。
【図9】実データを用いた、本発明のカーネル主成分分析方法(部分カーネル主成分分析法)の計算精度と、従来のカーネル主成分分析方法の計算精度とを比較したグラフである。
【図10】実データを用いた、本発明のカーネル主成分分析方法(部分カーネル主成分分析法)の計算精度と、従来のカーネル主成分分析方法の計算精度とを比較したグラフである。
【図11】K−meansと無作為抽出との比較を示したグラフである。
【発明を実施するための形態】
【0033】
本発明に係るカーネル主成分分析方法は、発明者が見出した新規なカーネル主成分分析であり、部分カーネル主成分分析(SKPCA:Subset Kernel Principal Component Analysis)と呼ぶことにしたものである。そこで、本発明に係るカーネル主成分分析方法を、以下では、部分カーネル主成分分析方法と呼称する。また、本発明に係るカーネル主成分分析装置、すなわち、部分カーネル主成分分析を行う装置を、以下では、部分カーネル主成分分析装置と呼称する。
【0034】
〔実施形態〕
本発明の一実施形態について、図面に基づいて説明すれば以下のとおりである。
【0035】
(部分カーネル主成分分析装置)
まず、部分カーネル主成分分析装置(以下、「SKPCA装置」と略記)について、図1を参照して説明する。図1は、本実施形態に係るSKPCA装置1の構成を示したブロック図である。SKPCA装置1は、図1に示したように、選択部10と、設計部20と、評価部30とを備えている。
【0036】
SKPCA装置1に入力される入力データは、標本として与えられたn個のd次元ベクトル{x1,x2,…,xn}と、評価対象として与えられたd次元ベクトルxとである。以下では、標本として与えられたn個のd次元ベクトル{x1,x2,…,xn}の各々を「標本ベクトル」と呼称し、評価対象として与えられたd次元ベクトルxを「評価対象ベクトル」と呼称する。一方、SKPCA装置1から出力される出力データは、評価対象ベクトルxの特徴を表現するr次元ベクトルyである。以下では、このr次元ベクトルyを「特徴ベクトル」と呼称する。
【0037】
選択部10は、入力されたn個の標本ベクトル{x1,x2,…,xn}からm個の標本ベクトル{y1,y2,…,ym}を選択するための手段である(mはn未満の自然数)。選択されたm個の標本ベクトル{y1,y2,…,ym}は、後述する自己カーネルグラム行列計算部21、相互カーネルグラム行列計算部22、及び、経験カーネル写像ベクトル計算部31がこれを参照することができるよう、不図示の記憶装置に格納される。選択部10により実行される選択処理の詳細については、参照する図面を代えて後述する。
【0038】
設計部20は、一般化固有値問題KxyTKxyz=λKyzを解くことによって、r個の固有ベクトル{z1,z2,…,zr}を算出するための手段であり、例えば、図1に示したように、自己カーネルグラム行列計算部21と、相互カーネルグラム行列計算部22と、一般化固有値問題計算部23とにより構成することができる。ここで、Kyは、カーネル関数値k(yi,yj)を第ij成分とするm×m行列であり、「自己カーネルグラム行列」と称される。また、Kxyは、カーネル関数値k(xi,yj)を第ij成分とするn×m行列であり、「相互カーネルグラム行列」と称される。
【0039】
設計部20を構成する各部が担う機能は、以下のとおりである。
【0040】
自己カーネルグラム行列計算部21は、選択部10により選択されたm個の標本ベクトル{y1,y2,…,ym}から、自己カーネルグラム行列Kyを計算するための手段である。より具体的に言うと、自己カーネルグラム行列計算部21は、選択された標本ベクトルyi及びyjを記憶装置から読み出し、これらを予め定められたカーネル関数k(x、y)に代入することによって、m×m行列である自己カーネルグラム行列Kyの第ij成分(Ky)ij=k(yi,yj)を算出する(i=1,2,…,m/j=1,2,…,m)。算出された自己カーネルグラム行列Kyは、後述する一般化固有値問題計算部23がこれを参照することができるよう、不図示の記憶装置に格納される。
【0041】
相互カーネルグラム行列計算部22は、入力されたn個の標本ベクトル{x1,x2,…,xn}と、選択部10により選択されたm個の標本ベクトル{y1,y2,…,ym}とから、相互カーネルグラム行列Kxyを算出するための手段である。より具体的に言うと、相互カーネルグラム行列計算部22は、入力された標本ベクトルxiと選択された標本ベクトルyjとを記憶装置から読み出し、これらをカーネル関数k(x,y)に代入することによって、n×m行列である相互カーネルグラム行列Kxyの第ij成分(Kxy)ij=k(xi,yj)を算出する(i=1,2,…,n/j=1,2,…,m)。算出された相互カーネルグラム行列Kxyは、後述する一般化固有値問題計算部23がこれを参照することができるよう、不図示の記憶装置に格納される。
【0042】
一般化固有値問題計算部23は、自己カーネルグラム行列計算部21により算出された自己カーネルグラム行列Kyと、相互カーネルグラム行列計算部22により算出された相互カーネルグラム行列Kxyとにより定義される一般化固有値問題KxyTKxyz=λKyzを解くことによって、r個の固有ベクトル{z1,z2,…,zr}を算出するための手段である。
【0043】
より具体的に言うと、一般化固有値問題計算部23は、(1)相互カーネルグラム行列Kxyの転置行列KxyTを算出し、(2)相互カーネルグラム行列Kxyとその転置行列KxyTとの行列積KxyTKxyを算出し、(3)一般化固有値問題KxyTKxyz=λKyzを解き、(4)得られた固有ベクトル(m次元の列ベクトル)のうち固有値の大きいものから順にr個の固有ベクトル{z1,z2,…,zr}を選択し、(5)選択したr個の固有ベクトル{z1,z2,…,zr}の各々を、ziTKyziのノルムが1になるように規格化する。規格化されたr個の固有ベクトル{z1,z2,…,zr}は、後述する特徴ベクトル計算部32がこれを参照することができるよう、不図示の記憶装置に格納される。
【0044】
なお、一般化固有値問題には公知の数値解法が幾つも存在しており、コンピュータ上で一般化固有値問題を解くためサブルーチンも広く利用されている。例えば、MATLAB(登録商標)に含まれているeigsやIntel Math Kernel Library(登録商標)に含まれているdsygvxなどは、その一例である。これらのサブルーチンを利用すれば、コンピュータを一般化固有値問題計算部23として機能させることができる。
【0045】
評価部30は、評価対象ベクトルxを特徴ベクトルy=ZTxΦに変換するための手段であり、例えば、図1に示したように、経験カーネル写像ベクトル計算部31と、特徴ベクトル計算部32とにより構成することができる。ここで、xΦは、カーネル関数値k(x,yj)を第j成分とするm次元ベクトルであり、「経験カーネル写像ベクトル」と称される。また、Zは、r個の固有ベクトル{z1,z2,…,zr}を並べたm×r行列[z1,z2,…,zr]である。
【0046】
評価部30を構成する各部が担う機能は、以下のとおりである。
【0047】
経験カーネル写像ベクトル計算部31は、入力された評価対象ベクトルxと、選択部10により選択されたm個の標本ベクトル{y1,y2,…,ym}とから、経験カーネル写像ベクトルxΦを算出するための手段である。より具体的に言うと、経験カーネル写像ベクトル計算部31は、入力された評価対象ベクトルxと選択された標本ベクトルyjとを記憶装置から読み出し、これらをカーネル関数k(x、y)に代入することによって、m次元の列ベクトルである経験カーネル写像ベクトルxΦの第j成分(xΦ)j=k(x,yj)を算出する(j=1,2,…,m)。算出された経験カーネル写像ベクトルxΦは、後述する特徴ベクトル計算部32がこれを参照することができるよう、不図示の記憶装置に格納される。
【0048】
特徴ベクトル計算部32は、一般化固有値問題計算部23により算出されたr個の固有ベクトル{z1,z2,…,zr}と、経験カーネル写像計算部21により算出された経験カーネル写像ベクトルxΦとから、特徴ベクトルy=ZTxΦを算出するための手段である。より具体的に言うと、特徴ベクトル計算部32は、規格化された固有ベクトルziと経験カーネル写像ベクトルxΦとを記憶装置から読み出し、これらの内積を算出することによって、r次元ベクトルである特徴ベクトルyの第i成分を算出する(i=1,2,…,r)。あるいは、行列ZTに経験カーネル写像ベクトルxΦを右から乗ずることによって、特徴ベクトルyを算出する。
【0049】
なお、算出する特徴ベクトルyの次元rは、入力される評価対象ベクトルxの次元dより高く設定されていてもよいし、低く設定されていてもよい。前者の場合、ノイズに強い冗長な特徴ベクトルyを得ることができ(冗長情報付加)、後者の場合、伝送効率に優れたデータサイズの小さい特徴ベクトルyを得ることができる(情報圧縮)。
【0050】
また、本実施形態においては、与えられたn個の標本ベクトル{x1,x2,…,xn}と、n個の標本ベクトル{x1,x2,…,xn}から選択されたm個の標本ベクトル{y1,y2,…,ym}とから算出された自己カーネルグラム行列Ky、相互カーネルグラム行列Kxy、及び、経験カーネル写像ベクトルxΦを用いて部分カーネル主成分分析を行う構成を示したが、本発明はこれに限定されるものではない。すなわち、後述する〔部分カーネル主成分分析の原理〕からも明らかなように、n個の標本ベクトル{x1,x2,…,xn}と、これとは別に与えられたm個の標本ベクトル{y1,y2,…,ym}とにより定義される自己カーネルグラム行列Ky、相互カーネルグラム行列Kxy、及び、経験カーネル写像ベクトルxΦを用いて部分カーネル主成分分析を行う構成を採用してもよい。この場合、自己カーネルグラム行列計算部21、相互カーネルグラム行列計算部22、及び、経験カーネル写像ベクトル計算部31が、n個の標本ベクトル{x1,x2,…,xn}と同様に、m個の標本ベクトル{y1,y2,…,ym}を直接外部から取得するようにすればよい。
【0051】
また、本実施形態においては、一般化固有値問題KxyTKxyz=λKyzを解くことによって、部分カーネル主成分分析を行う構成を示したが、本発明はこれに限定されるものではない。すなわち、一般化固有値問題KxyTKxyz=λKyzに代えて、正則化一般化固有値問題KxyTKxy(KxyTKxy+μKy)KxyTKxyz=λKyzを解くことによって、部分カーネル主成分分析を行う構成を採用してもよい。なお、正則化一般化固有値問題については、後述する〔部分カーネル主成分分析の原理〕を参照されたい。
【0052】
(カーネル主成分分析装置の構成例)
SKPCA装置1は、コンピュータ(電子計算機)を用いて構成することができる。図2は、SKPCA装置1として利用可能なコンピュータ100の構成を例示したブロック図である。
【0053】
コンピュータ100は、図2に示したように、バス110を介して互いに接続された演算装置120と、主記憶装置130と、補助記憶装置140と、入出力インタフェース150とを備えている。演算装置120として利用可能なデバイスとしては、CPU(Central Processing Unit)を挙げることができる。また、主記憶装置130として利用可能なデバイスとしては、例えば、半導体RAM(random access memory)を挙げることができる。また、補助記憶装置140として利用可能なデバイスとしては、例えば、ハードディスクドライブを挙げることができる。
【0054】
入出力インタフェース150には、図2に示したように、入力装置200及び出力装置300が接続される。ユーザにより指定された数値を入力データ(標本ベクトル及び評価対象ベクトル)とする場合には、例えば、キーボードを入力装置200として利用することができる。また、測定値を入力データとする場合には、例えば、その測定値に応じた測定器(センサ)を入力装置200として利用することもできる。また、出力データ(特徴ベクトル)を数値列又はグラフとしてユーザに提示する場合、例えば、モニタやプリンタなどを出力装置300として利用することができる。
【0055】
なお、出力装置300を介して出力データを出力する代わりに、記録媒体に出力データを記録するようにしてもよい。また、出力データを出力装置300に出力する代わりに、他の装置に出力データを送信するようにしてもよい。
【0056】
補助記憶装置140には、コンピュータ100をSKPCA装置1として動作させるためのカーネル主成分分析プログラム(以下「KPCAプログラム」と略記する)が格納されている。KPCAプログラムは、選択プログラムと、自己カーネルグラム行列計算プログラムと、相互カーネルグラム行列計算プログラムと、一般化固有値問題計算プログラムと、経験カーネル写像ベクトル計算プログラムと、特徴ベクトル計算プログラムとを含んでいる。
【0057】
演算装置120は、主記憶装置130上に展開された標本プログラムに含まれる命令を実行することによって、コンピュータ100を選択部10として機能させる。同様に、主記憶装置130上に展開された自己カーネルグラム行列計算プログラム、相互カーネルグラム行列計算プログラム、一般化固有値問題計算プログラム、経験カーネル写像ベクトル計算プログラム、及び、特徴ベクトル計算プログラムに含まれる命令を実行することによって、コンピュータ100を自己カーネルグラム行列計算部21、相互カーネルグラム行列計算部22、一般化固有値問題計算部23、経験カーネル写像ベクトル計算部31、及び、特徴ベクトル計算部32として機能させる。
【0058】
KPCAプログラムを実行する過程で生成される中間データ、すなわち、標本ベクトル{y1,y2,…,ym}、相互カーネルグラム行列Kxy、自己カーネルグラム行列Ky、相互カーネルグラム行列の転置行列KxyT、相互カーネルグラム行列Kxyとその転置行列KxyTとの行列積KxyTKxy、固有ベクトル{z1,z2,…,zr}、及び、経験カーネル写像ベクトルxΦは、演算装置120がこれを参照することができるよう主記憶装置130に格納される。ただし、主記憶装置130の記憶容量に制約がある場合には、これらの中間データを補助記憶装置140に格納するようにしてもよい。他のデータと比べてサイズの大きい相互カーネルグラム行列Kxyだけを補助記憶装置140に格納するような構成も有効である。
【0059】
(カーネル主成分分析方法)
次に、部分カーネル主成分分析方法(以下、「SKPCA方法」と略記する)について、図3〜図6を参照して説明する。
【0060】
図3は、本実施形態に係るSKPCA方法S1の流れを示したフローチャートである。SKPCA方法S1は、SKPCA装置1を用いたSKPCA方法であり、図3に示したように、選択ステップS10と、設計ステップS20と、評価ステップS30とを含んでいる。また、図3に示したように、標本ベクトル入力ステップSin1と、評価対象ベクトル入力ステップSin2と、特徴ベクトル出力ステップSoutとを更に含んでいる。
【0061】
標本ベクトル入力ステップSin1においては、SKPCA装置1が、n個の標本ベクトル{x1,x2,…,xn}の入力を受け付ける。換言すれば、n個の標本ベクトル{x1,x2,…,xn}を入力装置等の外部装置から取得する。
【0062】
選択ステップS10においては、SKPCA装置1の選択部10が、標本ベクトル入力ステップSin1にて入力されたn個の標本ベクトル{x1,x2,…,xn}からm個の標本ベクトル{y1,y2,…,ym}を選択する。
【0063】
設計ステップS20においては、SKPCA装置1の設計部20が、一般化固有値問題KxyTKxyz=λKyzを解くことによって、r個の固有ベクトル{z1,z2,…,zr}を算出する。自己カーネルグラム行列Ky、及び、相互カーネルグラム行列Kxyは、上述したとおり、標本ベクトル入力ステップSin1にて入力されたn個の標本ベクトル{x1,x2,…,xn}、及び、選択ステップS10にて選択されたm個の標本ベクトル{y1,y2,…,ym}に基づいて定義することができる行列である。
【0064】
評価対象ベクトル入力ステップSin2においては、SKPCA装置1が、評価対象ベクトルxの入力を受け付ける。換言すれば、評価対象ベクトルxを入力装置等の外部装置から取得する。なお、評価対象ベクトル入力ステップSin2は、評価ステップS30より前に実行されればよく、設計ステップS20より後に実行されることを要さない。すなわち、設計ステップS20より前に、あるいは、選択ステップS10より前に実行されてもよい。
【0065】
評価ステップS30においては、SKPCA装置1の評価部30が、設計ステップS20にて算出されたr個の固有ベクトル{z1,z2,…,zr}とを用いて、評価対象ベクトル入力ステップSin2にて入力された評価対象ベクトルxを特徴ベクトルy=ZTxΦに変換する。
【0066】
特徴ベクトル出力ステップSoutにおいては、SKPCA装置1が、評価ステップS30にて算出された特徴ベクトルyを出力する。例えば、モニタを用いて特徴ベクトルyを数値列又はグラフとして表示したり、プリンタを用いて特徴ベクトルyを数値又はグラフとして印刷したりする。なお、特徴ベクトルyを表示したり印刷したりする代わりに、特徴ベクトルyを記録媒体に記録したり他の装置に送信したりしてもよい。
【0067】
なお、特徴ベクトルyをグラフとして表示または印刷する場合、特徴ベクトルyの次元が1であれば直線上の点としてこれをプロットすることができるし、特徴ベクトルyの次元が2であれば平面上の点としてこれをプロットすることができるし、特徴ベクトルyの次元が3であれば、(仮想)3次元空間上の点としてこれをプロットすることができる。この場合、評価対象ベクトルxと合わせて表示すれば、評価対象ベクトルxと特徴ベクトルyとの関係も一目瞭然である。
【0068】
図4は、選択ステップS10の構成例を示したフローチャートである。選択ステップS10は、例えば図4に示したように、クラスタリングステップS11と、標本ベクトル選択ステップS12とにより構成することができる。
【0069】
クラスタリングステップS11においては、選択部10が、標本ベクトル入力ステップSin1にて入力されたn個の標本ベクトル{x1,x2,…,xn}をm個のクラスタ{C1,C2,…,Cm}にクラスタリングする。
【0070】
標本ベクトル選択ステップS12においては、選択部10が、クラスタリングステップS11にてクラスタリングされたm個のクラスタ{C1,C2,…,Cm}の各々からm個の標本ベクトル{y1,y2,…,ym}の各々を選択する。
【0071】
なお、クラスタリングステップS11においては、Φ(xi)が属する特徴空間Fにおける距離を用いたクラスタリングを行うことができる。これにより、標本ベクトルxiが属する空間Rdにおける距離を用いたクラスタリングを行う場合と比べて、より精度の高い特徴ベクトルを得ることができる。特徴空間Fにおける距離としては、例えば、‖Φ(xi)−Φ(xj)‖2=k(xi,xi)+k(xj,xj)−2k(xi,xj)が挙げられる。
【0072】
クラスタリングステップS11において利用可能な公知のクラスタリング手法としては、階層化クラスタリングやK-meansなどを挙げることができる。例えば、K-meansを利用した場合、(1)初期クラスタ重心{<C1>,<C2>,…,<Cm>}をn個の標本ベクトル{x1,x2,…,xn}から適当に選び出し、(2)各標本ベクトルxjを、特徴空間Fにおける距離‖Φ(xj)−<Ci>‖2が最小となるクラスタCiに割り振り、(3)各クラスタ重心<Ci>を、<Ci>=(1/|Ci|)Σx∈CiΦ(x)により更新する処理を、クラスタ重心{<C1>,<C2>,…,<Cm>}が更新されなくなるまで繰り返すことによって、n個の標本ベクトル{x1,x2,…,xn}をm個のクラスタ{C1,C2,…,Cm}にクラスタリングすることができる。
【0073】
また、標本ベクトル選択ステップS12においては、各クラスタCiに属する標本ベクトルのうち、特徴空間FにおいてクラスタCiの重心に最も近い標本ベクトル、すなわち、argminx∈Ci‖Φ(x)−<Ci>‖2を取り出し、これを標本ベクトルyiとすることが好ましい。あるいは、クラスタCiに属する標本ベクトルのうち、入力空間Rdにおいてクラスタ重心Ciに最も近い標本ベクトル(いわゆるPre-image)を取り出し、これを標本ベクトルyiとすることが好ましい。これにより、各クラスタから他の標本ベクトルを取り出す場合と比べて、より精度の高い特徴ベクトルを得ることができる。なお、Pre-imageについては、以下の文献を参照されたい。
【0074】
S. Mika, B. Scholkopf and A. Smola,“Kernel PCA and denoising in feature space”,Advances in neural information processing systems (NIPS),11,pp,536-542 (1999)。
【0075】
B. Scholkopf,S. Mika,C. Burges,P. Knirsch,K.-R. Muller,G. Ratsch and A. Smola,“Input space vs. feature space in kernel-based methods”,IEEE Transactions on Neural Networks,10,5,pp. 1000-1017 (1999)。
【0076】
M. Girolami,“Mercer kernel-based clustering in feature space”,IEEE trans. on neural networks,13,3,pp. 780-784(2002)。
【0077】
なお、選択ステップS10の構成は、図4に示したものに限らない。特に、SKPCA方法S1では近似誤差あるいは残差を容易に算出することができるので、前向き選択や後向き選択などの標本選択の手法を容易に導入することができる。更に、無作為抽出されたm個の標本ベクトル{y1,y2,…,ym}を用いたSKPCA方法S1を繰り返し、所望の精度を有する特徴ベクトルyを算出するような構成を採ることもできる。
【0078】
図5は、設計ステップS20の構成例を示したフローチャートである。設計ステップ20は、例えば図5に示したように、自己カーネルグラム行列計算ステップS21と、相互カーネルグラム行列計算ステップS22と、一般化固有値問題計算ステップS23とにより構成することができる。
【0079】
自己カーネルグラム行列計算ステップS21においては、評価部20の自己カーネルグラム行列計算部21が、選択ステップ10にて選択されたm個の標本ベクトル{y1,y2,…,ym}から、自己カーネルグラム行列Kyを算出する。
【0080】
相互カーネルグラム行列計算ステップS22においては、評価部20の相互カーネルグラム行列計算部22が、標本ベクトル入力ステップSin1にて入力されたn個の標本ベクトル{x1,x2,…,xn}と、選択ステップ10にて選択されたm個の標本ベクトル{y1,y2,…,ym}とから、相互カーネルグラム行列Kxyを算出する。
【0081】
一般化固有値問題計算ステップS23においては、評価部20の一般化固有値問題計算部23が、自己カーネルグラム行列計算ステップS21にて算出された自己カーネルグラム行列Kyと、相互カーネルグラム行列計算ステップS22にて算出された相互カーネルグラム行列Kxyとにより定義される一般化固有値問題KxyTKxyz=λKyzを解くことによって、r個の固有ベクトル{z1,z2,…,zr}を算出する。
【0082】
なお、自己カーネルグラム行列計算ステップS21及び相互カーネルグラム行列計算ステップS22は、一般化固有値問題計算ステップS23より以前に実行されればよく、これらの実行順序は図5に示したものに限定されない。すなわち、図5においては自己カーネルグラム行列計算ステップS21を実行した後で相互カーネルグラム行列計算ステップS22を実行するようにしているが、相互カーネルグラム行列計算ステップS22を実行した後で自己カーネルグラム行列計算ステップS21を実行するようにしてもよい。
【0083】
図6は、評価ステップS30の構成例を示したフローチャートである。評価ステップS30は、例えば図6に示したように、経験カーネル写像ベクトル計算ステップS31と、特徴ベクトル計算ステップS32と、により構成することができる。
【0084】
経験カーネル写像ベクトル計算ステップS31においては、評価部30の経験カーネル写像ベクトル計算部31が、評価対象ベクトル取得ステップSin2にて入力された評価対象ベクトルxと、選択ステップ10にて選択されたm個の標本ベクトル{y1,y2,…,ym}とから、経験カーネル写像ベクトルxΦを算出する。
【0085】
特徴ベクトル計算ステップS32においては、評価部30の特徴ベクトル計算部32が、一般化固有値問題計算ステップS23にて算出されたr個の固有ベクトル{z1,z2,…,zr}と、経験カーネル写像計算ステップS21にて算出された経験カーネル写像ベクトルxΦとから、特徴ベクトルyを算出する。
【0086】
〔部分カーネル主成分分析の応用〕
部分カーネル主成分分析は、カーネル主成分分析と同様、雑音除去、パターン分類、パターン検出、欠損値補完、統計的推定、統計的予測、脳コンピュータインタフェース(BCI)などに応用することができる。これらの問題に部分カーネル主成分分析を適用する仕方は、これらの問題に従来のカーネル主成分分析を適用する仕方と同様である。
【0087】
例えば、部分カーネル主成分分析を用いた雑音除去方法は、従来、カーネル主成分分析により得られた特徴ベクトルを用いて行われていた逆変換写像の計算を、部分カーネル主成分分析により得られた特徴ベクトルを用いて行うようにすることにより実現することができる。逆変換写像の計算に部分カーネル主成分分析を用いた場合、従来のカーネル主成分分析を用いた場合と比べて、少ない計算量で効率の良い雑音除去を行うことができる。
【0088】
パターン分類、パターン検出、及び、欠損値補間においては、例えば、以下のようにして部分主成分分析方法を用いることができる。
【0089】
パターン分類は、p個のクラス{A1,A2,…,Ap}に分類されているq個の標本ベクトル{s1,s2,…,sq}基づき、対象ベクトルtを分類すべきクラスを決定する方法である。(1)各クラスAiに分類されているni個の標本ベクトル{si1,si2,…,sini}に基づく部分カーネル主成分分析を実行することによって、対象ベクトルtの特徴ベクトルuiを各j=1,…,pについて算出し、(2)特徴ベクトルujのノルムが最大となるクラスAjに対象ベクトルtを分類すれば、少ない計算量で精度良くパターン分類を行うことができる。
【0090】
パターン検出は、或るパターンを有するq個の標本ベクトル{s1,s2,…,sq}に基づき、対象ベクトルtがそのパターンを有するか否かを判定する方法である。(1)
q個の標本ベクトル{s1,s2,…,sq}に基づく部分カーネル主成分分析を実行することによって、対象ベクトルtの特徴ベクトルuを算出し、(2)特徴ベクトルuのノルムを予め定められた閾値Thと比較することによって、対象ベクトルtが特定のパターンを有するか否かを判定すれば、少ない計算量で精度良くパターン検出を行うことができる。
【0091】
欠損値補完は、q個の標本ベクトル{s1,s2,…,sq}に基づき、第k成分に欠損のある対象ベクトルtに対する欠損値補完を行う方法である。(1)第k成分を異なる値に設定したp個の対象ベクトル{t1,t2,…,tp}の各々について、q個の標本ベクトル{x1,x2,…,xq}に基づく部分カーネル主成分分析を実行することによって、対象ベクトルtiの特徴ベクトルuiを算出し、(2)特徴ベクトルujのノルムが最大となる対象ベクトルtjの第k成分の値を欠損のある対象ベクトルtの第k成分の値とすれば、少ない計算量で精度良く欠損値補間を行うことができる。
【0092】
なお、与えられたベクトルデータを対象ベクトルtと看做し、与えられたベクトルデータにおける未知の値を対象ベクトルtにおける欠損成分と看做せば、対象ベクトルtの欠損値補完を行うことにより、ベクトルデータにおける未知の値を統計的に推定することができる(統計的推定)。また、時系列データを対象ベクトルtと看做し、時系列データにおける未来の値を対象ベクトルtにおける欠損成分と看做せば、対象ベクトルtの欠損値補完を行うことにより、時系列データにおける未来の値を統計的に予測することができる(統計的予測)。
【0093】
更に、部分カーネル主成分分析は、脳コンピュータインタフェース(BCI)に応用することができる。脳信号の測定には、脳電図(EEG)、脳磁図(MEG)、近赤外光トポグラフィー(NIRS)、fMRIなどが用いられるが、ここでは、EEGを用いたBCIについて説明する。
【0094】
EEGによって得られた脳信号は、通常、多チャンネルであり、かつ、雑音を多く含む。そこで、BCIの前処理として、アーチファクト除去、バンドパスフィルタ(BPF)、CSP(Common Spatial Patterns)などの処理が施される。その後、入力信号は適当な時間幅をもつ窓で区切られ、データは数値列で表される。この数値列を評価対象ベクトルxとして部分カーネル主成分分析を利用する。この際、標本ベクトル{x1,x2,…,xn}は予め与えておく。そして、部分カーネル主成分分析により得られた特徴ベクトルyを、識別器で判別することによって、BCIの結果を得る。
【0095】
〔部分カーネル主成分分析の原理〕
次に、本発明の基礎となる部分カーネル主成分分析の原理について説明する。
【0096】
1.カーネル主成分分析
本節では、簡略にKPCAについて示した後、Mercerカーネル(1)を用いたKPCAの特徴付けを行う。
【0097】
【数1】

【0098】
x1,x2,…,xnをd次元の標本とする。特徴空間Fへ変換された標本Φ(x1),…,Φ(xn)の相関作用素RFは、(2)で与えられる。
【0099】
【数2】

【0100】
ここで,ケット-ブラ表記|・><・|は|a><b|c=<c,b>aを満たす作用素である。有限次元では転置・Tを用いた表記abTと同値であるが、Gaussianカーネルなどを用いた場合は、Fが無限次元となるためケット-ブラ表記を用いる。RFの固有値分解を(3)とおく。
【0101】
【数3】

【0102】
ここで固有値λiは降順に並んでいるとする。r次元の固有空間への変換UKと射影作用素PKは、(4)(5)で与えられる。
【0103】
【数4】

【0104】
【数5】

【0105】
ここでeriは、Rrのi番目の標準基底(i番目の要素が1でそれ以外の要素が0のベクトル)を表す。
【0106】
通常,RFは非常に大きいか、無限次元から無限次元への作用素であるため固有値分解が難しい。そこで、以下の作用素Sを考える。
【0107】
【数6】

【0108】
Sの随伴作用素をS*と書くと、RF=(1/n)SS*の固有値、固有ベクトルは、Kx=S*S=nΣni=1λiviviT、ui=(1/√λi)Sviの関係を満たす。これより、(7)(8)が得られる。
【0109】
【数7】

【0110】
【数8】

【0111】
ここで、(Kx)ij=k(xi,xj)はカーネルグラム行列と呼ばれる。入力xに対して、以下の出力を得る。
【0112】
【数9】

【0113】
【数10】

【0114】
ここで、‖・‖はEuclidノルムまたはl2ノルムを表し、S*Φ(x)=[k(x,x1),…,k(x,xn)]Tは経験カーネル写像と呼ばれるn次元ベクトルである。
【0115】
以上の議論より、UKあるいはPKを求めるためには、n×nの大きさの対称行列の固有値分解が必要であり,経験カーネル写像S*Φ(x)を求めるためにはn回のカーネル関数の計算が必要となる。さらに入力xの評価のために、すべての標本を保存しておく必要がある。このため、nが大きくなると計算量、メモリ量が問題となることがある。特に標本数が数万から数十万を超えるような大規模な問題ではKPCAを適用することができない。
【0116】
KPCAを拡張するために,KPCAの特徴付けを行う。主成分分析は、ランク制約の下で近似誤差を最小とする行列と定義できる。
【0117】
【数11】

【0118】
ここで、Exは平均を表す。KPCAについても同様の特徴付けができる。
【0119】
【数12】

【0120】
ここで、N(A)はAの核空間、R(A)はAの値域あるいは像を表す。制約N(X)⊃R(S)⊥は特徴空間F中のSが張る空間以外についても考慮する必要があるため必要となる。入力次元空間の問題では、標本数が充分にあれば全空間を張ることが多いため、核空間や値域の議論を省略することが多い。しかしながら、高次元の特徴空間では、標本が全空間を張らないことが多いため、これらを正確に扱うことが重要である。本明細書においてもこれらを正確に扱う。
【0121】
2. 部分カーネル主成分分析
前節で示した通り、KPCAは特徴空間Fで、標本Φ(x1),…,Φ(xn)が張るRnと同型の空間上で問題が議論される。すなわち。標本Φ(x1),…,Φ(xn)は基底を成す。KPCAはすべての標本を基底に用いるため、固有値分解の大きさやカーネル関数の評価回数が大きい。そこで、基底を少数の標本に置き換えることにより、この問題を解決する。
【0122】
y1,…,ym(m<n)を基底のための標本とし、作用素(11)を考える。
【0123】
【数13】

【0124】
この基底の下で全標本を最良に低階数近似する作用素を部分カーネル主成分分析(SKPCA:SubsetKPCA)と定義する。
【0125】
[定義1](SubsetKPCA)以下の最適化問題の解を部分KPCAと呼ぶ。
【0126】
【数14】

【0127】
Ky=T*T、Kxy=S*Tとおき、A+で作用素または行列のMoore−Penrose一般逆、A1/2で自己共役作用素あるいは対称行列の平方根A1/2AT/2=Aを表す。A1/2は一般に対称ではなく、一意ではない。行列平方根やCholesky分解などを用いることができる。次にSKPCAの解を示す。
【0128】
[定理1](SKPCAの解)(Ky1/2)+KxyTKxy(KyT/2)+の固有値分解を(13)とおく。
【0129】
【数15】

【0130】
ここで、ξi (i=1,…,m)は降順に並んでいるものとする。W=[w1,…,wr]とおくと、最適化問題(12)の解の1つは、以下で与えられる。
【0131】
【数16】

【0132】
特にR(T)⊂R(S)であるような場合、すなわち{yi}mi=1が{xi}ni=1の部分集合で与えられるような場合、(14)で与えられる。
【0133】
【数17】

【0134】
証明は後述する。
【0135】
[系1]R(T)⊂R(S)ならばPSは正射影である。
【0136】
(証明)明らかにPS*=PSである。(Ky1/2)+Ky(KyT/2)+は、R(Ky)への正射影であり、R(Ky)⊃R(W)であることに注意すると、PSPS=T(KyT/2)+WWT(Ky1/2)+Ky(KyT/2)+WWT(Ky1/2)+T*=PSであり、PSは正射影である(証明終)。
【0137】
[系2]基底にx1,…,xnを用いるとSKPCAはKPCAに一致する。
【0138】
明らかであるため,証明は省略する。
【0139】
次にSKPCAに別の表現を与える。
【0140】
[補題1]A,BをR(A)⊂ R(B)を満たす非負定値の行列とする。このとき、(B1/2)+A(BT/2)+の固有値λ、と固有ベクトルvは、任意のスカラーαに関して、Au=λBu、u=α(BT/2)+vを満たす。さらに、(λ,u)がAu=λBuを満たすとき、任意のスカラーβに対して、(B1/2)+A(BT/2)+v=λv、v=βBT/2u を満たす。
【0141】
[命題1]補題より、R(T)⊂ R(S)ならば、一般固有値問題KxyTKxyz=λKyzの固有値の上位r個に対応する固有ベクトル{zi}ri=1を用いて、(15)と表される。
【0142】
【数18】

【0143】
ここで、Z=[z1…zr]であり、z1,…,zrは,<zi|Kyzi>=1,(i=1,…,r)となるように正規化されているとする。
【0144】
R(T)⊂R(S)ならば、SKPCAによるr次元への変換は、US=ZTT*で与えられ、入力をxとすると(16)である。
【0145】
【数19】

【0146】
以上の議論より、SKPCAは大きさmの(一般)固有値問題に帰着する。評価時についてもm回のカーネル関数の計算で評価でき,m個の標本を保存しておくだけでよい。これ以降、R(T)⊂R(S)である、すなわちy1,…,ymはx1,…,xnの部分集合で与えられているとする。
【0147】
IKPCAでは、変換作用素は、異なる考え方から導き出され、(17)で与えられている。
【0148】
【数20】

【0149】
非特許文献2ではIKPCAは識別のための特徴抽出に(18)の形で用いられている。
【0150】
【数21】

【0151】
すなわち、SKPCAと比較すると各次元の要素が(1/√ξi)倍されている。この影響は後段の識別性能にはあまり影響しないと考えられるが、機械学習のための特徴抽出以外の応用においては大きな誤差が生じる。
【0152】
3.正則化
標本数が少ないとき、統計的推定量はしばしば標本に過適合(overfit)することがある。特に高次元中で問題を解くカーネルトリックは自由度が高いため過適合しやすい。線形逆問題や回帰問題(リッジ回帰)などにおいては、過適合を防ぐために(Tikhonov)正則化がよく用いられる。そこで、本手法にも過適合を防ぐために正則化を導入する。
【0153】
正則化は、パラメータベクトルあるいは行列のノルムを最小化することにより実現される。SKPCAの正則化を正則化SKPCA(RSKPCA:RegularizedSKPCA)と呼び、以下に定義を示す。
【0154】
[定義2](正則化SKPCA)
【0155】
【数22】

【0156】
ここで、μ>0は正則化パラメータ、‖・‖FはFrobeniusノルムを表す。目的関数の第2項は適合の度合いを表し、正則化パラメータμが適合度合いと近似誤差のトレードオフの調整を行う。
【0157】
正則化SKPCAの解を示す。
【0158】
[定理2](正則化SKPCAの解)KxyTKxy+μKyが正則であるとき、正則化SKPCAの解の1つは、(20)で与えられる。
【0159】
【数23】

【0160】
ここで、qiは固有値分解(21)の固有ベクトルとして与えられる。
【0161】
【数24】

【0162】
ここで、固有値σiは降順に並んでいるものとする。KxyTKxy+μKyが特異の場合には、逆行列は一般逆行列に置き換わる。
【0163】
SKPCAと同様に、(KyT/2)+qiは、一般固有値問題KxyTKxy(KxyTKxy+μKy)-1KxyTKxyp=λKypで計算することができる。
【0164】
[命題2]R(T)⊂R(S)であるとき、KxyTKxy+μKyが正則となる必要十分条件は、N(T)={0}である。
【0165】
(証明)(i)必要条件を示す。KxyTKxyとKyは非負定値であるため、どちらかが正定値であれば,KxyTKxy+μKyは正則である。N(T)={0}であれば明らかにKyは正則である。(ii)十分条件を示す。正則であれば明らかに正定値であり、任意のx∈Rm,x≠0に対して<x|(KxyTKxy+μKy)x>=‖S*Tx‖2+μ‖Tx‖2が正であるため、N(T)={0}である(証明終)。
【0166】
[命題3]GaussianカーネルK(x,y)=exp(−c‖x−y‖2)を用いた場合、y1,…,ymが互いに異なる場合、Kyは正定値である。
【0167】
以上の命題より、KxyTKxy+μKyはGaussianカーネルを用いた場合は、標本が重複しなければ正則であり、また、多項式カーネルk(x,y)=<x,y+c>dの場合においても、dが充分に大きければKyは正則となる。
【0168】
正則化パラメータμは交差検定(cross validation)などにより実験的に決定出来る。教師なし学習として用いる場合は、学習用標本とは別に検定用標本z1,…,zlを用意し、その検定用標本の近似誤差Σli=1‖Φ(zi)−PRΦ(zi)‖2を最小化するようなμを探す。検定用標本と学習用標本を入れ替え、交差検定を行うことで最適な正則化パラメータが推定できる。
【0169】
〔数値実験による検証〕
次に、本発明の効果を検証するための数値実験について説明する。
【0170】
1.人工データによる実験
本実験においては、図7の(a)に示す2次元の1000個のデータを利用した。図7の(b)は、Gaussianカーネルk(x,y)=exp(−0.1‖x−y‖2)を用いたKPCAで5次元の部分空間への射影ノルムの等高線を表す。図7の(c)に、標本を無作為に50個選び出し、KPCAを行った結果を表す。簡便のため、これ以降、(b)のように標本すべてを用いたKPCAを全体KPCAと呼び、(c)のように標本の一部を使って求めたKPCAを縮減KPCAと呼ぶ。図7の(d)は縮減KPCAと同じ標本を基底に用いたSKPCA、図7の(e)は縮減KPCAと同じ標本を基底に用いたRSKPCA(μ=0.1)、図7の(f)はIKPCAを示す。
【0171】
定量的評価には2つの手法を用いた。1つ目の評価基準は、全標本に対する近似誤差(残差)である。
【0172】
【数25】

【0173】
Xは、PKやPSで置き換えられる。もう1つの評価基準は全体KPCAからの距離である。m次元中のr次元空間部分空間への正射影行列の全体の集合はGrassmann多様体(Grassmannian)と呼ばれ、その空間における距離の1つは射影行列の差のノルムで与えられる。KPCAとSKPCAも特徴空間F中のr次元部分空間への正射影作用素であるため、差のノルムで距離を定義する。ノルムにはFrobeniusノルムを用いた。全体KPCAの正射影作用素をPFKとおき、距離の2乗を全体KPCAのノルムの2乗‖PFK‖F2で割ったものを正規化距離Dとして定義する。
【0174】
【数26】

【0175】
図より、提案手法は全体KPCAとほとんど変わらない等高線を描くことが分かる。一方、縮減KPCAとIKPCAの等高線はKPCAから大きくかけ離れたものとなっている。近似誤差Eと正規化距離Dにおいても、提案手法は全体KPCAとほぼ変わらないのに対して、縮減KPCA、IKPCAはどちらも大きな値となっている。
【0176】
Intel Core2 Duo(登録商標) 2.16GHzを搭載したMacBook(登録商標)でMATLAB(登録商標)のIRAMを利用した固有値分解の関数eigsでは、1000×1000の対称行列の固有値分解で0.4秒、50×50の対称行列の固有値分解で0.02秒であった。この実験の場合では、提案法と縮減KPCAは、全体KPCAの場合より20倍高速に固有値分解を行うことができる。さらにカーネル関数の評価回数も20 分の1の回数で計算ができる。
【0177】
2.実データを用いた実験
UCI Machine learning repositoryにあるconcreteとhousingのデータセットを用いて実験を行った。concreteは9次元、1030個の標本があり、housingは14次元、506個の標本がある。カーネル関数にはGaussianカーネルを用い、パラメータcには、全要素の分散σ から、c=1/2σ2を求めて用いた。階数は入力次元と同じ次元で実験を行った。
【0178】
図8の(a)及び(b)は全体KPCAからの正規化距離を示す。IKPCAは、比較できない程度の大きな距離を示したため省略した。標本の部分集合は無作為抽出で行い、100回の無作為抽出の平均、標準偏差、最小値を示す。図より、標本数が全体の20%から10%程度であっても提案手法は全体KPCAから1%程度の誤差しか生じないことが確認できる。図9の(a)及び(b)は式(22)の誤差を全体KPCAの誤差で割った正規化誤差を示す。標本数が20%程度に減少した場合でも、正規化誤差の最小値は、全体KPCAの誤差の1.01倍程度であることが分かる。図10の(a)及び(b)は設計時の計算時間を示す。数値計算はIntel Math Kernel Library(登録商標)を用い、全体KPCA、縮減KPCAの固有値分解にはdsyevx、SKPCAの一般固有値分解には、dsygvxを用いた。図より、基底に用いる標本数が全標本数の70%以下の場合、提案手法の方が高速に設計を行うことができることがわかる。
【0179】
図11はhousingにおける無作為抽出と特徴空間中K‐meansによる標本選択の比較である。K‐meansの方が平均的によい近似性能を示し、標準偏差も小さいことが確認できる。
【0180】
最後に、正則化の効果を示すためにhousingの部分集合として100個(n=100)、基底にm個の標本を用いて、この部分集合に対する近似を最小にするSKPCA及び、正則化SKPCAを求め、それぞれの全体KPCAからの正規化距離を比較した。100回の試行における正規化距離の平均値を表1に示す。実験結果より、正則化を用いた方がよい近似を与えることが確認できた。
【0181】
【表1】

【0182】
〔定理の証明〕
[補題2]制約条件N(X)⊃R(T)⊥は、ある作用素A:Rm→Fを用いて、X=AT*と表されることと同値である。
【0183】
【数27】

【0184】
(証明)(i)<=はR(T)⊥=N(T)⊂N(X)より明らかである。(ii)⇒の方向、すなわち、「N(X)⊃R(T)⊥のときX=AT*となるAが存在する。」を示す。A=X(T*)+とおけばAT*=X(T*)+T*=XPR(T)=X(I−PR(T)⊥)である。ここで、Pχはχへの正射影を表す。N(X)⊃R(T)⊥より、XPR(T)⊥=0であり、AT*=Xとなる。(i),(ii)より補題を得る(証明終)。
【0185】
[補題3]制約条件R(X)⊂R(T)⊥は、ある作用素A:F→Rmを用いて、X=TAと表されることと同値である。
【0186】
証明は、補題2と同様なので省略する。
【0187】
定理2でμ=0とおけば定理1となるため、μ≧0として定理2のみを証明する。補題2,3よりX=TAT*とおける。作用素Aに対するトレースを任意の正規直交基底ui,i=1,…を用いてTrace(A)=Σi<ui|Aui>と定義する。最適化問題(19)の目的関数をJとおくと以下のとおりである。
【0188】
【数28】

【0189】
R(KxyT)=R(T*S)⊂R(T*)=R(Ky)より、KxyT=PR(Ky)KxyT=KyKy+KxyTであり、Kxy=Kxy(KyT/2)+KyT/2である。また、R(KxyTKxy+μKy)⊃R(KxyT)より、PR(KxyTKxy+μKy)KxyT=(KxyTKxy+μKy)1/2((KxyTKxy+μKy)1/2)+KxyT=KxyTである。これより、以下のようになる。
【0190】
【数29】

【0191】
ここでCはAに対する定数項を表す。式(21) の固有値分解より、特異値分解を以下のように置く。
【0192】
【数30】

【0193】
Schmidtの近似定理(Eckart−Youngの定理)より、以下を満たすAが存在するときは、上式を満たすAがJを最小化する。
【0194】
【数31】

【0195】
【数32】

【0196】
以上より、式(A.1)を満たすAが存在し、その解の一つは、以下で与えられる。
【0197】
【数33】

【0198】
証明終
【産業上の利用可能性】
【0199】
本発明は、カーネル主成分分析を用いたデータ解析一般に広く適用することができる。特徴抽出、雑音除去、パターン分類、パターン検出、欠損値補完、統計的推定、統計的予測などに好適に利用することができる。
【符号の説明】
【0200】
1 SKPCA装置(カーネル主成分分析装置)
10 選択部(選択手段)
20 設計部(設計手段)
21 自己カーネルグラム行列計算部
22 相互カーネルグラム行列計算部
23 一般化固有値問題計算部
30 評価部(評価手段)
31 経験カーネル写像ベクトル計算部
32 特徴ベクトル計算部
【特許請求の範囲】
【請求項1】
カーネル主成分分析装置を用いて、標本として与えられたn個のd次元ベクトル{x1,x2,…,xn}に基づき、評価対象として与えられたd次元ベクトルxの特徴を表現するr次元ベクトルyを算出するカーネル主成分分析方法であって、
上記n個のd次元ベクトル{x1,x2,…,xn}からm個(mはn未満の自然数)のd次元ベクトル{y1,y2,…,ym}を選択する選択ステップ、又は、上記n個のd次元ベクトル{x1,x2,…,xn}とは別にm個のd次元ベクトル{y1,y2,…,ym}を取得する取得ステップと、
カーネル関数値k(yi,yj)を第ij成分とするm×m行列をKyとし、カーネル関数値k(xi,yj)を第ij成分とするn×m行列をKxyとして、一般化固有値問題KxyTKxyz=λKyz、又は、正則化一般化固有値問題KxyTKxy(KxyTKxy+μKy)KxyTKxyz=λKyzを解くことによって、r個の固有ベクトル{z1,z2,…,zr}を算出する設計ステップと、
上記r個の固有ベクトル{z1,z2,…,zr}を用いて、上記d次元ベクトルxを上記r次元ベクトルyに変換する評価ステップと、を含んでいる、
ことを特徴とするカーネル主成分分析方法。
【請求項2】
上記設計ステップは、
上記m個のd次元ベクトル{y1,y2,…,ym}から、上記m×m行列Kyを算出するステップと、
上記n個のd次元ベクトル{x1,x2,…,xn}、及び、上記m個のd次元ベクトル{y1,y2,…,ym}から、上記n×m行列Kxyを算出するステップと、
上記一般化固有値問題KxyTKxyz=λKyz、又は、上記正則化一般化固有値問題KxyTKxy(KxyTKxy+μKy)KxyTKxyz=λKyzを解くことによって、上記r個の固有ベクトル{z1,z2,…,zr}を算出するステップと、を含んでおり、
上記評価ステップは、
上記d次元ベクトルx、及び、上記m個のd次元ベクトル{y1,y2,…,ym}から、カーネル関数値k(x,yj)を第j成分とするm次元ベクトルxΦを算出するステップと、
上記r個の固有ベクトル{z1,z2,…,zr}、及び、上記m次元ベクトルxΦから、上記r次元ベクトルy=[z1,z2,…,zr]TxΦを算出するステップと、を含んでおり、
当該カーネル主成分分析方法は、上記評価ステップにて算出された上記r次元ベクトルyを他の装置に出力する出力ステップを更に含んでいる、
ことを特徴とする請求項1に記載のカーネル主成分分析方法。
【請求項3】
上記選択ステップは、
上記n個のd次元ベクトル{x1,x2,…,xn}をm個のクラスタ{C1,C2,…,Cm}にクラスタリングするステップと、
上記m個のクラスタ{C1,C2,…,Cm}の各々から上記m個のd次元ベクトル{y1,y2,…,ym}の各々を選択するステップと、を含んでいる、
ことを特徴とする請求項1または2に記載のカーネル主成分分析方法。
【請求項4】
上記選択ステップにおいて、上記n個のd次元ベクトル{x1,x2,…,xn}をm個のクラスタ{C1,C2,…,Cm}にクラスタリングする際に、特徴空間上のノルムを使用する、
ことを特徴とする請求項3に記載のカーネル主成分分析方法。
【請求項5】
上記ベクトルyの次元rは、上記ベクトルxの次元dよりも小さい、
ことを特徴とする請求項1から4までの何れか1項に記載のカーネル主成分分析方法。
【請求項6】
上記ベクトルyの次元rは、上記ベクトルxの次元dよりも大きい、
ことを特徴とする請求項1から4までの何れか1項に記載のカーネル主成分分析方法。
【請求項7】
標本として与えられたn個のd次元ベクトル{x1,x2,…,xn}に基づき、評価対象として与えられたd次元ベクトルxの特徴を表現するr次元ベクトルyを算出するカーネル主成分分析装置であって、
上記n個のd次元ベクトル{x1,x2,…,xn}からm個(mはn未満の自然数)のd次元ベクトル{y1,y2,…,ym}を選択する選択手段、又は、上記n個のd次元ベクトル{x1,x2,…,xn}とは別にm個のd次元ベクトル{y1,y2,…,ym}を取得する取得手段と、
カーネル関数値k(yi,yj)を第ij成分とするm×m行列をKyとし、カーネル関数値k(xi,yj)を第ij成分とするn×m行列をKxyとして、一般化固有値問題KxyTKxyz=λKyz、又は、正則化一般化固有値問題KxyTKxy(KxyTKxy+μKy)KxyTKxyz=λKyzを解くことによって、r個の固有ベクトル{z1,z2,…,zr}を算出する設計手段と、
上記r個の固有ベクトル{z1,z2,…,zr}を用いて、上記d次元ベクトルxを上記r次元ベクトルyに変換する評価手段と、とを備えている、
ことを特徴とするカーネル主成分分析装置。
【請求項8】
コンピュータを請求項7に記載のカーネル主成分分析装置として動作させるためのためのカーネル主成分分析プログラムであって、上記コンピュータを上記カーネル主成分分析装置が備えている各手段として機能させるカーネル主成分分析プログラム。
【請求項1】
カーネル主成分分析装置を用いて、標本として与えられたn個のd次元ベクトル{x1,x2,…,xn}に基づき、評価対象として与えられたd次元ベクトルxの特徴を表現するr次元ベクトルyを算出するカーネル主成分分析方法であって、
上記n個のd次元ベクトル{x1,x2,…,xn}からm個(mはn未満の自然数)のd次元ベクトル{y1,y2,…,ym}を選択する選択ステップ、又は、上記n個のd次元ベクトル{x1,x2,…,xn}とは別にm個のd次元ベクトル{y1,y2,…,ym}を取得する取得ステップと、
カーネル関数値k(yi,yj)を第ij成分とするm×m行列をKyとし、カーネル関数値k(xi,yj)を第ij成分とするn×m行列をKxyとして、一般化固有値問題KxyTKxyz=λKyz、又は、正則化一般化固有値問題KxyTKxy(KxyTKxy+μKy)KxyTKxyz=λKyzを解くことによって、r個の固有ベクトル{z1,z2,…,zr}を算出する設計ステップと、
上記r個の固有ベクトル{z1,z2,…,zr}を用いて、上記d次元ベクトルxを上記r次元ベクトルyに変換する評価ステップと、を含んでいる、
ことを特徴とするカーネル主成分分析方法。
【請求項2】
上記設計ステップは、
上記m個のd次元ベクトル{y1,y2,…,ym}から、上記m×m行列Kyを算出するステップと、
上記n個のd次元ベクトル{x1,x2,…,xn}、及び、上記m個のd次元ベクトル{y1,y2,…,ym}から、上記n×m行列Kxyを算出するステップと、
上記一般化固有値問題KxyTKxyz=λKyz、又は、上記正則化一般化固有値問題KxyTKxy(KxyTKxy+μKy)KxyTKxyz=λKyzを解くことによって、上記r個の固有ベクトル{z1,z2,…,zr}を算出するステップと、を含んでおり、
上記評価ステップは、
上記d次元ベクトルx、及び、上記m個のd次元ベクトル{y1,y2,…,ym}から、カーネル関数値k(x,yj)を第j成分とするm次元ベクトルxΦを算出するステップと、
上記r個の固有ベクトル{z1,z2,…,zr}、及び、上記m次元ベクトルxΦから、上記r次元ベクトルy=[z1,z2,…,zr]TxΦを算出するステップと、を含んでおり、
当該カーネル主成分分析方法は、上記評価ステップにて算出された上記r次元ベクトルyを他の装置に出力する出力ステップを更に含んでいる、
ことを特徴とする請求項1に記載のカーネル主成分分析方法。
【請求項3】
上記選択ステップは、
上記n個のd次元ベクトル{x1,x2,…,xn}をm個のクラスタ{C1,C2,…,Cm}にクラスタリングするステップと、
上記m個のクラスタ{C1,C2,…,Cm}の各々から上記m個のd次元ベクトル{y1,y2,…,ym}の各々を選択するステップと、を含んでいる、
ことを特徴とする請求項1または2に記載のカーネル主成分分析方法。
【請求項4】
上記選択ステップにおいて、上記n個のd次元ベクトル{x1,x2,…,xn}をm個のクラスタ{C1,C2,…,Cm}にクラスタリングする際に、特徴空間上のノルムを使用する、
ことを特徴とする請求項3に記載のカーネル主成分分析方法。
【請求項5】
上記ベクトルyの次元rは、上記ベクトルxの次元dよりも小さい、
ことを特徴とする請求項1から4までの何れか1項に記載のカーネル主成分分析方法。
【請求項6】
上記ベクトルyの次元rは、上記ベクトルxの次元dよりも大きい、
ことを特徴とする請求項1から4までの何れか1項に記載のカーネル主成分分析方法。
【請求項7】
標本として与えられたn個のd次元ベクトル{x1,x2,…,xn}に基づき、評価対象として与えられたd次元ベクトルxの特徴を表現するr次元ベクトルyを算出するカーネル主成分分析装置であって、
上記n個のd次元ベクトル{x1,x2,…,xn}からm個(mはn未満の自然数)のd次元ベクトル{y1,y2,…,ym}を選択する選択手段、又は、上記n個のd次元ベクトル{x1,x2,…,xn}とは別にm個のd次元ベクトル{y1,y2,…,ym}を取得する取得手段と、
カーネル関数値k(yi,yj)を第ij成分とするm×m行列をKyとし、カーネル関数値k(xi,yj)を第ij成分とするn×m行列をKxyとして、一般化固有値問題KxyTKxyz=λKyz、又は、正則化一般化固有値問題KxyTKxy(KxyTKxy+μKy)KxyTKxyz=λKyzを解くことによって、r個の固有ベクトル{z1,z2,…,zr}を算出する設計手段と、
上記r個の固有ベクトル{z1,z2,…,zr}を用いて、上記d次元ベクトルxを上記r次元ベクトルyに変換する評価手段と、とを備えている、
ことを特徴とするカーネル主成分分析装置。
【請求項8】
コンピュータを請求項7に記載のカーネル主成分分析装置として動作させるためのためのカーネル主成分分析プログラムであって、上記コンピュータを上記カーネル主成分分析装置が備えている各手段として機能させるカーネル主成分分析プログラム。
【図1】


【図2】


【図3】


【図4】


【図5】


【図6】


【図7】


【図8】


【図9】


【図10】


【図11】




【図2】


【図3】


【図4】


【図5】


【図6】


【図7】


【図8】


【図9】


【図10】


【図11】


【公開番号】特開2011−22912(P2011−22912A)
【公開日】平成23年2月3日(2011.2.3)
【国際特許分類】
【出願番号】特願2009−169072(P2009−169072)
【出願日】平成21年7月17日(2009.7.17)
【出願人】(503359821)独立行政法人理化学研究所 (1,056)
【Fターム(参考)】
【公開日】平成23年2月3日(2011.2.3)
【国際特許分類】
【出願日】平成21年7月17日(2009.7.17)
【出願人】(503359821)独立行政法人理化学研究所 (1,056)
【Fターム(参考)】
[ Back to top ]

